Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T23:44:28.833Z Has data issue: false hasContentIssue false
  • English
  • Français

ON VALUES TAKEN BY THE LARGEST PRIME FACTOR OF SHIFTED PRIMES

Part of: Multiplicative number theory

Published online by Cambridge University Press:  15 August 2018

JIE WU
JIE WU*
Affiliation:
Department of Mathematics, Southwest University, 2 Tiansheng Road, Beibei, 400715 Chongqing, China CNRS UMR 8050, Laboratoire d’Analyse et de Mathématiques Appliquées, Université Paris-Est Créteil, 61 avenue du Général de Gaulle, 94010 Créteil Cedex, France email jie.wu@math.cnrs.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Denote by 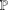$\mathbb{P}$ the set of all prime numbers and by 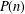$P(n)$ the largest prime factor of positive integer 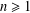$n\geq 1$ with the convention 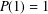$P(1)=1$. In this paper, we prove that, for each 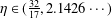$\unicode[STIX]{x1D702}\in (\frac{32}{17},2.1426\cdots \,)$, there is a constant 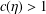$c(\unicode[STIX]{x1D702})>1$ such that, for every fixed nonzero integer 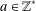$a\in \mathbb{Z}^{\ast }$, the set

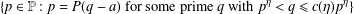$$\begin{eqnarray}\{p\in \mathbb{P}:p=P(q-a)\text{ for some prime }q\text{ with }p^{\unicode[STIX]{x1D702}}<q\leq c(\unicode[STIX]{x1D702})p^{\unicode[STIX]{x1D702}}\}\end{eqnarray}$$
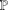has relative asymptotic density one in $\mathbb{P}$. This improves a similar result due to Banks and Shparlinski [‘On values taken by the largest prime factor of shifted primes’, J. Aust. Math. Soc.82 (2015), 133–147], Theorem 1.1, which requires 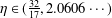$\unicode[STIX]{x1D702}\in (\frac{32}{17},2.0606\cdots \,)$ in place of 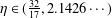$\unicode[STIX]{x1D702}\in (\frac{32}{17},2.1426\cdots \,)$.

Keywords

shifted primefriable integersieve

MSC classification

Primary: 11N05: Distribution of primes
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 1 , August 2019 , pp. 133 - 144
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The author is supported in part by NSFC (grant no. 11771121).

References

Baker, R. C. and Harman,  G., ‘The Brun–Titchmarsh theorem on average’, in: Analytic Number Theory, Vol. 1 (Allerton Park, IL, 1995), Progress in Mathematics, 138 (Birkhäuser, Boston, MA, 1996), 39–103.Google Scholar
Banks, W. and Shparlinski, I. E., ‘On values taken by the largest prime factor of shifted primes’, J. Aust. Math. Soc. 82 (2015), 133–147.Google Scholar
Chen, J.-R., ‘On the representation of a large even integer as the sum of a prime and the product of at most two primes’, Sci. Sinica 16 (1973), 157–176.Google Scholar
Chen, F.-J. and Chen, Y.-G., On the largest prime factor of shifted primes, Acta Math. Sinica, English Series, August 15, 2016.Google Scholar
Feng, B. and Wu, J., ‘On the density of shifted primes with large prime factors’, Sci. China Math. 61(1) (2018), 83–94.Google Scholar
Fouvry, É., ‘Théorème de Brun-Titichmarsh; application au théorème de Fermat’, Invent. Math. 79 (1985), 383–407.Google Scholar
Goldfeld, M., ‘On the number of primes p for which p + a has a large prime factor’, Mathematika 16 (1969), 23–27.Google Scholar
Iwaniec, H., ‘Primes of the type 𝜙(x, y) + A where 𝜙 is a quadratic form’, Acta Arith. 21 (1972), 203–234.Google Scholar
Iwaniec, H., ‘Rosser’s sieve’, Acta Arith. 36 (1980), 171–202.Google Scholar
Iwaniec, H., ‘A new form of the error term in the linear sieve’, Acta Arith. 37 (1980), 307–320.Google Scholar
Liu, J.-Y., Wu, J. and Xi, P., Primes in arithmetic progressions with friable indices, Preprint, 2017.Google Scholar
Luca, F., Menares, R. and Pizarro-Madariaga, A., ‘On shifted primes with large prime factors and their products’, Bull. Belg. Math. Soc. Simon Stevin 22 (2015), 39–47.Google Scholar
Motohashi, Y., ‘An induction principle for the generalization of Bombieri’s prime number theorem’, Proc. Japan Acad. 52 (1976), 273–275.Google Scholar
Rivest, R. and Silverman, R., Are ‘Strong’ Primes Needed for RSA? Cryptology ePrint Archive: Report 2001/007, http://eprint.iacr.org/2001/007.Google Scholar
Tenenbaum, G., Introduction to Analytic and Probabilistic Number Theory, Cambridge Studies in Advanced Mathematics, 46 (ed. Thomas, C. B.) (Cambridge University Press, Cambridge, 1995), xvi+448 pp. Translated from the second French edition (1995).Google Scholar
Vishnoi, N. K., Theoretical aspects of randomization in computation, PhD Thesis, Georgia Inst. of Technology, 2004 (http://smartech.gatech.edu:8282/dspace/handle/1853/5049).Google Scholar
Zhang, Y., ‘Bounded gaps between primes’, Ann. of Math. (2) 179 (2014), 1121–1174.Google Scholar