Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kuhn, M. Gabriella
and
Steger, Tim
2010.
Size of matrix coefficients characterizes anisotropic principal series representations of the free group.
Monatshefte für Mathematik,
Vol. 160,
Issue. 2,
p.
151.

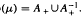 . Let λ be an endpoint of the spectrum of μ considered as a convolver on ℓ
. Let λ be an endpoint of the spectrum of μ considered as a convolver on ℓ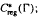 in particular, Paschke's conjecture holds for λ − μ.
in particular, Paschke's conjecture holds for λ − μ.