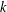Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T10:18:59.643Z Has data issue: false hasContentIssue false
  • English
  • Français

PERIODIC $k$-GRAPH ALGEBRAS REVISITED

Part of: Selfadjoint operator algebras Linear spaces and algebras of operators

Published online by Cambridge University Press:  20 April 2015

DILIAN YANG
DILIAN YANG*
Affiliation:
Department of Mathematics and Statistics, University of Windsor, Windsor, Ontario, CanadaN9B 3P4 email dyang@uwindsor.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 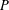$P$ be a finitely generated cancellative abelian monoid. A 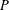$P$-graph 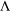${\rm\Lambda}$ is a natural generalization of a 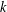$k$-graph. A pullback of 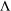${\rm\Lambda}$ is constructed by pulling it back over a given monoid morphism to 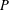$P$, while a pushout of 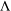${\rm\Lambda}$ is obtained by modding out its periodicity, which is deduced from a natural equivalence relation on 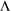${\rm\Lambda}$. One of our main results in this paper shows that, for some 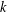$k$-graphs 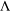${\rm\Lambda}$, 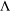${\rm\Lambda}$ is isomorphic to the pullback of its pushout via a natural quotient map, and that its graph 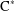$\text{C}^{\ast }$-algebra can be embedded into the tensor product of the graph 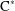$\text{C}^{\ast }$-algebra of its pushout and 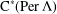$\text{C}^{\ast }(\text{Per}\,{\rm\Lambda})$. As a consequence, in this case, the cycline algebra generated by the standard generators corresponding to equivalent pairs is a maximal abelian subalgebra, and there is a faithful conditional expectation from the graph 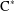$\text{C}^{\ast }$-algebra onto it.

Keywords

k-graphP-graphpullbackpushoutperiodicitymaximal abelian subalgebra

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 47L30: Abstract operator algebras on Hilbert spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 99 , Issue 2 , October 2015 , pp. 267 - 286
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Brown, J., Nagy, G. and Reznikoff, S., ‘A generalized Cuntz–Krieger uniqueness theorem for higher-rank graphs’, J. Funct. Anal. 266 (2014), 2590–2609.CrossRefGoogle Scholar
Carlsen, T. M., Kang, S., Shotwell, J. and Sims, A., ‘The primitive ideals of the Cuntz–Krieger algebra of a row-finite higher-rank graph with no sources’, J. Funct. Anal. 266 (2014), 2570–2589.CrossRefGoogle Scholar
Davidson, K. R. and Yang, D., ‘Periodicity in rank 2 graph algebras’, Canad. J. Math. 61 (2009), 1239–1261.CrossRefGoogle Scholar
Davidson, K. R. and Yang, D., ‘Representations of higher rank graph algebras’, New York J. Math. 15 (2009), 169–198.Google Scholar
Hong, J. H. and Szymański, W., ‘The primitive ideal space of the C∗ -algebras of infinite graphs’, J. Math. Soc. Japan 56 (2004), 45–64.Google Scholar
Hopenwasser, A., ‘The spectral theorem for bimodules in higher rank graph C∗ -algebras’, Illinois J. Math. 49 (2005), 993–1000.CrossRefGoogle Scholar
an Huef, A., Laca, M., Raeburn, I. and Sims, A., ‘KMS states on the C∗ -algebra of a higher-rank graph and periodicity in the path space’, J. Funct. Anal. 268 (2015), 1840–1875.CrossRefGoogle Scholar
Kang, S. and Pask, D., ‘Aperiodicity and the primitive ideal space of a row-finite higher rank graph C∗ -algebra’, Internat. J. Math. 25 (2014), 1450022.CrossRefGoogle Scholar
Kumjian, A. and Pask, D., ‘Higher rank graph C* -algebras’, New York J. Math. 6 (2000), 1–20.Google Scholar
Lewin, P. and Sims, A., ‘Aperiodicity and cofinality for finitely aligned higher-rank graphs’, Math. Proc. Cambridge Philos. Soc. 149 (2010), 333–350.CrossRefGoogle Scholar
Nagy, G. and Reznikoff, S., ‘Abelian core of graph algebras’, J. Lond. Math. Soc. (2) 85 (2012), 889–908.CrossRefGoogle Scholar
Raeburn, I., Graph Algebras, CBMS 103 (American Mathematical Society, Providence, RI, 2005).CrossRefGoogle Scholar
Robertson, D. I. and Sims, A., ‘Simplicity of C∗ -algebras associated to higher-rank graphs’, Bull. Lond. Math. Soc. 39 (2007), 337–344.CrossRefGoogle Scholar
Rosales, J. C. and García-Sánchez, P. A., Finitely Generated Commutative Monoids (Nova Publishers, Commack, NY, 1999).Google Scholar
Shotwell, J., ‘Simplicity of finitely aligned k-graph C∗ -algebras’, J. Operator Theory 67 (2012), 335–347.Google Scholar
Wassermann, S., ‘The slice map problem for C∗ -algebras’, Proc. Lond. Math. Soc. (3) 32 (1976), 537–559.CrossRefGoogle Scholar
Wassermann, S., ‘Tensor products of maximal abelian subalgebras of C∗ -algebras’, Glasg. Math. J. 50 (2008), 209–216.CrossRefGoogle Scholar