Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T16:47:49.819Z Has data issue: false hasContentIssue false
  • English
  • Français

PERTURBATION THEOREMS FOR FRACTIONAL CRITICAL EQUATIONS ON BOUNDED DOMAINS

Part of: Elliptic equations and systems

Published online by Cambridge University Press:  09 March 2020

AZEB ALGHANEMI  and
HICHEM CHTIOUI Open the ORCID record for HICHEM CHTIOUI [Opens in a new window]
AZEB ALGHANEMI
Affiliation:
Department of Mathematics, King Abdulaziz University, P.O. Box 80230, Jeddah, Kingdom of Saudi Arabia e-mail: aalghanemi@kau.edu.sa
HICHEM CHTIOUI
Affiliation:
Department of Mathematics, Sfax University, Faculty of Sciences of Sfax, 3018 Sfax, Tunisia e-mail: Hichem.Chtioui@fss.rnu.tn
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the fractional critical problem 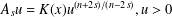$A_{s}u=K(x)u^{(n+2s)/(n-2s)},u>0$ in 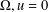$\unicode[STIX]{x1D6FA},u=0$ on 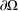$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$, where 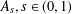$A_{s},s\in (0,1)$, is the fractional Laplace operator and 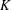$K$ is a given function on a bounded domain $\unicode[STIX]{x1D6FA}$ of 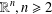$\mathbb{R}^{n},n\geq 2$. This is based on A. Bahri’s theory of critical points at infinity in Bahri [Critical Points at Infinity in Some Variational Problems, Pitman Research Notes in Mathematics Series, 182 (Longman Scientific & Technical, Harlow, 1989)]. We prove Bahri’s estimates in the fractional setting and we provide existence theorems for the problem when 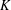$K$ is close to 1.

Keywords

fractional Laplace operatorcritical equation

MSC classification

Primary: 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 2 , October 2021 , pp. 159 - 178
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by F. Cirstea

This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia under Grant No. (KEP-PhD-41-130-38). The authors, therefore, acknowledge with thanks DSR technical and financial support.

References

Bahri, A., Critical Points at Infinity in Some Variational Problems, Pitman Research Notes in Mathematics Series, 182 (Longman Scientific & Technical, Harlow, 1989).Google Scholar
Bahri, A., ‘An invariant for Yamabe-type flows with applications to scalar curvature problems in high dimensions’, Duke Math. J. 81 (1996), 323–466.Google Scholar
Bahri, A. and Rabinowitz, P., ‘Periodic orbits of hamiltonian systems of three body type’, Ann. Inst. H. Poincaré Anal. Non Linéaire 8 (1991), 561–649.Google Scholar
Ben Mahmoud, R. and Chtioui, H., ‘Prescribing the scalar curvature problem on higher-dimensional manifolds’, Discrete Contin. Dyn. Syst. 32(5) (2012), 1857–1879.Google Scholar
Brändle, C., Colorado, E., de Pablo, A. and Sánchez, U., ‘A concave-convex elliptic problem involving the fractional Laplacian’, Proc. R. Soc. Edinburgh Sect. A 143 (2013), 39–71.Google Scholar
Chang, A. and Gonzalez, M., ‘Fractional Laplacian in conformal geometry’, Adv. Math. 226(2) (2011), 1410–1432.Google Scholar
Chtioui, H. and Abdelhedi, W., ‘On a fractional Nirenberg problem on n-dimensional spheres: existence and multiplicity results’, Bull. Sci. Math. 140(6) (2016), 617–628.Google Scholar
Chtioui, H., Abdelhedi, W. and Hajaiej, H., ‘A complete study of the lack of compactness and existence results of a fractional Nirenberg equation via a flatness hypothesis: Part I’, Anal. PDE 9(6) (2016), 1285–1315.Google Scholar
Chtioui, H., Abdelhedi, W. and Hajaiej, H., ‘The Bahri–Coron theorem for fractional Yamabe-type problems’, Adv. Nonlinear Stud. 18(2) (2018), 393–407.Google Scholar
Coron, J. M. and Bahri, A., ‘On a nonlinear elliptic equation involving the critical Sobolev exponent: the effect of topology of the domain’, Comm. Pure Appl. Math. 41 (1988), 255–294.Google Scholar
Li, Y., Jin, T. and Xiong, J., ‘On a fractional Nirenberg problem, part I: Blow up analysis and compactness of solutions’, J. Eur. Math. Soc. (JEMS) 16 (2014), 1111–1171.Google Scholar
Li, Y., Jin, T. and Xiong, J., ‘On a fractional Nirenberg problem, part II: Existence of solutions’, Int. Math. Res. Not. IMRN (6) 2015 (2015), 1555–1589.Google Scholar
Li, Y., Jin, T. and Xiong, J., ‘The Nirenberg problem and its generalizations: a unified approach’, Math. Ann. 369(1–2) (2017), 109–151.Google Scholar
Palatucci, J., Di Nezza, E. and Valdinoci, E., ‘Hitchhiker’s guide to the fractional Sobolev spaces’, Bull. Sci. Math. 136 (2012), 521–573.Google Scholar
Sharaf, K., ‘An infinite number of solutions for an elliptic problem with power nonlinearity’, Differential Integral Equations 30 (2017), 133–144.Google Scholar
Silvestre, L. and Caffarelli, L., ‘An extension problem related to the fractional Laplacian’, Comm. Partial Differential Equations 32 (2007), 1245–1260.Google Scholar
Struwe, M., ‘A global compactness result for elliptic boundary value problem involving limiting nonlinearities’, Math. Z. 187 (1984), 511–517.Google Scholar
Tan, J., ‘Positive solutions of nonlinear problems involving the square root of the Laplacian’, Adv. Math. 224 (2010), 2052–2093.Google Scholar
Tan, J., ‘The Brezis–Nirenberg type problem involving the square root of the Laplacian’, Calc. Var. Partial Differential Equations 42 (2011), 21–41.Google Scholar
Tan, J., ‘Positive solutions for non local elliptic problems’, Discrete Contin. Dyn. Syst. 33 (2013), 837–859.Google Scholar
Tavoularis, N. and Cotsiolis, A., ‘Best constants for Sobolev inequalities for higher order fractional derivatives’, J. Math. Anal. Appl. 295 (2004), 225–236.Google Scholar
Torrea, J. and Stinga, P., ‘Extension problem and Harnack’s inequality for some fractional operators’, Comm. Partial Differential Equations 35 (2010), 2092–2122.Google Scholar
Zheng, Y., Chen, Y. and Liu, C., ‘Existence results for the fractional Nirenberg problem’, J. Funct. Anal. 270(11) (2016), 4043–4086.Google Scholar