Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-11T03:58:44.457Z Has data issue: false hasContentIssue false
  • English
  • Français

Posets and differential graded algebras

Part of: Ordered sets

Published online by Cambridge University Press:  09 April 2009

Jacqui Ramagge  and
Wayne W. Wheeler
Jacqui Ramagge
Affiliation:
Mathematics Department University of NewcastleNSW 2308Australia e-mail: jacqui@maths.newcastle.edu.au
Wayne W. Wheeler
Affiliation:
Department of Mathematics University of GeorgiaAthens, GA 30602USA e-mail: www@alpha.math.uga.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If P is a partially ordered set and R is a commutative ring, then a certain differential graded R-algebra A•(P) is defined from the order relation on P. The algebra A•(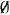) corresponding to the empty poset is always contained in A•(P) so that A•(P) can be regarded as an A•(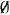)-algebra. The main result of this paper shows that if R is an integral domain and P and P′ are finite posets such that A•(P)≅A•(P′) as differential graded A•(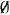)-algebras, then P and P′ are isomorphic.

MSC classification

Secondary: 06A06: Partial order, general
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 64 , Issue 1 , February 1998 , pp. 1 - 19
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Bruns, W. and Herzog, J.. Cohen–Macaulay rings (Cambridge Univ. Press, Cambridge, 1993).Google Scholar
[2]Simpson, D., Linear representations of partially ordered sets and vector space categories (Gordon and Breach, Amsterdam, 1992).Google Scholar
[3]Stanley, R., ‘Cohen–Macaulay complexes’, in: Higher combinatorics (ed. Aigner, M.) (Reidel, Dordrecht, 1977) pp.51–62.CrossRefGoogle Scholar