Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T17:37:28.664Z Has data issue: false hasContentIssue false
  • English
  • Français

A problem on rough parametric Marcinkiewicz functions

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  09 April 2009

Yong Ding ,
Shanzhen Lu  and
Kôzô Yabuta
Yong Ding
Affiliation:
Department of Mathematics, Beijing Normal University, Beijing, 100875, P. R., China e-mail: dingy@bnu.edu.cn e-mail: lusz@bnu.edu.cn
Shanzhen Lu
Affiliation:
Department of Mathematics, Beijing Normal University, Beijing, 100875, P. R., China e-mail: dingy@bnu.edu.cn e-mail: lusz@bnu.edu.cn
Kôzô Yabuta
Affiliation:
School of Science, Kwansei Gakuin University, Uegahara 1-1-155, Nishinomiya 662-8501Japan e-mail: yabuta@kwansei.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

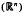
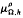In this note the authors give the L2(n) boundedness of a class of parametric Marcinkiewicz integral with kernel function Ω in 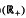L log+L(Sn−1) and radial function h(|x|) ∈ l ∞ l(Lq)(+) for 1 < q ≦.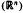

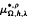As its corollary, the Lp (n)(2 < p < ∞) boundedness of and and 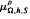with Ω in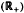 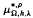L log+L (Sn-1) and h(|x|) ∈ l∞ (Lq)(+) are also obtained. Here and 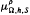are parametric Marcinkiewicz functions corresponding to the Littlewood-Paley g*λ-function and the Lusin area function S, respectively.

Keywords

Marcinkiewicz integralLittlewood-Paley g-functionLusin area integralrough kernel

MSC classification

Secondary: 42B25: Maximal functions, Littlewood-Paley theory 42B99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 72 , Issue 1 , February 2002 , pp. 13 - 22
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Benedek, A., Calderón, A. and Panzone, R., ‘Convolution operators on Banach space valued functions’, Proc. Nat. Acad. Sci. USA 48 (1962), 356–365.CrossRefGoogle ScholarPubMed
[2]Calderón, A. and Zygmund, A., ‘A note on the interpolation of sublinear operators’, Amer. J. Math. 78 (1956), 282–288.CrossRefGoogle Scholar
[3]Duoandikoetxea, J. and Rubio de Francia, J. L., ‘Maximal and singular integral operators via Fourier transform estimates’, Invent. Math. 84 (1986), 541–561.CrossRefGoogle Scholar
[4]Fan, D. and Sato, S., ‘Weak type (1, 1) estimates for Marcinkiewicz integrals with rough kernels’, Tôhoku Math. J., to appear.Google Scholar
[5]Hörmander, L., ‘Translation invariant operators’, Acta Math. 104 (1960), 93–139.CrossRefGoogle Scholar
[6]Sakamoto, M. and Yabuta, K., ‘Boundedness of Marcinkiewicz functions’, Studia Math. 135 (1999), 103–142.Google Scholar
[7]Stein, E. M., ‘On the functions of Littlewood-Paley, Lusin and Marcinkiewicz’, Trans. Amer. Math. Soc. 88 (1958), 430–466.CrossRefGoogle Scholar
[8]Sun, Q., ‘Two problems about singular integral operators’, Approx. Theory Appl. 7 (1991), 83–98.Google Scholar
[9]Torchinsky, A. and Wang, S., ‘A note on the Marcinkiewicz integral’, Coll. Mat. 61–62 (1990), 235–243.CrossRefGoogle Scholar