Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gilman, Jane
2008.
The structure of two-parabolic space: parabolic dust and iteration.
Geometriae Dedicata,
Vol. 131,
Issue. 1,
p.
27.
Gutan, Marin
2014.
Diophantine Equations and the Freeness of Möbius Groups.
Applied Mathematics,
Vol. 05,
Issue. 10,
p.
1400.
Akiyoshi, Hirotaka
Ohshika, Ken’ichi
Parker, John
Sakuma, Makoto
and
Yoshida, Han
2021.
Classification of non-free Kleinian groups generated by two parabolic transformations.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 3,
p.
1765.
Smilga, Ilia
2021.
New sequences of non-free rational points.
Comptes Rendus. Mathématique,
Vol. 359,
Issue. 8,
p.
983.
Jang, Wonyong
and
Kim, KyeongRo
2021.
A sequence of algebraic integer relation numbers which converges to 4.
Topology and its Applications,
Vol. 294,
Issue. ,
p.
107665.
Kim, Sang-hyun
and
Koberda, Thomas
2022.
Non-freeness of Groups Generated by Two Parabolic Elements with Small Rational Parameters.
Michigan Mathematical Journal,
Vol. 71,
Issue. 4,
Choi, Philip
Jo, Kyeonghee
Kim, Hyuk
and
Lee, Junho
2025.
Non-freeness of parabolic two-generator groups.
International Journal of Mathematics,
Vol. 36,
Issue. 05,

 is not free by using quadratic Diophantine equations of the form ax
is not free by using quadratic Diophantine equations of the form ax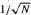 are accumulation points, where
are accumulation points, where 