Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T01:31:43.936Z Has data issue: false hasContentIssue false
  • English
  • Français

THE QUOTIENT ALGEBRA OF COMPACT-BY-APPROXIMABLE OPERATORS ON BANACH SPACES FAILING THE APPROXIMATION PROPERTY

Part of: Normed linear spaces and Banach spaces; Banach lattices Linear spaces and algebras of operators

Published online by Cambridge University Press:  07 June 2019

HANS-OLAV TYLLI  and
HENRIK WIRZENIUS
HANS-OLAV TYLLI*
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, Box 68, Pietari Kalmin katu 5, FI-00014Helsinki, Finland
HENRIK WIRZENIUS
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, Box 68, Pietari Kalmin katu 5, FI-00014Helsinki, Finland e-mail: henrik.wirzenius@helsinki.fi
*
e-mail: hans-olav.tylli@helsinki.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

We initiate a study of structural properties of the quotient algebra 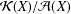${\mathcal{K}}(X)/{\mathcal{A}}(X)$ of the compact-by-approximable operators on Banach spaces 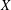$X$ failing the approximation property. Our main results and examples include the following: (i) there is a linear isomorphic embedding from 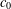$c_{0}$ into 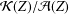${\mathcal{K}}(Z)/{\mathcal{A}}(Z)$, where 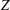$Z$ belongs to the class of Banach spaces constructed by Willis that have the metric compact approximation property but fail the approximation property, (ii) there is a linear isomorphic embedding from a nonseparable space 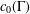$c_{0}(\unicode[STIX]{x1D6E4})$ into 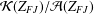${\mathcal{K}}(Z_{FJ})/{\mathcal{A}}(Z_{FJ})$, where 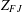$Z_{FJ}$ is a universal compact factorisation space arising from the work of Johnson and Figiel.

Keywords

quotient algebracompact-by-approximable operatorsapproximation properties

MSC classification

Primary: 46B28: Spaces of operators; tensor products; approximation properties 47L10: Algebras of operators on Banach spaces and other topological linear spaces
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 110 , Issue 2 , April 2021 , pp. 266 - 288
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by A. Sims

H. Wirzenius gratefully acknowledges the financial support of The Swedish Cultural Foundation in Finland and the Magnus Ehrnrooth Foundation.

References

Alexander, F. E., ‘Compact and finite rank operators on subspaces of ℓ p’, Bull. Lond. Math. Soc. 6 (1974), 341–342.CrossRefGoogle Scholar
Argyros, S. and Haydon, R. G., ‘A hereditarily indecomposable L ∞-space that solves the scalar-plus-compact problem’, Acta Math. 206 (2011), 1–54.CrossRefGoogle Scholar
Aron, R., Lindström, M., Ruess, W. M. and Ryan, R., ‘Uniform factorization for compact operators’, Proc. Amer. Math. Soc. 127 (1999), 1119–1125.CrossRefGoogle Scholar
Bachelis, G. F., ‘A factorization theorem for compact operators’, Illinois J. Math. 20 (1976), 626–629.CrossRefGoogle Scholar
Caradus, S. R., Pfaffenberger, W. E. and Yood, B., Calkin Algebras and Algebras of Operators on Banach Spaces, Lecture Notes in Pure and Applied Mathematics, 9 (Marcel Dekker, New York, 1974).Google Scholar
Carl, B. and Stephani, I., Entropy, Compactness and the Approximation of Operators (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Casazza, P. G., ‘Approximation properties’, in: Handbook of the Geometry of Banach Spaces, Vol. 1 (eds. Johnson, W. B. and Lindenstrauss, J.) (North-Holland–Elsevier, Amsterdam, 2001), Ch. 7, 271–316.CrossRefGoogle Scholar
Casazza, P. G. and Jarchow, H., ‘Self-induced compactness in Banach spaces’, Proc. Roy. Soc. Edinburgh Sect. A 126 (1996), 355–362.CrossRefGoogle Scholar
Dales, H. G., Banach Algebras and Automatic Continuity (Oxford University Press, Oxford, 2000).Google Scholar
Dales, H. G., ‘A Banach algebra related to a Banach space without AP’, Notes, 2013.Google Scholar
Enflo, P., ‘A counterexample to the approximation property in Banach spaces’, Acta Math. 139 (1973), 309–317.CrossRefGoogle Scholar
Fabian, M., Habala, P., Hajek, P., Montesinos, V. and Zizler, V., Banach Space Theory, CMS Books in Mathematics (Springer, New York, 2011).CrossRefGoogle Scholar
Figiel, T., ‘Factorization of compact operators and applications to the approximation problem’, Studia Math. 45 (1973), 191–210.CrossRefGoogle Scholar
Freeman, D., Schlumprecht, T. and Zsák, A., ‘Closed ideals of operators between classical sequence spaces’, Bull. Lond. Math. Soc. 49 (2017), 859–876.CrossRefGoogle Scholar
Godefroy, G. and Saphar, P. D., ‘Three-space problems for the approximation properties’, Proc. Amer. Math. Soc. 105 (1989), 70–75.CrossRefGoogle Scholar
Grabiner, S., ‘The nilpotency of Banach nil algebras’, Proc. Amer. Math. Soc. 21 (1969), 510.Google Scholar
John, K., ‘On the compact nonnuclear operator problem’, Math. Ann. 287 (1990), 509–514.CrossRefGoogle Scholar
Johnson, W. B., ‘Factoring compact operators’, Israel J. Math. 9 (1971), 337–345.CrossRefGoogle Scholar
Johnson, W. B., ‘A complementably universal conjugate Banach space and its relation to the approximation problem’, Israel J. Math. 13 (1972), 301–310.CrossRefGoogle Scholar
Johnson, W. B., Pisier, G. and Schechtman, G., ‘Ideals in $L(L_{1})$’, Preprint, 2018, arXiv:1811.06571.Google Scholar
Kania, T. and Laustsen, N. J., ‘Ideal structure of the algebra of bounded operators acting on a Banach space’, Indiana Univ. Math. J. 66 (2017), 1019–1043.CrossRefGoogle Scholar
Kürsten, K.-D. and Pietsch, A., ‘Non-approximable compact operators’, Arch. Math. 103 (2014), 473–480.CrossRefGoogle Scholar
Leung, D. H., ‘Some stability properties of c 0 -saturated spaces’, Math. Proc. Cambridge Philos. Soc. 118 (1995), 287–301.CrossRefGoogle Scholar
Lima, Å. and Oja, E., ‘Ideals of compact operators’, J. Aust. Math. Soc. 77 (2004), 91–110.CrossRefGoogle Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. Sequence Spaces, Ergebnisse der Mathematik, 92 (Springer, Berlin, 1977).Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. Function Spaces, Ergebnisse der Mathematik, 97 (Springer, Berlin, 1979).CrossRefGoogle Scholar
Mikkor, K. and Oja, E., ‘Uniform factorization for compact sets of weakly compact operators’, Studia Math. 174 (2006), 85–97.CrossRefGoogle Scholar
Motakis, P., Puglisi, D. and Zisimopoulou, D., ‘A hierarchy of Banach spaces with C (K) Calkin algebras’, Indiana Univ. Math. J. 65 (2016), 39–67.CrossRefGoogle Scholar
Murphy, G. J., C∗ -Algebras and Operator Theory (Academic Press, Boston, MA, 1990).Google Scholar
Oikhberg, T. and Spinu, E., ‘Subprojective Banach spaces’, J. Math. Anal. Appl. 424 (2015), 613–625.CrossRefGoogle Scholar
Oja, E., ‘Lifting bounded approximation properties from Banach spaces to their dual spaces’, J. Math. Anal. Appl. 323 (2006), 666–679.CrossRefGoogle Scholar
Oja, E. and Zolk, I., ‘On commuting approximation properties of Banach spaces’, Proc. Roy. Soc. Edinburgh Sect. A 139 (2009), 551–565.CrossRefGoogle Scholar
Palmer, T. W., Banach Algebras and the General Theory of ∗ -Algebras. Vol. I: Algebras and Banach Algebras, Encyclopedia of Mathematics and its Applications, 49 (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar
Pietsch, A., Operator Ideals (North-Holland, Amsterdam, 1980).Google Scholar
Pisier, G., ‘Counterexamples to a conjecture of Grothendieck’, Acta Math. 151 (1983), 181–208.CrossRefGoogle Scholar
Pisier, G., Factorization of Linear Operators and Geometry of Banach Spaces, Conference Board of the Mathematical Sciences Series, 60 (American Mathematical Society, Providence, RI, 1986).CrossRefGoogle Scholar
Schlumprecht, T. and Zsák, A., ‘The algebra of bounded linear operators on ℓ p⊕ℓ q has infinitely many closed ideals’, J. reine angew. Math. 735 (2018), 225–247.CrossRefGoogle Scholar
Szankowski, A., ‘Subspaces without the approximation property’, Israel J. Math. 30 (1978), 123–129.CrossRefGoogle Scholar
Szankowski, A., ‘𝓑(H) does not have the approximation property’, Acta Math. 147 (1981), 89–108.CrossRefGoogle Scholar
Tarbard, M., ‘Hereditarily indecomposable, separable 𝓛∞ Banach space with ℓ 1 dual having few but not very few operators’, J. Lond. Math. Soc. 85 (2012), 737–764.CrossRefGoogle Scholar
Tylli, H.-O., ‘The essential norm of an operator is not self-dual’, Israel J. Math. 91 (1995), 93–110.CrossRefGoogle Scholar
Willis, G., ‘The compact approximation property does not imply the approximation property’, Studia Math. 103 (1992), 99–108.CrossRefGoogle Scholar