Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T07:24:37.060Z Has data issue: false hasContentIssue false
  • English
  • Français

Radical Theory for Granded Rings

Published online by Cambridge University Press:  09 April 2009

Honghin Fang  and
Patrick Stewart
Honghin Fang
Affiliation:
Yangzhou Teacher's CollegeYangzhou, Jiangsu People's Republic of, China
Patrick Stewart
Affiliation:
Dalhousie UniversityHalifax, Nova ScotiaCanadaB3H 3J5
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we propose a general setting in which to study the radical theory of group graded rings. If 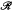is a radical class of associative rings we consider two associated radical classes of graded rings which are denoted by 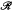G and 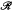ref. We show that if 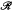is special (respectively, normal), then both 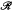G and 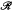ref are graded special (respectively, graded normal). Also, we discuss a graded version of the ADS theorem and the termination of the Kurosh lower graded radical construction.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 52 , Issue 2 , April 1992 , pp. 143 - 153
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Beattie, M., ‘A generalization of the smash product of a graded ring,’ J. Pure Appl Algebra 52 (1988), 219–226.CrossRefGoogle Scholar
[2]Beattie, M. and Stewart, P., ‘Graded radicals of graded rings,’ Acta Math. Acad. Sci. Hungar, to appear.Google Scholar
[3]Beattie, M., S.-X., Liu, and Stewart, P., ‘Comparing graded versions of the prime radical,’ Canad. Math. Bull., to appear.Google Scholar
[4]Beattie, M. and Stewart, P., ‘Graded versions of radicals,’ Proc. of the II SBWAG Conference, Santiago 1989, 17–22.Google Scholar
[5]Bergman, O., ‘On Jacobson radicals of graded rings,’ preprint.Google Scholar
[6]Cohen, M. and Montgomery, S., ‘Group graded rings, smash products and group actions,’ Trans. Amer. Math. Soc. 282 (1984), 237–258.Google Scholar
[7]Gardner, B. J. and Stewart, P. N., ‘On semisimple radical classes,’ Bull. Austral. Math. Soc. 13 (1975), 349–353.Google Scholar
[8]Jaegermann, M., ‘Normal radicals,’ Fund. Math. 95 (1977), 147–155.CrossRefGoogle Scholar
[9]Krempa, J. and Terlikowska-Oslowska, B., ‘On graded radical theory,’ Warsaw, 1987, preprint.Google Scholar
[10]Nastasescu, C. and Van Oystaeyen, F., ‘The strongly prime radical of graded rings,’ Bull. Soc. Math. Belg. Sér. B 36 (1984), 243–251.Google Scholar
[11]Puczylowski, E. R., ‘On general theory of radicals,’ preprint.Google Scholar
[12]Sands, A. D., ‘On normal radicals,’ J. London Math. Soc. (2) 11 (1975), 361–365.Google Scholar
[13]Sulinski, A. and Wiegandt, R., ‘Radicals of rings graded by abelian groups’, Colloq. Math. Soc. J´nos Bolyai 38 (1982), 607–6 17.Google Scholar
[14]Szasz, F. A., Radicals of rings, (Akadémiai Kiadó, Budapest, 1981).Google Scholar