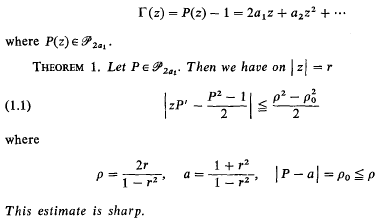Published online by Cambridge University Press: 09 April 2009
Letp denote the family of functions  regular in E{z:|z| < 1} and with positive real part there. We propose to study, in this article, the subclass p2a1 of p whose functions P(z) have pre-assigned second coefficient 2a1. In what follows we may assume, without loss in generality, that a1 is real and non-negative. This assumption will be made throughout. As is well known [2], 0 ≦ a1 ≦ 1. In Theorem 1 we derive a generalization of Zmorovic's theorem 1, [3]. determine the radius of univalence and starlikeness of the class of functions
regular in E{z:|z| < 1} and with positive real part there. We propose to study, in this article, the subclass p2a1 of p whose functions P(z) have pre-assigned second coefficient 2a1. In what follows we may assume, without loss in generality, that a1 is real and non-negative. This assumption will be made throughout. As is well known [2], 0 ≦ a1 ≦ 1. In Theorem 1 we derive a generalization of Zmorovic's theorem 1, [3]. determine the radius of univalence and starlikeness of the class of functions