Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mashreghi, Javad
2023.
Lectures on Analytic Function Spaces and their Applications.
Vol. 39,
Issue. ,
p.
1.
Hai Khoi, Le
and
Mashreghi, Javad
2023.
Theory of Np Spaces.
p.
27.
Xie, Huayou
Liu, Junming
and
Ponnusamy, Saminathan
2023.
Volterra-type operators on the minimal Möbius-invariant space.
Canadian Mathematical Bulletin,
Vol. 66,
Issue. 2,
p.
509.


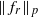 as
as 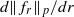 grows at most like
grows at most like 