Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T14:56:01.514Z Has data issue: false hasContentIssue false
  • English
  • Français

REAL THETA CHARACTERISTICS AND AUTOMORPHISMS OF A REAL CURVE

Published online by Cambridge University Press:  22 January 2010

INDRANIL BISWAS  and
SIDDHARTHA GADGIL
INDRANIL BISWAS*
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai 400005, India (email: indranil@math.tifr.res.in)
SIDDHARTHA GADGIL
Affiliation:
Department of Mathematics, Indian Institute of Science, Bangalore 560003, India (email: gadgil@math.iisc.ernet.in)
*
✉For correspondence; e-mail: indranil@math.tifr.res.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a geometrically irreducible smooth projective curve defined over ℝ, of genus at least 2, that admits a nontrivial automorphism, σ. Assume that X does not have any real points. Let τ be the antiholomorphic involution of the complexification xℂ of X. We show that if the action of σ on the set 𝒮(X) of all real theta characteristics of X is trivial, then the order of σ is even, say 2k, and the automorphism 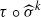of Xℂ has a fixed point, where is the automorphism of X×ℝℂ defined by σ. We then show that there exists X with a real point and admitting a nontrivial automorphism σ, such that the action of σ on 𝒮(X) is trivial, while X/〈σ〉≠ℙ1ℝ. We also give an example of X with no real points and admitting a nontrivial automorphism σ, such that the automorphism 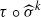has a fixed point, the action of σ on 𝒮(X) is trivial, and X/〈σ〉≠ℙ1ℝ.

Keywords

real curvereal theta characteristicautomorphism

MSC classification

Secondary: 14P25: Topology of real algebraic varieties
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 88 , Issue 1 , February 2010 , pp. 29 - 42
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

References

[1]Arbarello, E., Cornalba, M., Griffiths, P. A. and Harris, J., Geometry of Algebraic Curves, Volume I, Grundlehren der Mathematischen Wissenschaften, 267 (Springer, New York, 1985).CrossRefGoogle Scholar
[2]Atiyah, M. F., ‘Riemann surfaces and spin structures’, Ann. Sci. École Norm. Sup. 4 (1971), 47–62.CrossRefGoogle Scholar
[3]Biswas, I., Gadgil, S. and Sankaran, P., ‘On theta characteristics of a compact Riemann surface’, Bull. Sci. Math. 131 (2007), 493–499.Google Scholar
[4]Gross, B. H. and Harris, J., ‘Real algebraic curves’, Ann. Sci. École. Norm. Sup. 14 (1981), 157–182.CrossRefGoogle Scholar
[5]Kallel, S. and Sjerve, D., ‘Invariant spin structures on Riemann surfaces’, http://arxiv.org/abs/math/0610568.Google Scholar
[6]Mumford, D., ‘Theta characteristics of an algebraic curve’, Ann. Sci. École. Norm. Sup. 4 (1971), 181–192.CrossRefGoogle Scholar
[7]Natanzon, S. M., ‘Spinors and differentials of real algebraic curves’, in: Topology of Real Algebraic Varieties and Related Topics, American Mathematical Society Translations, Series 2, 173 (American Mathematical Society, Providence, RI, 1996), pp. 179–186.Google Scholar