Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cuevas, Claudio
and
Lizama, Carlos
2010.
Semilinear evolution equations on discrete time and maximal regularity.
Journal of Mathematical Analysis and Applications,
Vol. 361,
Issue. 1,
p.
234.
Agarwal, Ravi P.
Cuevas, Claudio
and
Frasson, Miguel V.S.
2012.
Semilinear functional difference equations with infinite delay.
Mathematical and Computer Modelling,
Vol. 55,
Issue. 3-4,
p.
1083.
Agarwal, Ravi P.
Cuevas, Claudio
and
Lizama, Carlos
2014.
Regularity of Difference Equations on Banach Spaces.
p.
19.
Agarwal, Ravi P.
Cuevas, Claudio
and
Lizama, Carlos
2014.
Regularity of Difference Equations on Banach Spaces.
p.
47.
Schwenninger, Felix L.
2016.
Functional calculus estimates for Tadmor–Ritt operators.
Journal of Mathematical Analysis and Applications,
Vol. 439,
Issue. 1,
p.
103.
Badea, Catalin
and
Seifert, David
2016.
Ritt operators and convergence in the method of alternating projections.
Journal of Approximation Theory,
Vol. 205,
Issue. ,
p.
133.
Lizama, Carlos
and
Murillo-Arcila, Marina
2017.
Maximal regularity in l spaces for discrete time fractional shifted equations.
Journal of Differential Equations,
Vol. 263,
Issue. 6,
p.
3175.
Mengestie, Tesfa
2020.
Resolvent growth condition for composition operators on the Fock space.
Annals of Functional Analysis,
Vol. 11,
Issue. 4,
p.
947.
Kumar, Mahesh
2021.
Weighted/unweighted composition operators which are Ritt or unconditional Ritt operators.
Archiv der Mathematik,
Vol. 116,
Issue. 3,
p.
307.
Ri, Myong-Hwan
and
Farwig, Reinhard
2022.
Maximal L1-Regularity of Generators for Bounded Analytic Semigroups in Banach Spaces.
Acta Mathematica Scientia,
Vol. 42,
Issue. 4,
p.
1261.
Mengestie, Tesfa
and
Seyoum, Werkaferahu
2022.
Supercyclicity and Resolvent Condition for Weighted Composition Operators.
Computational Methods and Function Theory,
Vol. 22,
Issue. 1,
p.
157.
Bouabdillah, Oualid
and
Le Merdy, Christian
2024.
Polygonal functional calculus for operators with finite peripheral spectrum.
Israel Journal of Mathematics,
Vol. 263,
Issue. 2,
p.
517.
Bounit, H.
and
Tismane, M.
2024.
On the admissibility and input–output representation for a class of Volterra integro-differential systems.
Mathematics of Control, Signals, and Systems,
Vol. 36,
Issue. 3,
p.
525.
Bounit, H.
Hadd, S.
and
Manar, Y.
2025.
New results on maximal $$L^p$$-regularity of a class of integrodifferential equations.
Archiv der Mathematik,
Vol. 124,
Issue. 3,
p.
325.
Bouabdillah, Oualid
2025.
Square functions associated with RittE operators.
Indagationes Mathematicae,
Schwenninger, Felix L.
and
Wierzba, Alexander A.
2025.
A dual notion to BIBO stability.
Journal of Mathematical Analysis and Applications,
Vol. 545,
Issue. 2,
p.
129156.

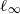 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS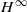 -calculus, and give a complete characterization of this condition in the case of Banach spaces which are
-calculus, and give a complete characterization of this condition in the case of Banach spaces which are 