Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T20:01:24.111Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on converse Carleman and Krein criteria for the classical moment problem

Part of: Distribution theory Distribution theory - Probability Real functions Integral transforms, operational calculus

Published online by Cambridge University Press:  09 April 2009

Anthony G. Pakes
Anthony G. Pakes
Affiliation:
Department of Mathematics and Statistics University of Western Australia35 Stirling Highway, WA 6009Australia e-mail: pakes@maths.uwa.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

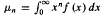The key theme is converse forms of criteria for deciding determinateness in the classical moment problem. A method of proof due to Koosis is streamlined and generalized giving a convexity condition under which moments satisfying 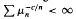implies that 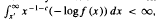c a positive constant. A contrapositive version is proved under a rapid variation condition on f (x), generalizing a result of Lin. These results are used to obtain converses of the Stieltjes versions of the Carleman and Krein criteria. Hamburger versions are obtained which relax the symmetry assumption of Koosis and Lin, respectively. A sufficient condition for Stieltjes determinateness of a discrete law is given in terms of its mass function. These criteria are illustrated through several examples.

Keywords

classical moment problemCarleman and Krein conditionsFenchel transformrapid variation

MSC classification

Secondary: 44A60: Moment problems 62E10: Characterization and structure theory 26A51: Convexity, generalizations 60E05: Distributions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 71 , Issue 1 , August 2001 , pp. 81 - 104
Copyright
Copyright © Australian Mathematical Society 2001

References

[1]Berg, C., ‘Indeterminate moment problems and the theory of entire functions’, J. Comput. Appl. Math. 65 (1995), 27–55.CrossRefGoogle Scholar
[2]Bingham, N. H., Goldie, C. M. and Teugels, J. L., Regular variation (Cambridge Univ. Press, Cambridge, 1987).CrossRefGoogle Scholar
[3]Gabardo, J.-P., ‘A maximum entropy approach to the classical moment problem’, J. Funct. Anal. 106 (1992), 80–94.CrossRefGoogle Scholar
[4]Garnett, J. B., Bounded analytic functions (Academic Press, New York, 1981).Google Scholar
[5]Heyde, C. C., ‘Some remarks on the moment problem, (I) and (II)’, Quart. J. Math. Oxford (2), 14 (1963), 91–105.CrossRefGoogle Scholar
[6]Hiriart-Urruty, J.-B. and Lemaréchal, C., Convex analysis and minimization algorithms I (Springer, Berlin, 1993).CrossRefGoogle Scholar
[7]Koosis, P., The logarithmic integral I (Cambridge Univ. Press, Cambridge, 1988).CrossRefGoogle Scholar
[8]Lin, G. D., ‘On the moment problems’, Statist. Probab. Letters 35 (1997), 85–90.Google Scholar
[9]Pakes, A. G., ‘Length biasing and laws equivalent to the log-normal’, J. Math. Anal. Appl. 197 (1996), 825–854.CrossRefGoogle Scholar
[10]Pakes, A. G., ‘Characterization by invariance under length-biasing and random scaling’, J. Statist. Plann. Inference 63 (1997), 285–310.CrossRefGoogle Scholar
[11]Pakes, A. G., Hung, W.-L. and Wu, J.-W., ‘Criteria for the unique determination of probability distributions by moments’, Aust. N. Z. J. Stat. 43 (2001), 101–111.CrossRefGoogle Scholar
[12]Pedersen, H. L., ‘On Krein's theorem for indeterminacy of the classical moment problem’, J. Approx. Theory 95 (1998), 90–100.CrossRefGoogle Scholar
[13]Samorodnitsky, G. and Taqqu, M. S., Stable non-Gaussian random processes (Chapman and Hall, New York, 1994).Google Scholar
[14]Sjödin, T., ‘A note on the Carleman condition for determinacy of moment problems’, Ark. Mat. 25 (1987), 289–294.CrossRefGoogle Scholar
[15]Slud, E. V., ‘The moment problem for polynomial forms in normal random variables’, Ann. Probab. 21 (1993), 2200–2214.CrossRefGoogle Scholar
[16]Springer, M. D., The algebra of random variables (Wiley, New York, 1979).Google Scholar
[17]Stoyanov, J., Counterexamples in probability, 2nd Edition (Wiley, Chichester, 2000).Google Scholar
[18]Stoyanov, J., ‘Krein condition in probabilistic moment problems’, Bernoulli 6 (2000), 939–949.CrossRefGoogle Scholar
[19]Zolotarev, V. M., One-dimensional stable distributions (American Math. Society, Providence, RI, 1986).CrossRefGoogle Scholar