Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T06:53:02.208Z Has data issue: false hasContentIssue false
  • English
  • Français

RIGIDIFIED TORSOR COCYCLES, HYPERCOVERINGS AND BUNDLE GERBES

Part of: Applied homological algebra and category theory Higher algebraic $K$-theory Homology and cohomology theories Categories and geometry (Co)homology theory

Published online by Cambridge University Press:  07 April 2020

STEFAN SCHRÖER
STEFAN SCHRÖER*
Affiliation:
Mathematisches Institut, Heinrich-Heine-Universität, 40204Düsseldorf, Germany e-mail: schroeer@math.uni-duesseldorf.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a geometric interpretation of sheaf cohomology for higher degrees $n\geq 1$ in terms of torsors on the member of degree 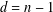$d=n-1$ in hypercoverings of type $r=n-2$, endowed with an additional datum, the so-called rigidification. This generalizes the fact that cohomology in degree one is the group of isomorphism classes of torsors, where the rigidification becomes vacuous, and that cohomology in degree two can be expressed in terms of bundle gerbes, where the rigidification becomes an associativity constraint.

Keywords

cohomologytorsorshypercoveringssimplicial sets

MSC classification

Primary: 55N30: Sheaf cohomology 19D23: Symmetric monoidal categories
Secondary: 55U10: Simplicial sets and complexes 18F20: Presheaves and sheaves 14F20: Étale and other Grothendieck topologies and (co)homologies
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 112 , Issue 1 , February 2022 , pp. 115 - 144
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by M. Murray

References

Artin, M, ‘On the joins of Hensel rings’, Adv. Math. 7 (1971), 282–296.10.1016/S0001-8708(71)80007-5CrossRefGoogle Scholar
Artin, M., Grothendieck, A. and Verdier, J.-L. (eds.), Théorie des topos et cohomologie étale des schémas (SGA 4) Tome 1 (Springer, Berlin, 1972).Google Scholar
Artin, M., Grothendieck, A. and Verdier, J.-L. (eds.), Théorie des topos et cohomologie étale des schémas (SGA 4) Tome 2 (Springer, Berlin, 1973).Google Scholar
Artin, M., Grothendieck, A. and Verdier, J.-L. (eds.), Théorie des topos et cohomologie étale des schémas (SGA 4) Tome 3 (Springer, Berlin, 1973).Google Scholar
Artin, M. and Mazur, B., Etale Homotopy (Springer, Berlin, 1969).CrossRefGoogle Scholar
Beke, T., ‘Higher Čech theory’, K-Theory 32 (2004), 293–322.10.1007/s10977-004-0840-0CrossRefGoogle Scholar
Bertolin, C., ‘Extensions of Picard stacks and their homological interpretation’, J. Algebra 331 (2011), 28–45.CrossRefGoogle Scholar
Bredon, G., Sheaf Theory (McGraw-Hill, New York, 1967).Google Scholar
Breen, L., ‘Differential geometry of gerbes and differential forms’, in: Higher Structures in Geometry and Physics (eds. Cattaneo, A., Giaquinto, A. and Xu, P.) (Birkhäuser, New York, 2011), 57–92.CrossRefGoogle Scholar
Breen, L. and Messing, W., ‘Differential geometry of gerbes’, Adv. Math. 198 (2005), 732–846.10.1016/j.aim.2005.06.014CrossRefGoogle Scholar
Brylinski, J.-L., Loop Spaces, Characteristic Classes and Geometric Quantization (Birkhäuser, Boston, 1993).CrossRefGoogle Scholar
Carey, A., Murray, M. and Wang, B., ‘Higher bundle gerbes and cohomology classes in gauge theories’, J. Geom. Phys. 21 (1997), 183–197.CrossRefGoogle Scholar
Cartan, H. and Eilenberg, S., Homological Algebra (Princeton University Press, Princeton, NJ, 1956).Google Scholar
Dugger, D. and Isaksen, D., ‘Topological hypercovers and 𝔸1 -realizations’, Math. Z. 246 (2004), 667–689.CrossRefGoogle Scholar
Duskin, J., ‘Simplicial methods and the interpretation of “triple” cohomology’, Mem. Amer. Math. Soc. 163 (1975).Google Scholar
Friedlander, E., Étale Homotopy of Simplicial Schemes (Princeton University Press, Princeton, NJ, 1982).Google Scholar
Giraud, J., Cohomologie Non Abélienne (Springer, Berlin, 1971).CrossRefGoogle Scholar
Glenn, P., ‘Realization of cohomology classes in arbitrary exact categories’, J. Pure Appl. Algebra 25 (1982), 33–105.CrossRefGoogle Scholar
Godement, R., Topologie Algébrique et Théorie des Faisceaux (Hermann, Paris, 1964).Google Scholar
Grothendieck, A., ‘A general theory of fibre spaces with structure sheaf’, University of Kansas, Department of Mathematics, Report No. 4.Google Scholar
Grothendieck, A., Revêtements étales et groupe fondamental (SGA 1) (Société Mathématique de France, Paris, 2003).Google Scholar
Hitchin, N., Lectures on Special Lagrangian Submanifolds, Winter School on Mirror Symmetry, Vector Bundles and Lagrangian Submanifolds (eds. Vafa, C. and Yau, S.-T.) (American Mathematical Society, Providence, RI, 1999), 151–182.Google Scholar
Jardine, J., ‘Cocycle categories’, in: Algebraic Topology (eds. Baas, N., Friedlander, E., Jahren, B. and Ostvær, P.) (Springer, Berlin, 2009), 185–218.CrossRefGoogle Scholar
Jardine, J., Local Homotopy Theory (Springer, New York, 2015).CrossRefGoogle Scholar
Kashiwara, M. and Schapira, P., Categories and Sheaves (Springer, Berlin, 2006).CrossRefGoogle Scholar
MacLane, S., ‘Natural associativity and commutativity’, Ric. Univ. Stud. 49 (1963), 28–46.Google Scholar
MacLane, S., Categories for the Working Mathematician (Springer, New York, 1971).Google Scholar
May, J., Simplicial Objects in Algebraic Topology (Van Nostrand, Princeton, NJ, 1967).Google Scholar
Murray, M., ‘Bundle gerbes’, J. Lond. Math. Soc. (2) 54 (1996), 403–416.CrossRefGoogle Scholar
Murray, M., ‘An introduction to bundle gerbes’, in: The Many Facets of Geometry. A Tribute to Nigel Hitchin (eds. García-Prada, O., Bourguignon, J. and Salamon, S.) (Oxford University Press, Oxford, 2010).Google Scholar
Murray, M. and Stevenson, D., ‘Bundle gerbes: stable isomorphism and local theory’, J. Lond. Math. Soc. (2) 62 (2000), 925–937.CrossRefGoogle Scholar
Murray, M. and Stevenson, D., ‘A note on bundle gerbes and infinite-dimensionality’, J. Aust. Math. Soc. 90 (2011), 81–92.CrossRefGoogle Scholar
Schröer, S., ‘Geometry on totally separably closed schemes’, Algebra Number Theory 11 (2017), 537–582.CrossRefGoogle Scholar
Schröer, S., ‘On flasque sheaves and flasque modules’, Appl. Categ. Structures 26 (2018), 1113–1122.CrossRefGoogle Scholar
Schröer, S., ‘Total separable closure and contractions’, J. Algebra 525 (2019), 416–434.CrossRefGoogle Scholar
Segal, G., ‘Classifying spaces and spectral sequences’, Publ. Math. Inst. Hautes Études Sci. 34 (1968), 105–112.CrossRefGoogle Scholar
The Stacks Project Authors: The Stacks Project. http://stacks.math.columbia.edu, 2018.Google Scholar
Weibel, C., An Introduction to Homological Algebra (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar