Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-11T02:46:02.446Z Has data issue: false hasContentIssue false
  • English
  • Français

ROOTS OF DEHN TWISTS ABOUT SEPARATING CURVES

Published online by Cambridge University Press:  17 June 2013

KASHYAP RAJEEVSARATHY
KASHYAP RAJEEVSARATHY*
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research Bhopal, ITI Campus (Gas Rahat) Building, Govindapura, Bhopal 462023, Madhya Pradesh, India email kashyap@iiserb.ac.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 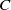$C$ be a curve in a closed orientable surface 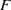$F$ of genus 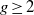$g\geq 2$ that separates 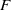$F$ into subsurfaces 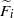$\widetilde {{F}_{i} } $ of genera 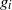${g}_{i} $, for 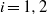$i= 1, 2$. We study the set of roots in 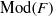$\mathrm{Mod} (F)$ of the Dehn twist 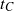${t}_{C} $ about 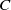$C$. All roots arise from pairs of 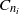${C}_{{n}_{i} } $-actions on the 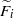$\widetilde {{F}_{i} } $, where 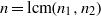$n= \mathrm{lcm} ({n}_{1} , {n}_{2} )$ is the degree of the root, that satisfy a certain compatibility condition. The 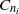${C}_{{n}_{i} } $-actions are of a kind that we call nestled actions, and we classify them using tuples that we call data sets. The compatibility condition can be expressed by a simple formula, allowing a classification of all roots of 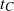${t}_{C} $ by compatible pairs of data sets. We use these data set pairs to classify all roots for 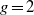$g= 2$ and 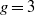$g= 3$. We show that there is always a root of degree at least 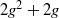$2{g}^{2} + 2g$, while 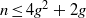$n\leq 4{g}^{2} + 2g$. We also give some additional applications.

Keywords

surfacemapping classDehn twistseparating curveroot
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 2 , October 2013 , pp. 266 - 288
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Conner, P. E. and Raymond, F., ‘Deforming homotopy equivalences to homeomorphisms in aspherical manifolds’, Bull. Amer. Math. Soc. 83 (1) (1977), 36–85.CrossRefGoogle Scholar
Edmonds, A. L., ‘Surface symmetry. I’, Michigan Math. J. 29 (2) (1982), 171–183.CrossRefGoogle Scholar
Harvey, W. J., ‘Cyclic groups of automorphisms of a compact Riemann surface’, Quart. J. Math. Oxford Ser. (2) 17 (1966), 86–97.CrossRefGoogle Scholar
Magnus, W., Karrass, A. and Solitar, D., Combinatorial Group Theory: Presentations of Groups in Terms of Generators and Relations (Dover Publications, Mineola, NY, 2004).Google Scholar
Margalit, D. and Schleimer, S., ‘Dehn twists have roots’, Geom. Topol. 13 (3) (2009), 1495–1497.CrossRefGoogle Scholar
McCullough, D. and Rajeevsarathy, K., ‘Roots of Dehn twists’, Geom. Dedicata 151 (2011), 397–409.CrossRefGoogle Scholar
Nielsen, J., ‘Abbildungsklassen endlicher Ordnung’, Acta Math. 75 (1943), 23–115.CrossRefGoogle Scholar
Rajeevsarathy, K., GAP Software. available at: home.iiserbhopal.ac.in/~kashyap/n2.g.Google Scholar
Scott, P., ‘The geometries of 3-manifolds’, Bull. Lond. Math. Soc. 15 (5) (1983), 401–487.CrossRefGoogle Scholar
Thurston, W. P., The geometry and topology of three-manifolds. notes available at: http://www.msri.org/communications/books/gt3m/PDF.Google Scholar