Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T07:13:45.107Z Has data issue: false hasContentIssue false
  • English
  • Français

ROOTS OF UNITY AS QUOTIENTS OF TWO ROOTS OF A POLYNOMIAL

Part of: Algebraic number theory: global fields Sequences and sets

Published online by Cambridge University Press:  10 August 2012

ARTŪRAS DUBICKAS
ARTŪRAS DUBICKAS*
Affiliation:
Department of Mathematics and Informatics, Vilnius University, Naugarduko 24, Vilnius LT-03225, Lithuania (email: arturas.dubickas@mif.vu.lt)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

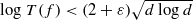Let K be a number field. For f∈K[x], we give an upper bound on the least positive integer T=T(f) such that no quotient of two distinct Tth powers of roots of f is a root of unity. For each ε>0 and each f∈ℚ[x] of degree d≥d(ε) we prove that . In the opposite direction, we show that the constant 2 cannot be replaced by a number smaller than 1 . These estimates are useful in the study of degenerate and nondegenerate linear recurrence sequences over a number field K.

Keywords

root of unitynumber fieldlinear recurrence sequence

MSC classification

Secondary: 11R04: Algebraic numbers; rings of algebraic integers 11B37: Recurrences
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 92 , Issue 2 , April 2012 , pp. 137 - 144
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2012

References

[1]Aschbacher, M. G. and Guralnick, R. M., ‘On Abelian quotients of primitive groups’, Proc. Amer. Math. Soc. 107 (1989), 89–95.CrossRefGoogle Scholar
[2]Berstel, J. and Mignotte, M., ‘Deux propriétés décidables des suites recurrentes linéaires’, Bull. Soc. Math. France 104 (1976), 175–194.CrossRefGoogle Scholar
[3]Drungilas, P. and Dubickas, A., ‘On subfields of a field generated by two conjugate algebraic numbers’, Proc. Edinb. Math. Soc. 47 (2004), 119–123.CrossRefGoogle Scholar
[4]Everest, G., van der Poorten, A., Shparlinski, I. and Ward, T., Recurrence Sequences, Mathematical Surveys and Monographs, 104 (American Mathematical Society, Providence, RI, 2003).CrossRefGoogle Scholar
[5]Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers (Oxford University Press, Oxford, 1979).Google Scholar
[6]Isaacs, I. M., ‘Quotients which are roots of unity (solution of problem 6523)’, Amer. Math. Monthly 95 (1988), 561–562.Google Scholar
[7]Massias, J.-P., ‘Majoration explicite de l’ordre maximum d’un élément du groupe symétrique’, Ann. Fac. Sci. Toulouse Math. 6 (1984), 269–281.CrossRefGoogle Scholar
[8]Massias, J.-P., Nicolas, J.-L. and Robin, G., ‘Evaluation asymptotique de l’ordre maximum d’un élément du groupe symétrique’, Acta Arith. 104 (1988), 221–242.CrossRefGoogle Scholar
[9]Pólya, G., ‘Arithmetische Eigenschaften der Reihenentwicklungen rationaler Funktionen’, J. reine angew. Math. 151 (1921), 1–31.CrossRefGoogle Scholar
[10]Robba, Ph., ‘Zéros de suites récurrentes linéaires’, Groupe Étude Anal. Ultramétrique, 5 (1977/78), Exposé No. 13, 1978, 5 pp.Google Scholar
[11]Schinzel, A., ‘Around Pólya’s theorem on the set of prime divisors of a linear recurrence’, in: Diophantine Equations. Papers from the international conference held in honor of T. N. Shorey’s 60th birthday, Mumbai, 16–20 December 2005, (ed. Saradha, N.) (Narosa Publishing House, New Delhi, 2008), pp. 225–233.Google Scholar
[12]Shah, S., ‘An inequality for the arithmetical function g(x)’, J. Indian Math. Soc. 3 (1939), 316–318.Google Scholar
[13]Szalay, M., ‘On the maximal order in S n and S *n’, Acta Arith. 37 (1980), 321–331.CrossRefGoogle Scholar
[14]Yokoyama, K., Li, Z. and Nemes, I., ‘Finding roots of unity among quotients of the roots of an integral polynomial’, in: Proceedings of the 1995 International Symposium on Symbolic and Algebraic Computation, ISSAC’95, Montreal, 10–12 July 1995, (ed. Levelt, A. H. M.) (ACM Press, New York, 1995), pp. 85–89.Google Scholar