Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T19:50:12.032Z Has data issue: false hasContentIssue false
  • English
  • Français

The second dual of C0 (S, A)

Part of: Commutative Banach algebras and commutative topological algebras Measures, integration, derivative, holomorphy

Published online by Cambridge University Press:  09 April 2009

Stephen T. L. Choy  and
James C. S. Wong
Stephen T. L. Choy
Affiliation:
National University of Singapore, Republic of Singapore
James C. S. Wong
Affiliation:
The University of Calgary, Canada, T2N 1N4
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The second dual of the vector-valued function space C0(S, A) is characterized in terms of generalized functions in the case where A* and A** have the Radon-Nikodým property. As an application we present a simple proof that C0 (S, A) is Arens regular if and only if A is Arens regular in this case. A representation theorem of the measure μh is given, where 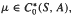, h ∈ L∞ (|μ;|, A**) and μh is defined by the Arens product.

MSC classification

Secondary: 46G10: Vector-valued measures and integration 46J10: Banach algebras of continuous functions, function algebras
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 56 , Issue 3 , June 1994 , pp. 303 - 313
Copyright
Copyright © Australian Mathematical Society 1994

References

[1]Batt, J. and Berg, E. J., ‘Linear bounded transformations on the space of continuous functions’, J. Funct. Anal. 4 (1969), 215–239.CrossRefGoogle Scholar
[2]Brooks, J. K. and Lewis, P. W., ‘Linear operators and vector measures’, Trans. Amer. Math. Soc. 192 (1974), 139–162.CrossRefGoogle Scholar
[3]Cambern, M. and Grein, P., ‘The bidual of C(X, E)’, Proc. Amer. Math. Soc. 85 (1982), 53–58.Google Scholar
[4]Choy, S. T. L., ‘Extreme operators on function spaces’, Illinois J. Math. 33 (1989), 301–309.CrossRefGoogle Scholar
[5]Choy, S. T. L., ‘Positive operators and algebras of dominated measures’, Rev. Roumaine Math. Pures Appl. 34 (1989), 213–219.Google Scholar
[6]Diestal, J. and Uhl, J. J., Vector measures, Math. Surveys 15 (Amer. Math. Soc., Providence, R.I., 1977).CrossRefGoogle Scholar
[7]Diestel, J., Sequences and series in Banach spaces, Graduate Texts in Math. 92 (Springer, New York, 1984).CrossRefGoogle Scholar
[8]Dinculeanu, N., Vector measures (Pergamon Press, New York, 1967).CrossRefGoogle Scholar
[9]Duncan, J. and Hosseinium, S. A. R., ‘The second dual of a Banach algebra’, Proc. Roy. Soc. Edinburgh Sect. A 84 (1979), 309–325.CrossRefGoogle Scholar
[10]Husain, T., ‘Amenability of locally compact groups and vector-valued function spaces’, Sympos. Math. 16 (1975), 417–431.Google Scholar
[11]Ülger, A., ‘Arens regularity of the algebra C(K, A)’, to appear.Google Scholar
[12]Wong, J. C., ‘Abstract harmonic analysis of generalized functions on locally compact semi-groups with applications to invariant means’, J. Austral. Math. Soc. (Series A) 23 (1977), 84–94.CrossRefGoogle Scholar