Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sarfraz, Naqash
and
Hussain, Amjad
2019.
Estimates for the Commutators of p-Adic Hausdorff Operator on Herz-Morrey Spaces.
Mathematics,
Vol. 7,
Issue. 2,
p.
127.
Hussain, Amjad
and
Sarfraz, Naqash
2019.
The Hausdorff Operator on Weighted p-Adic Morrey and Herz Type Spaces.
p-Adic Numbers, Ultrametric Analysis and Applications,
Vol. 11,
Issue. 2,
p.
151.
Wei, Mingquan
2021.
Estimates for the Product Weighted Hardy–Littlewood Average and Its Commutator on Product Central Morrey Spaces.
Mediterranean Journal of Mathematics,
Vol. 18,
Issue. 6,
Wei, Mingquan
2022.
A characterization of CMO˙q→ via the commutator of Hardy-type operators on mixed Herz spaces.
Applicable Analysis,
Vol. 101,
Issue. 16,
p.
5727.
Wei, Mingquan
He, Qianjun
Li, Xiang
Wang, Zequn
and
Sawano, Yoshihiro
2022.
Sharp Constants for
q
-Analogue of Hausdorff Operators on Central
q
-Morrey Spaces.
Journal of Function Spaces,
Vol. 2022,
Issue. ,
p.
1.
An, Na
Wei, Mingquan
and
Zhao, Fayou
2023.
Sharp constants for multilinear Hausdorff operators on local Morrey-type spaces.
Forum Mathematicum,
Vol. 35,
Issue. 4,
p.
1133.
Wei, Mingquan
and
Liu, Xiaoyu
2023.
Sharp weak bounds for discrete Hardy operator on discrete central Morrey spaces.
AIMS Mathematics,
Vol. 8,
Issue. 2,
p.
5007.
Liu, Xiaoyu
Wei, Mingquan
Song, Pengchao
and
Yan, Dunyan
2024.
Sharp reverse fractional Hausdorff inequality on power-weighted Lebesgue spaces.
Journal of Pseudo-Differential Operators and Applications,
Vol. 15,
Issue. 3,
Sarfraz, Naqash
Riaz, Muhammad Bilal
Mehmood, Sajid
Zaman, Mir
and
Khan, Abdul Rauf
2024.
Characterization of p‐Adic Mixed λ‐Central Bounded Mean Oscillation Space via Commutators of p‐Adic Hardy‐Type Operators.
Journal of Function Spaces,
Vol. 2024,
Issue. 1,
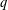 $q$-INEQUALITIES
$q$-INEQUALITIES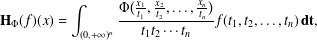 $$\begin{eqnarray}\mathbf{H}_{\unicode[STIX]{x1D6F7}}(f)(x)=\int _{(0,+\infty )^{n}}{\displaystyle \frac{\unicode[STIX]{x1D6F7}\big(\frac{x_{1}}{t_{1}},\frac{x_{2}}{t_{2}},\ldots ,\frac{x_{n}}{t_{n}}\big)}{t_{1}t_{2}\cdots t_{n}}}f(t_{1},t_{2},\ldots ,t_{n})\,\mathbf{dt},\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{H}_{\unicode[STIX]{x1D6F7}}(f)(x)=\int _{(0,+\infty )^{n}}{\displaystyle \frac{\unicode[STIX]{x1D6F7}\big(\frac{x_{1}}{t_{1}},\frac{x_{2}}{t_{2}},\ldots ,\frac{x_{n}}{t_{n}}\big)}{t_{1}t_{2}\cdots t_{n}}}f(t_{1},t_{2},\ldots ,t_{n})\,\mathbf{dt},\end{eqnarray}$$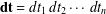 $\mathbf{dt}=dt_{1}\,dt_{2}\cdots \,dt_{n}$ or
$\mathbf{dt}=dt_{1}\,dt_{2}\cdots \,dt_{n}$ or 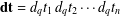 $\mathbf{dt}=d_{q}t_{1}\,d_{q}t_{2}\cdots d_{q}t_{n}$ is the discrete measure in
$\mathbf{dt}=d_{q}t_{1}\,d_{q}t_{2}\cdots d_{q}t_{n}$ is the discrete measure in 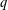 $q$-analysis. The sharp bounds for the multivariate Hausdorff operator on spaces
$q$-analysis. The sharp bounds for the multivariate Hausdorff operator on spaces 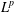 $L^{p}$ with power weights are calculated, where
$L^{p}$ with power weights are calculated, where  $p\in \mathbb{R}\backslash \{0\}$.
$p\in \mathbb{R}\backslash \{0\}$.