Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T20:11:26.416Z Has data issue: false hasContentIssue false
  • English
  • Français

SHORT INTERVALS ASYMPTOTIC FORMULAE FOR BINARY PROBLEMS WITH PRIME POWERS, II

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  08 April 2019

ALESSANDRO LANGUASCO Open the ORCID record for ALESSANDRO LANGUASCO [Opens in a new window]  and
ALESSANDRO ZACCAGNINI Open the ORCID record for ALESSANDRO ZACCAGNINI [Opens in a new window]
ALESSANDRO LANGUASCO*
Affiliation:
Università di Padova, Dipartimento di Matematica ‘Tullio Levi-Civita’, Via Trieste 63, 35121Padova, Italy
ALESSANDRO ZACCAGNINI
Affiliation:
Università di Parma, Dipartimento di Scienze Matematiche, Fisiche e Informatiche, Parco Area delle Scienze 53/a, 43124Parma, Italy e-mail: alessandro.zaccagnini@unipr.it
*
e-mail: alessandro.languasco@unipd.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We improve some results in our paper [A. Languasco and A. Zaccagnini, ‘Short intervals asymptotic formulae for binary problems with prime powers’, J. Théor. Nombres Bordeaux30 (2018) 609–635] about the asymptotic formulae in short intervals for the average number of representations of integers of the forms 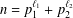$n=p_{1}^{\ell _{1}}+p_{2}^{\ell _{2}}$ and 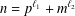$n=p^{\ell _{1}}+m^{\ell _{2}}$, where 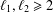$\ell _{1},\ell _{2}\geq 2$ are fixed integers, 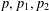$p,p_{1},p_{2}$ are prime numbers and $m$ is an integer. We also remark that the techniques here used let us prove that a suitable asymptotic formula for the average number of representations of integers 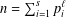$n=\sum _{i=1}^{s}p_{i}^{\ell }$, where $s$, 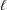$\ell$ are two integers such that 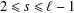$2\leq s\leq \ell -1$, 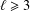$\ell \geq 3$ and 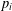$p_{i}$, 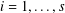$i=1,\ldots ,s$, are prime numbers, holds in short intervals.

Keywords

Waring–Goldbach problemHardy–Littlewood method

MSC classification

Primary: 11P32: Goldbach-type theorems; other additive questions involving primes
Secondary: 11P55: Applications of the Hardy-Littlewood method 11P05: Waring's problem and variants
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 3 , December 2020 , pp. 351 - 370
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by I. Shparlinski

References

Cantarini, M., Gambini, A. and Zaccagnini, A., ‘On the average number of representations of an integer as a sum of like powers’, 2018, https://arxiv.org/pdf/1805.09008.pdf.Google Scholar
Gambini, A., Languasco, A. and Zaccagnini, A., ‘A Diophantine approximation problem with two primes and one k-power of a prime’, J. Number Theory 188 (2018), 210–228.Google Scholar
Kumchev, A. and Tolev, D., ‘An invitation to additive prime number theory’, Serdica Math. J. 31 (2005), 1–74.Google Scholar
Languasco, A. and Zaccagnini, A., ‘On a ternary Diophantine problem with mixed powers of primes’, Acta Arith. 159 (2013), 345–362.Google Scholar
Languasco, A. and Zaccagnini, A., ‘Short intervals asymptotic formulae for binary problems with primes and powers, II: density 1’, Monatsh. Math. 181 (2016), 419–435.Google Scholar
Languasco, A. and Zaccagnini, A., ‘Sum of one prime and two squares of primes in short intervals’, J. Number Theory 159 (2016), 45–58.Google Scholar
Languasco, A. and Zaccagnini, A., ‘Short intervals asymptotic formulae for binary problems with primes and powers, I: density 3/2’, Ramanujan J. 42 (2017), 371–383.Google Scholar
Languasco, A. and Zaccagnini, A., ‘Short intervals asymptotic formulae for binary problems with prime powers’, J. Théor. Nombres Bordeaux 30 (2018), 609–635.Google Scholar
Languasco, A. and Zaccagnini, A., ‘Sum of four prime cubes in short intervals’, Acta Math. Hungar. (2019), to appear.Google Scholar
Montgomery, H. L., Ten Lectures on the Interface Between Analytic Number Theory and Harmonic Analysis, CBMS Regional Conference Series in Mathematics, 84 (American Mathematical Society, Providence, RI, 1994).Google Scholar
Suzuki, Y., ‘A note on the sum of a prime and a prime square’, in: Analytic and Probabilistic Methods in Number Theory, Proc. Sixth Int. Conf., Palanga, Lithuania, 11–17 September 2016 (Vilnius University Publishing House, Vilnius, 2017), 221–226.Google Scholar
Suzuki, Y., ‘On the sum of a prime number and a square number’, Preprint, 2017, http://www.math.sci.hokudai.ac.jp/∼wakate/mcyr/2017/pdf/01500_suzuki_yuta.pdf.Google Scholar
Tolev, D., ‘On a Diophantine inequality involving prime numbers’, Acta Arith. 61 (1992), 289–306.Google Scholar
Vaughan, R. C., The Hardy–Littlewood Method, 2nd edn (Cambridge University Press, Cambridge, 1997).Google Scholar
Vaughan, R. C. and Wooley, T. D., ‘Waring’s problem: a survey’, in: Number Theory for the Millennium, Vol. III (A. K. Peters, Natick, MA, 2002), 301–340.Google Scholar