SMALL-SCALE EQUIDISTRIBUTION OF RANDOM WAVES GENERATED BY AN UNFAIR COIN FLIP

Abstract

In this paper we study the small-scale equidistribution property of random waves whose coefficients are determined by an unfair coin. That is, the coefficients take value 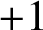$+1$ with probability p and 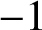$-1$ with probability 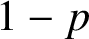$1-p$ . Random waves whose coefficients are associated with a fair coin are known to equidistribute down to the wavelength scale. We obtain explicit requirements on the deviation from the fair ( 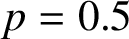$p=0.5$ ) coin to retain equidistribution.

1 Introduction

Lately there has been a renewed interest in the properties of random waves, in particular their small-scale equidistribution properties. Berry [1] introduced ensembles of random waves as a model for chaotic billiards. Random waves are functions of $\mathbb {R}^{n}$ of the form

(1-1) $$ \begin{align}\sum_{\xi_{j}\in \Lambda}C_{j}e^{i\lambda x\cdot\xi_{j}}\end{align} $$

where the coefficients $C_{j}$ are chosen according to some probability distribution and $\Lambda \subset \mathbb {S}^{n-1}$ . Common choices of coefficients include independent random variables such as Gaussian or Rademacher random variables (see, for instance, [1, 3, 11]) and uniform probability densities on high-dimensional unit spheres (see, for instance, [2, 4, 6, 10, 12]). Usually $\Lambda $ is chosen so that the directions $\xi _{j}$ are equally spaced with spacing less than one wavelength, $\lambda ^{-1}$ .

The property of equidistribution (in configuration space) is that the $L^{2}$ density of u is equally spread throughout the domain. Since random waves are defined on an infinite domain, typically studies on random waves restrict attention to the ball of radius one about zero and normalise so that

$$ \begin{align*}\mathbb{E}\bigg[\int_{B_{1}(0)}\vert u(x)\vert^{2}\,dx\bigg]=\mathrm{Vol}(B_{1}(0)).\end{align*} $$

In the sense of Berry’s model we should understand random waves as representing the behaviour of quantum states in chaotic systems. Therefore, by restricting to the ball of radius one about zero we are defining this space to act as our ‘universe’ and the normalisation convention tells us that (at least in expectation) the state lives in the universe with probability one. In the context of this normalisation we say that a random wave is strongly equidistributed on a set $X\subset B_{1}(0)$ if

(1-2) $$ \begin{align} \mathbb{E}\bigg[\int_{X}\vert u(x)\vert^{2}\,dx\bigg]=\mathrm{Vol}(X)(1+o(1))\end{align} $$

and

(1-3) $$ \begin{align} \sigma^{2}\bigg[\int_{X}\vert u(x)\vert^{2}\,dx\bigg]=o((\mathrm{Vol}(X))^{2}).\end{align} $$

In this paper we also allow for a concept of weak equidistribution where (1-3) holds but (1-2) is replaced by

(1-4) $$ \begin{align} c\mathrm{Vol}(X)\leq \mathbb{E}\bigg[\int_{X}\vert u(x)\vert^{2}\,dx\bigg]\leq C\mathrm{Vol}(X).\end{align} $$

So, in the setting of weak equidistribution, the probability of a state being located in the set X is proportional to the volume of X.

In this paper we are interested in the two-dimensional problem where X is a small ball (one whose radius decays to zero as some power of $\lambda ^{-1}$ ). For convenience we consider the ball about the origin; however, none of our analysis is dependent on this centre point, so the results hold for balls centred around general points ${p\in \mathbb {R}^{2}}$ . In the setting of manifolds the question of equidistribution on small balls where the coefficients are uniformly distributed on the sphere or Gaussian are resolved in [5] and [3], respectively. While Rademacher coefficients have not been explicitly studied, most of the results of [3] rely on properties of Gaussian random variables that are shared by Rademacher coefficients. The conclusion of these papers is that strong equidistribution of random waves holds on small balls of radius $\lambda ^{-\alpha }$ so long as $\alpha <1$ . Here we consider a variant of the Rademacher $\pm 1$ coefficients, one associated with an ‘unfair coin’. That is, we assign each coefficient the value $+1$ with probability p and $-1$ with probability $1-p$ . As with Rademacher and Gaussian coefficients, the individual coefficients remain independent of each other. We ask just how unfair the coin has to be before we lose the property of equidistribution.

Before stating the theorems of this paper it is worth considering how large $\int _{B_{r}(0)}\vert u(x)\vert ^{2}\,dx$ can be if we do not randomise coefficients. From Sogge [8], we see that for eigenfunctions (and in fact spectral clusters) on Riemannian manifolds $(M,g)$ ,

(1-5) $$ \begin{align}|\!|{u}|\!|_{L^{2}(B_{r}(0))}\leq r^{1/2}|\!|{u}|\!|_{L^{2}(M)}\end{align} $$

and that in fact this upper bound has sharp examples. The same is true for approximate eigenfunctions on $\mathbb {R}^{2}$ . Consider, for example, the function given by

$$ \begin{align*}v(x)=\lambda^{1/2}\int_{\mathbb{S}}e^{i\lambda x\cdot \xi}\,d\mu(\mathbb{S}),\end{align*} $$

that is, the ( $L^{2}$ normalised) inverse Fourier transform of the surface measure of the unit circle $\mathbb {S}$ . This example has a significant history in the analysis of restriction operators and is the standard example for sharpness of the Fourier restriction problem when $p<2n/(n+1)$ (see, for example, [9, Section 1.2]). Using the method of stationary phase, it can be shown that

$$ \begin{align*}\vert v(x)\vert=C(1+\lambda\vert x\vert)^{-{1}/{2}}\end{align*} $$

and therefore $v(x)$ saturates (1-5). For comparison an equidistributed eigenfunction would have $|\!|{u}|\!|_{L^{2}(B_{r}(0))}\approx r|\!|{u}|\!|_{L^{2}(M)}$ .

Let us look at the extreme case of a completely unfair coin. In this case we always have a coefficient of $+1$ . Then

(1-6) $$ \begin{align}u=\sum_{\xi_{j}\in \Lambda}e^{i\lambda x\cdot \xi_{j}}.\end{align} $$

Supposing that the $\xi _{j}$ are spaced at scales much smaller than the wavelength, we would then expect to be able to replace the sum in (1-6) with an integral (and indeed in Section 3 we perform just such a replacement). Then

$$ \begin{align*}u=C_{\Lambda}\int e^{i\lambda x\cdot \xi}\,d\mu(\mathbb{S})+\text{Error},\end{align*} $$

where $C_{\Lambda }$ is a renormalisation constant that depends on the number of elements of $\Lambda $ and the error term is small enough to be ignored. Notice that in this case u is (up to a constant and an error term) equal to the inverse Fourier transform of surface measure. Therefore, in the extreme case of a completely unfair coin the growth of random waves on small balls is no better than that of eigenfunctions in general, while those associated with a completely fair coin are equidistributed.

We now address the intermediate cases. For the purposes of this paper, rather than considering

$$ \begin{align*}\int_{B_{0}(r)}\vert u(x)\vert^{2}\,dx\end{align*} $$

for $r=\lambda ^{-\alpha }$ , we look at a smoothed version,

$$ \begin{align*}\int a^{2}(\lambda^{\alpha}\vert x\vert)\vert u(x)\vert^{2}\,dx,\end{align*} $$

where $a(r)$ is a smooth, cut-off function supported on $[-2,2]$ and assumed to be equal to one on $[-1,1]$ . We first obtain upper bounds for

$$ \begin{align*}\mathbb{E}[|\!|{a_{\lambda}u}|\!|_{L^{2}}^{2}]=\mathbb{E}\bigg[\int a_{\lambda}(x)\vert u(x)\vert^{2}\,dx\bigg]=\mathbb{E}\bigg[\int a^{2}(\lambda^{\alpha}\vert x\vert)\vert u(x)\vert^{2}\,dx\bigg]\end{align*} $$

in the case where $\Lambda $ is a set of $N=\gamma \lambda $ equispaced directions $\xi _{j}$ with $(\lambda \gamma )^{-1}$ spacing.

Theorem 1.1. Suppose u is a random wave given by (1-1) where $\Lambda $ is a set of equispaced directions $\xi _{j}$ with spacing $(\lambda \gamma )^{-1}$ , and the coefficients are independent random variables each taking the value $+1$ with probability p and $-1$ with probability $1-p$ . Then, for $\alpha <1$ ,

$$ \begin{align*}\mathbb{E}[|\!|{a_{\lambda}u}|\!|_{L^{2}}^{2}]\leq C(\gamma\lambda^{1-2\alpha}+(2p-1)^{2}\gamma^{2}\lambda^{1-\alpha}).\end{align*} $$

Ideally we would also like to obtain a lower bound (since this would allow us to explore weak equidistribution). To obtain the lower bound it is necessary to replace various sums with integrals; see Section 3. This replacement should be understood as giving us lower bounds when the spacing between directions becomes significantly smaller than the wavelength associated with the oscillation. In our model this would correspond to making $\gamma $ large.

Theorem 1.2. Suppose u is a random wave given by (1-1) where $\Lambda $ is a set of equispaced directions $\xi _{j}$ with spacing $(\lambda \gamma )^{-1}$ , and the coefficients are independent random variables each taking the value $+1$ with probability p and $-1$ with probability $1-p$ . Then, for $\alpha <1$ ,

$$ \begin{align*} c(\gamma\lambda^{1-2\alpha}+(2p-1)^{2}\gamma^{2}\lambda^{1-\alpha})\leq \mathbb{E}[|\!|{a_{\lambda}u}|\!|_{L^{2}}^{2}]\leq C(\gamma\lambda^{1-2\alpha}+(2p-1)^{2}\gamma^{2}\lambda^{1-\alpha}).\end{align*} $$

The final ingredient in our understanding of equidistribution is control of the variance. Note that the expectation could be equidistributed by the values fluctuating wildly so that a ‘typical’ random wave was in fact not equidistributed. This is indeed the case for the ‘fair coin’ distribution on balls smaller than the wavelength, $r\leq \lambda ^{-1}$ . If, however, the variance decays in comparison to the (normalised) volume of the ball, then typical random waves from this distribution will equidistribute.

Theorem 1.3. Suppose u is a random wave given by (1-1), where $\Lambda $ is a set of equispaced directions $\xi _{j}$ with spacing $(\lambda \gamma )^{-1}$ , and the coefficients are independent random variables each taking the value $+1$ with probability p and $-1$ with probability $1-p$ . Then, for $\alpha <1$ ,

$$ \begin{align*} \sigma^{2}[|\!|{a_{\lambda}u}|\!|_{L^{2}}^{2}]&\leq C_1\lambda^{1-3\alpha}\gamma^{2}(1-(2p-1)^{2})^2\\&\quad+C_2\gamma^3\lambda^{1-2\alpha}(2p-1)^2(1-(2p-1)^2).\end{align*} $$

Now we can begin to answer the question of equidistribution. We will normalise so that $\mathbb {E}(|\!|{a_{1}u}|\!|_{L^{2}})=1$ for a fair coin randomisation and compare our results to their normalised volume. As we will see from the expectation calculation in Section 2, this normalisation can be achieved by multiplying u by a prefactor of $\gamma ^{-1/2}\lambda ^{-1/2}$ . Recall that we are assuming $\gamma $ is large; we do not, however, want to take it too large (doing so reduces orthogonality relationships). Our interest is in balls so that $1/r$ grows as a power of $\lambda $ . To that end we choose a softer growth rate for $\gamma $ and, while we allow $\gamma \to \infty $ , we assume that $\gamma \leq \log (\lambda )$ .

From Corollary 3.4 we see that equidistribution is preserved if

$$ \begin{align*} p=0.5+\mathcal{O}( \lambda^{-\alpha/2}\gamma^{-{1}/{2}}), \end{align*} $$

so if we also assume only a logarithmic type growth for $\gamma $ , any probability of the form $p=0.5+\lambda ^{-\beta }$ , where $\beta>\alpha /2$ , retains the correct expectation. Using Theorem 1.3 (and normalising), we get that a normalised unfair random wave has variance bounded by

$$ \begin{align*}C_1\lambda^{-1-3\alpha}(1-(2p-1)^2)^{2}+C_2\gamma\lambda^{-1-2\alpha}(2p-1)^2(1-(2p-1)^2).\end{align*} $$

Using the condition for equidistribution from Corollary 3.4, the second term is of the same size as the first term:

$$ \begin{align*}\sigma^2\leq C_1\lambda^{-1-3\alpha}(1-(2p-1)^2)^{2}+C_2\lambda^{-1-3\alpha}(1-(2p-1)^2).\end{align*} $$

So, as long as $\alpha <1$ , the variance is sufficiently controlled for p sufficiently close to 0.5. This is discussed in further detail in the lead-up to Corollary 4.2.

This paper is arranged in the following fashion. First, in Section 2, we obtain the upper bound of Theorem 1.1. Then, in Section 3, we replace the sums appearing in our expression for the expectation with integrals. We are then able to compute those integrals via the method of stationary phase to obtain Theorem 1.2. Finally, in Section 4, we obtain the upper bounds on the variance given in Theorem 1.3.

In this paper we adopt the notation $f\lesssim g$ to mean that

$$ \begin{align*}f\leq Cg, \end{align*} $$

where C is a constant independent of the parameters $\lambda $ and $\gamma $ but which may change from line to line.

2 Proof of Theorem 1.1

In this section we will obtain an upper bound on $\mathbb {E}(|\!|{a_{\lambda }u}|\!|_{L^{2}}^{2})$ for any set of directions $\Lambda $ that are equally spaced on $\mathbb {S}$ . Later we will use this and an approximation of sums by integrals to obtain more refined asymptotics. First, we write

$$ \begin{align*}\mathbb{E}(\lVert a_\lambda u\rVert^2)=\sum_{k}P_k\int{\sum_{j,l}C^{(k)}_jC^{(k)}_la^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot\xi_j}e^{-i\lambda x\cdot\xi_l}\,dx}, \end{align*} $$

where $P_k$ is the probability of a random C-vector (the vector that stores the values of the $C_j$ ) being $C^{(k)}$ and sums over k represent the sum over all C-vectors. The sum $\sum _kP_k$ is equal to 1.

Since there are only a finite number of j and l (N of each), there are $N^2$ pairs and there are a finite number $(2^N)$ of possible C-vectors. This means that both sums involved in the expectation value are finite, so they converge, and their order can be interchanged. Similarly, finite sums commute with integrals so their order can also be swapped, giving

(2-1) $$ \begin{align} \mathbb{E}(\lVert a_\lambda u\rVert^2)&=\sum_{j,l}\bigg(\sum_kP_kC^{(k)}_jC^{(k)}_l\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg)\notag\\&=\sum_{j}\bigg(\sum_{k}P_k(C^{(k)}_j)^2\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(0)}\,dx}\bigg)\notag\\&\quad+\sum_{\substack{j,l\\j\neq l}}\bigg(\sum_kP_kC^{(k)}_jC^{(k)}_l\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg)\notag\\&=\sum_j\sum_kP_k\int{a^{2}(\lambda^\alpha \vert x\vert)\,dx}\notag\\&\quad+\sum_{\substack{j,l\\j\neq l}}\bigg(\sum_kP_kC^{(k)}_jC^{(k)}_l\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg)\notag\\&=N\int{a^{2}(\lambda^\alpha \vert x\vert)\,dx}\notag\\&\quad+\sum_{\substack{j,l\\j\neq l}}\bigg(\sum_kP_kC^{(k)}_jC^{(k)}_l\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg)\notag\\&=N|\!|{a^{2}_{\lambda}}|\!|_{L^{1}}+\sum_{\substack{j,l\\j\neq l}}\bigg(\sum_kP_kC^{(k)}_jC^{(k)}_l\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg). \end{align} $$

From here on, we will refer to the first term in expression (2-1) as the diagonal term and to the second as the off-diagonal terms. To progress in the calculation we need to evaluate $\sum _kP_kC_j^{(k)}C_l^{(k)}$ in terms of p.

Lemma 2.1. For each $j\neq l$ pair, where the coefficients $C_j$ and $C_l$ are independent random variables that take on the value $+1$ with a probability of p or $-1$ with a probability of $1-p$ ,

$$ \begin{align*}\sum_kP_kC^{(k)}_jC^{(k)}_l=(2p-1)^2.\end{align*} $$

Proof. Since $\sum _kP_kC_j^{(k)}C_l^{(k)}=\mathbb {E}(C_j^{(k)}C_l^{(k)})$ and the values of entries j and l are independent of each other, $\mathbb {E}(C_j^{(k)}C_l^{(k)})=\mathbb {E}(C_j^{(k)})\cdot \mathbb {E}(C_l^{(k)})$ . As the probability of $C_j^{(k)}$ being $+1$ is p and the probability of $C_j^{(k)}$ being $-1$ is $1-p$ ,

$$ \begin{align*}\mathbb{E}(C_j^{(k)})=\sum_kP_kC_j^{(k)}=(+1)p+(-1)(1-p)=2p-1.\end{align*} $$

Therefore,

$$ \begin{align*}\sum_kP_kC_j^{(k)}C_l^{(k)}=\mathbb{E}(C_j^{(k)}C_l^{(k)})=(2p-1)^2.\end{align*} $$

This concludes the proof.

Now that we have evaluated $\sum _kP_kC_j^{(k)}C_l^{(k)}$ in terms of p, we can substitute this into (2-1) to give

(2-2) $$ \begin{align} \mathbb{E}(\lVert a_\lambda u\rVert^2)&=N|\!|{a^{2}_{\lambda}}|\!|_{L^{1}}+(2p-1)^2\sum_{\substack{j,l\\j\neq l}}\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\\ &=\gamma\lambda|\!|{a^{2}_{\lambda}}|\!|_{L^{1}}+(2p-1)^2\sum_{\substack{j,l\\j\neq l}}\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}.\notag \end{align} $$

Note that since $a_{\lambda }$ is supported on the ball of radius $2\lambda ^{-\alpha }$ we can say that $|\!|{a^{2}_{\lambda }}|\!|_{L^{1}}\leq C\lambda ^{-2\alpha }$ and arrive at

(2-3) $$ \begin{align} \mathbb{E}(\lVert a_\lambda u\rVert^2)\leq C\gamma\lambda^{1-2\alpha}+(2p-1)^2\sum_{\substack{j,l\\j\neq l}}\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx.}\end{align} $$

Therefore, all that remains in order to obtain the upper bound is to estimate the integrals in the off-diagonal terms. These are oscillatory integrals. Oscillatory integrals are integrals that involve a highly oscillatory function, which alternates between positive and negative values, so that there is a high degree of cancellation. The frequency at which the function is oscillating determines how much cancellation there is, and for high frequencies we can often use the oscillation to get a decay in the size of the integral. For the specific integral in our expression (2-3), we address this in the following theorem.

Theorem 2.2. If $a(\lambda ^\alpha \vert x\vert )$ is a smooth cut-off function with compact support on the ball of radius $r=2\lambda ^{-\alpha }$ centred at 0, and $\xi _j-\xi _l\neq 0$ , then for all $n\in \mathbb {N}$ ,

$$ \begin{align*}\bigg\lvert\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg\rvert\leq C_n\lambda^{-2\alpha}\bigg(\frac{\lambda^{\,(-1+\alpha)}}{\vert\,\xi_j-\xi_l\vert}\bigg)^n.\end{align*} $$

Proof. In these oscillatory integrals $\phi (x)=x\cdot (\xi _j-\xi _l)$ . Due the properties of the exponential function we can write

$$ \begin{align*}\int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}=\int{\frac{1}{i\lambda\partial_v\phi(x)}a^{2}(\lambda^\alpha \vert x\vert) \partial_v(e^{i\lambda x\cdot(\xi_j-\xi_l)})\,dx},\end{align*} $$

where v is a normalised direction vector and $\partial _v$ is the directional derivative in the direction of v. Since $\nabla \phi (x)=\xi _j-\xi _l$ is constant and nonzero, it makes sense to pick $v={\nabla \phi (x)}/{\vert \nabla \phi (x)\vert }$ since this will give the most effective upper bound as the directional derivative will take its maximum value of $\vert \nabla \phi (x)\vert =\vert \xi _j-\xi _l\vert $ . Therefore, we can use integration by parts in the direction of the gradient to transfer the derivative from the exponential to $a_\lambda $ :

(2-4) $$ \begin{align} \int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}=\int{\frac{-1}{i\lambda\vert\xi_j-\xi_l\vert}e^{i\lambda x\cdot(\xi_j-\xi_l)}\lambda^\alpha\partial_v(a^{2}(\lambda^\alpha \vert x\vert))\,dx}. \end{align} $$

The boundary terms are zero due to the cut-off function $a^{2}(\lambda ^\alpha x)$ . Equation (2-4) is the base case for the inductive argument we use to show that, for all $n\in \mathbb {N}$ ,

(2-5) $$ \begin{align} \int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}=\int{\bigg(\frac{-1}{i\lambda\vert\xi_j-\xi_l\vert}\bigg)^ne^{i\lambda x\cdot(\xi_j-\xi_l)}\lambda^{n\alpha}\partial_v^{(n)}(a^{2}(\lambda^\alpha \vert x\vert))\,dx}. \end{align} $$

To complete the inductive argument we must show that if it is true for k, it is true for $k+1$ :

$$ \begin{align*} \int{a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}&=\int{\bigg(\frac{-1}{i\lambda\vert\xi_j-\xi_l\vert}\bigg)^k\frac{1}{i\lambda\vert\xi_j-\xi_l\vert}\lambda^{k\alpha}\partial_v^{(k)}(a^{2}(\lambda^\alpha \vert x\vert))\cdot\partial_v(e^{i\lambda x\cdot(\xi_j-\xi_l)})\,dx}\notag\\ &=\int-\bigg(\frac{-1}{i\lambda\vert\xi_j-\xi_l\vert}\bigg)^k\frac{1}{i\lambda\vert\xi_j-\xi_l\vert}e^{i\lambda x\cdot(\xi_j-\xi_l)}\cdot\lambda^{k\alpha}\cdot\lambda\notag\\&\quad\times\partial_v^{(k+1)}(a^{2}(\lambda^\alpha \vert x\vert))\,dx\notag\\ &=\int{\bigg(\frac{-1}{i\lambda\vert\xi_j-\xi_l\vert}\bigg)^{k+1}e^{i\lambda x\cdot(\xi_j-\xi_l)}\lambda^{(k+1)\alpha}\partial_v^{(k+1)}(a^{2}(\lambda^\alpha \vert x\vert))\,dx}.\notag \end{align*} $$

Therefore, by the principle of mathematical induction, equation (2-5) is true for all n in $\mathbb {N}$ . This means that

$$ \begin{align*} \bigg\lvert\int{a^{2}(\lambda^\alpha\vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg\rvert &=\bigg\lvert\int{\bigg(\frac{-1}{i\lambda\vert\xi_j-\xi_l\vert}\bigg)^ne^{i\lambda x\cdot(\xi_j-\xi_l)}\lambda^{n\alpha}\partial_v^{(n)}(a^{2}(\lambda^\alpha \vert x\vert))\,dx}\bigg\rvert\notag\\ &\leq\int{\bigg\lvert\bigg(\frac{-1}{i\lambda\vert\xi_j-\xi_l\vert}\bigg)^ne^{i\lambda x\cdot(\xi_j-\xi_l)}\lambda^{n\alpha}\partial_v^{(n)}(a^{2}(\lambda^\alpha \vert x\vert))\bigg\rvert \,dx}\notag\\ &=\int{\frac{\lambda^{n\alpha}}{\lambda^n\vert\xi_j-\xi_l\vert^n}\vert\partial_v^{(n)}(a^{2}(\lambda^\alpha \vert x\vert))\vert \,dx}.\notag \end{align*} $$

Since the cut-off function has compact support, on the ball of radius $r=2\lambda ^{-\alpha }$ , and since the integrand is positive we can get an upper bound by taking the region of integration to be $\vert x\vert \leq 2\lambda ^{-\alpha }$ , and by letting $C_n$ be a positive constant that bounds the derivatives of $a^2_\lambda $ :

$$ \begin{align*}\bigg\lvert\int{a^{2}(\lambda^\alpha\vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg\rvert\leq\frac{\lambda^{n(-1+\alpha)}}{\vert\xi_j-\xi_l\vert^n}\int_{\vert x\vert\leq2\lambda^{-\alpha}}{C_n\,dx},\end{align*} $$

$$ \begin{align*}\bigg\lvert\int{a^{2}(\lambda^\alpha\vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg\rvert\leq C_n\bigg(\frac{\lambda^{-1+\alpha}}{\vert\xi_j-\xi_l\vert}\bigg)^n\int_{\vert x\vert\leq2\lambda^{-\alpha}}{1\,dx}.\end{align*} $$

The volume of this region is $4\pi \lambda ^{-2\alpha }$ , where the constants that are independent of $\lambda $ can be absorbed into $C_n$ :

$$ \begin{align*}\bigg\lvert\int{a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg\rvert\leq C_n\lambda^{-2\alpha}\bigg(\frac{\lambda^{-1+\alpha}}{\vert\xi_j-\xi_l\vert}\bigg)^n.\end{align*} $$

This concludes the proof.

From this we can see that the absolute value of the integral decays with $\lambda ^{-1+\alpha }$ and that for high frequencies, corresponding to large values of $\lambda $ , this means the integral has a small value. This upper bound is only effective if the factor that appears with each integration by parts is less than one, otherwise it increases the value each time, that is, ${\lambda ^{-1+\alpha }}/{\vert \xi _j-\xi _l\vert }<1$ . If this is not the case, that is, $\lambda ^{-1+\alpha }\geq \vert \xi _j-\xi _l\vert $ , then the oscillations are occurring at a low frequency, since the smallness of $\vert \xi _j-\xi _l\vert $ counteracts the rapid oscillations due to large values of $\lambda $ . This means that there will not be much cancellation due to oscillations, so one can obtain an effective upper bound using

$$ \begin{align*} \bigg\lvert\int{a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg\rvert&\leq\int{\lvert a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\rvert \,dx}\\&=\int{\vert a^2(\lambda^\alpha \vert x\vert)\vert \,dx} \leq \int_{\vert x\vert\leq2\lambda^{-\alpha}}{C_n\,dx}\\&\leq C_n\mathrm{Vol}(B_{2\lambda^{-\alpha}}(0))\leq C_n\lambda^{-2\alpha}, \end{align*} $$

where the constants that do not depend on $\lambda $ have been absorbed into $C_n$ (bounds on the derivatives of $a^2_\lambda $ ).

Both these cases can be combined and written as the following equation, which holds for all $n\in \mathbb {N}$ :

(2-6) $$ \begin{align} \bigg\lvert\int{a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg\rvert\leq C_n\lambda^{-2\alpha}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-n}. \end{align} $$

This works in the case where ${\lambda ^{-1+\alpha }}/{\vert \xi _j-\xi _l\vert }\leq 1$ since in this case ${\vert \xi _j-\xi _l\vert }/{\lambda ^{-1+\alpha }}\geq 1$ , meaning that this term is the dominant term in the expression, (2-6), for the bound, and the 1 can be ignored, giving the same bound as before. Similarly, if ${\lambda ^{-1+\alpha }}/{\vert \xi _j-\xi _l\vert }>1$ , one has that ${\vert \xi _j-\xi _l\vert }/{\lambda ^{-1+\alpha }}<1$ , meaning the 1 is the dominant term in (2-6), and the other term can be ignored. This also gives the correct bound for the second case.

For a fixed, finite, positive integer n, which is sufficiently large to cancel out the decay in $\lambda $ , one can pick $C=\max \{C_m\vert m\leq n\}$ since $a^2_\lambda $ is smooth, so its derivatives are all bounded. This implies

(2-7) $$ \begin{align} \int{a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}&\leq C_n\lambda^{-2\alpha}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-n}\nonumber\\&\leq C\lambda^{-2\alpha}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-n}. \end{align} $$

To be able to find an upper bound for the expectation (2-3), we need to find an upper bound for the double sum $\sum _{j,l,\ j\neq l} \int {a^2(\lambda ^\alpha \vert x\vert )e^{i\lambda x\cdot (\xi _j-\xi _l)}\,dx}$ . By fixing a value of j, the bounds determined above, (2-7), can be used to find an upper bound for the sum $\sum _{l,\ l\neq j} \int {a(\lambda ^\alpha \vert x\vert )e^{i\lambda x\cdot (\xi _j-\xi _l)}\,dx}$ :

(2-8) $$ \begin{align} \sum_{\substack{l\\ 1\neq j}}\int{a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\leq C\lambda^{-2\alpha}\sum_{\substack{l\\ 1\neq j}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-n}. \end{align} $$

Since there is a main region in which the integral is large, and then a decay in its size in the surrounding regions, we use a dyadic decomposition of the unit circle to find the upper bound. This will take into account the different contributions from the integrals as ${\lambda ^{-1+\alpha }}/{\vert \xi _j-\xi _l\vert }$ changes size.

Lemma 2.3. For the set of $N=\lambda \gamma $ equally distributed $\xi _l$ on the unit circle, where $\xi _j$ is fixed,

$$ \begin{align*}\sum_{\substack{l\\l\neq j}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}\leq \tilde C_{A}\gamma\lambda^\alpha\end{align*} $$

so long as $A\geq 2$ .

Proof. By splitting the unit circle, in which the direction vectors are contained, into dyadic regions, the sum over the $\xi _l$ can be turned into a geometric sum. The first region is the region where ${\lambda ^{-1+\alpha }}/{\vert \xi _j-\xi _l\vert }\geq 1$ (where integration by parts does not work to give the bound as the contributions are large). This region is a sector of the unit circle (which contains all the direction vectors within this sector), which is symmetrical about the direction vector $\xi _j$ . From the cosine rule ( $c^2=a^2+b^2-2ab \cos C$ ) we can calculate the relationship between the angle ( $\theta $ ) the sector spans (in one direction from $\xi _j$ ) and the length ( $\vert \xi _j-\xi _l\vert $ ) of the line connecting $\xi _j$ and $\xi _l$ ,. Since the lengths of the direction vectors, $\vert \xi _j\vert ,\vert \xi _l\vert $ , are one,

(2-9) $$ \begin{align} \vert\xi_j-\xi_l\vert^2&=1+1-2\cos\theta=2-2\cos\theta=4\sin^2\bigg(\frac{\theta}{2}\bigg), \nonumber\\ \vert\xi_j-\xi_l\vert&=2\sin\bigg(\frac{\theta}{2}\bigg). \end{align} $$

The angle is important since it determines how many direction vectors are in the regions, as they are spaced evenly around the circle. Since there are $N=\gamma \lambda $ direction vectors, their angular density is ${\gamma \lambda }/{2\pi }$ . From (2-9), $\theta =2\arcsin ({\vert \xi _j-\xi _l\vert }/{2})$ , which for purposes of simplicity can be overestimated by $\theta \leq 2\vert \xi _j-\xi _l\vert $ since $2\arcsin ({\vert \xi _j-\xi _l\vert }/{2})\leq 2\vert \xi _j-\xi _l\vert $ . This means that in this initial region where $\vert \xi _j-\xi _l\vert \leq \lambda ^{-1+\alpha }$ it follows that $\theta \leq 2\lambda ^{-1+\alpha }$ , and consequently there are $2\lambda ^{-1+\alpha }\cdot ({\gamma \lambda })/{2\pi }={\gamma \lambda ^\alpha }/{\pi }$ direction vectors in the sectors on either side of $\xi _j$ , meaning there are ${2\gamma \lambda ^\alpha }/{\pi }$ direction vectors in the first region. This overestimates the number of direction vectors in this region; however, since all the terms in the sum are positive this is acceptable for finding an upper bound.

The following regions are created by doubling the allowed sized of $\vert \xi _j-\xi _l\vert $ , meaning the regions are characterised by the sets $X_\beta $ , where each $X_\beta $ contains the $\xi _l$ that satisfy

$$ \begin{align*}2^{\beta-1}\lambda^{-1+\alpha}\leq\vert\xi_j-\xi_l\vert< 2^\beta\lambda^{-1+\alpha}.\end{align*} $$

The sum can be changed to a sum involving $\beta $ as an index, but it needs a maximum value of $\beta $ . We will denote this by B. Since we have that $\vert \xi _j-\xi _l\vert \leq 2$ , it follows that

$$ \begin{align*} 2&\leq2^B\lambda^{-1+\alpha},\\ \log(\lambda^{1-\alpha})&\leq(B-1)\log2,\\ \frac{\log(\lambda^{1-\alpha})}{\log2}+1&\leq B. \end{align*} $$

Therefore, we pick $B=\lceil {({\log (\lambda ^{1-\alpha })})/({\log 2})+1}\rceil $ since B must be a natural number, and overestimating it will only include repeated terms in the sum, which is all right for an upper bound, since the terms are all positive. The sum can now be rewritten as

$$ \begin{align*}\sum_{\substack{l\\ l\neq j}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}\leq \sum_{\beta=0}^B\sum_{\substack{l\\{\xi_l\in X_\beta}}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}.\end{align*} $$

Since the $\beta =0$ term is the main term of the sum, it is helpful to separate this from the others:

$$ \begin{align*}\notag \sum_{\substack{l\\l\neq j}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}\leq \sum_{\substack{l\\\vert\xi_j-\xi_l\vert\leq\lambda^{-1+\alpha}}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}+\sum_{\beta=1}^B\sum_{\substack{l\\\xi_l\in X_\beta}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}. \end{align*} $$

For the $\beta =0$ case the sum over l is ${2\gamma \lambda ^\alpha }/{\pi }$ , and since this is the case where ${\vert \xi _j-\xi _l\vert }/({\lambda ^{-1+\alpha }})$ is small, compared to 1, and can be ignored in the expression $1+{\vert \xi _j-\xi _l\vert }/({\lambda ^{-1+\alpha }})$ , the first term becomes

$$ \begin{align*}\sum_{\substack{l\\\vert\xi_j-\xi_l\vert\leq\lambda^{-1+\alpha}}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}\lesssim\frac{2\gamma\lambda^\alpha}{\pi}\cdot 1^{-A}=\hat{C_0}\gamma\lambda^{\alpha}.\end{align*} $$

For the following terms, we use the same way of estimating the number of direction vectors in each sector, as for the first region: $\theta \leq 2\vert \xi _j-\xi _l\vert $ . For the region with the outer boundary at $\vert \xi _j-\xi _l\vert =2^\beta \lambda ^{-1+\alpha }$ , this means that the boundary angle satisfies $\theta \leq 2^{\beta +1}\lambda ^{-1+\alpha }$ . As in the first region, this is overestimating the angle. The total number of direction vectors in that sector is $({\lambda \gamma }/{2\pi })\cdot 2\cdot 2^{\beta +1}\lambda ^{-1+\alpha }={2^{\beta +1}\gamma \lambda ^{\alpha }}/{\pi }$ , where the factor of two accounts for the angle going in both directions. (This counts all the direction vectors up to the boundary in each term, repeating the previous sections’ ones, which is not a problem for an upper bound.) This evaluates the sum over l for each value of  $\beta $ . Through overestimation of the $1-{\vert \xi _j-\xi _l\vert }/({\lambda ^{-1+\alpha }})$ term, based on which set $X_\beta $ the $\xi _l$ is in, the second term becomes

$$ \begin{align*}\sum_{\beta=1}^B\sum_{\substack{l\\\xi_l\in X_\beta}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}\leq\sum_{\beta=1}^B\sum_{l}(1+2^{\beta-1})^{-A}.\end{align*} $$

Evaluating the sum over l for each $\beta $ gives

$$ \begin{align*}\sum_{\beta=1}^B\sum_{\substack{l\\\xi_l\in X_\beta}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}\lesssim\frac{\gamma\lambda^\alpha}{\pi}\sum_{\beta=1}^B2^{\beta+1}(1+2^{\beta-1})^{-A}.\end{align*} $$

Since $\beta $ is bigger than 1, the $2^{\beta -1}$ term will be dominant compared to 1 in $(1+2^{\beta -1})$ :

$$ \begin{align*} \sum_{\beta=1}^B\sum_{\substack{l\\\xi_l\in X_\beta}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}\lesssim\frac{\gamma\lambda^{\alpha}}{\pi}\sum_{\beta=1}^B2^{A+1}2^{\beta(1-A)}=\frac{2^{A+1}\gamma\lambda^{\alpha}}{\pi}\sum_{\beta=1}^B2^{\beta(1-A)}.\end{align*} $$

Since $A\geq 2$ the geometric sum has a ratio ( $2^{1-A}$ ) that is less than 1, so the series converges and the sum is bounded above. The sum starts at $\beta =1$ so the infinite sum converges to ${r}/({1-r})$ and $\sum _{\beta =1}^B2^{\beta (1-A)}$ is bounded above by ${2^{1-A}}/({1-2^{1-A}})$ , giving

$$ \begin{align*}\sum_{\beta=1}^B\sum_{\substack{l\\\xi_l\in X_\beta}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}\leq\frac{2^{A+1}2^{1-A}\gamma\lambda^{\alpha}}{(1-2^{1-A})\pi}=\hat{C}\gamma\lambda^{\alpha}.\end{align*} $$

Therefore, adding the $\beta =0$ term and the other terms together,

$$ \begin{align*}\sum_{\substack{l\\l\neq j}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-A}\lesssim\hat{C_0}\gamma\lambda^\alpha+\hat{C}\gamma\lambda^\alpha=\tilde C_A\gamma\lambda^{\alpha}.\end{align*} $$

This concludes the proof.

We can now return to the expression for the sums in the expectation, (2-8), and use the above result to estimate the contribution from the off-diagonal terms to the expectation value.

From the lemma above and (2-8),

$$ \begin{align*}\sum_{\substack{l\\l\neq j}}\int{a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\lesssim C\lambda^{-2\alpha}\cdot \tilde C_n\gamma\lambda^\alpha= K\gamma\lambda^{-\alpha}\end{align*} $$

(as long as the chosen fixed n satisfies $n\geq 2$ ).

Since this upper bound was not dependent on the $\xi _j$ that was fixed, it will hold for all $\xi _j$ , and hence the sum over j can be evaluated by multiplying by $N=\gamma \lambda $ , giving

$$ \begin{align*}\sum_{\substack{j,l\\j\neq l}}\int{a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\lesssim K\gamma^2\lambda^{1-\alpha}.\end{align*} $$

Substituting this bound for the double sum into (2-3), the expression for the expectation gives us the following final upper bound for the expectation value:

(2-10) $$ \begin{align} \mathbb{E}(\lVert a_\lambda u\rVert^2)\leq4\pi\gamma\lambda^{1-2\alpha}+K(2p-1)^2\gamma^2\lambda^{1-\alpha}. \end{align} $$

Equidistribution. When the coefficients of the random wave are determined by a fair coin (that is, the probability of $C_j=+1$ is 0.5 and is equal to the probability of $C_j=-1$ ) the expectation has the same size as the volume of the region (once it has been normalised). This property of equidistribution is interesting, and so we look for probabilities, p, where this property holds. Looking at (2-10), this property holds if the two terms are the same size (since the first term is the expectation value for $p=0.5$ ). In this case $\gamma \simeq 1$ so the terms are the same size when

$$ \begin{align*} (2p-1)^2\lambda^{1-\alpha}&=\mathcal{O}(\lambda^{1-2\alpha}),\\ (2p-1)^2&=\mathcal{O}(\lambda^{-\alpha}),\\ 2p-1&=\mathcal{O}(\lambda^{-{\alpha}/{2}}),\\ p&=0.5+\mathcal{O}(\lambda^{-{\alpha}/{2}}). \end{align*} $$

This means that, up to constants, if the probability is $\lambda ^{-{\alpha }/{2}}$ close to 0.5, the expectation will have the same size as the volume of the region. This is summarised in the following corollary.

Corollary 2.4. A random wave given by (1-1) where the coefficients are determined by an unfair coin ( $C_j=+1$ has probability p and $C_j=-1$ has probability $1-p$ ), and where $\gamma \simeq 1$ , has the property that

$$ \begin{align*}\mathbb{E}(\lVert a_\lambda u\rVert^2)\leq C\mathrm{Vol}(B_{\lambda^{-\alpha}}(0))\end{align*} $$

if

$$ \begin{align*}\lvert p-0.5\rvert\lesssim\lambda^{-{\alpha}/{2}}.\end{align*} $$

3 Proof of Theorem 1.2

In this section we use a different approach to get both a lower bound and an upper bound for the expectation. Each sum we are trying to evaluate has terms that come from a single function, which means that approximating the sums by integrals becomes a likely way to get bounds on the sum. Therefore, to find bounds for the expectation, we use a Darboux integral based approach where we assume that $\gamma $ (the parameter that controls the number of direction vectors) is large, possibly tending to infinity.

From (2-2) the sum, in the expression for the expectation, which needs to be evaluated is

$$ \begin{align*}S=\sum_{j,l}\int{a^{2}(\lambda^\alpha}\vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)\,dx}=\int{a^{2}(\lambda^\alpha \vert x\vert)\sum_je^{i\lambda x\cdot\xi_j}\sum_l e^{-i\lambda x\cdot\xi_l}\,dx}.\end{align*} $$

The sum over $\xi _l$ can be parametrised using $\theta _l$ as the angle between x and $\xi _l$ , where x is fixed. $\theta _l$ is chosen so that $\theta =0$ coincides with $\xi _l={x}/{\vert x\vert }$ and $\theta _l\in [-\pi ,\pi )$ . Similarly, the sum over $\xi _j$ can be parametrised using $\theta _j$ as the angle between $\xi _j$ and x where x is fixed. $\theta _j$ is chosen so that $\theta =0$ coincides with $\xi _j={x}/{\vert x\vert }$ and $\theta _j\in [-\pi ,\pi )$ . Since the direction vectors are equally spaced around the unit circle, the width of the interval between two consecutive $\theta _l$ or $\theta _j$ is ${2\pi }/{\gamma \lambda }$ . The sum can thus be expressed as

(3-1) $$ \begin{align} S=\int{a^{2}(\lambda^\alpha \vert x\vert)\sum_je^{i\lambda \vert x\vert\cos\theta_j}\sum_l e^{-i\lambda \vert x\vert\cos\theta_l}\,dx}. \end{align} $$

We now want to turn these sums over j, l into integrals over $\theta $ . The following lemma gives us the ability to do so.

Lemma 3.1. For sums of the form $\sum _lf(\theta _l)$ , where the $\theta _l$ are evenly spaced with a spacing of ${2\pi }/{\gamma \lambda }$ and $\theta _l\in [-\pi ,\pi )$ , and where $f(\theta )$ is a continuous function that satisfies $\vert f'(\theta )\vert \lesssim \lambda ^{1-\alpha }$ ,

$$ \begin{align*}\frac{2\pi}{\gamma\lambda}\sum_lf(\theta_l) \to \int_{-\pi}^\pi f(\theta)\,d\theta\quad \text{ as }\gamma\to\infty.\end{align*} $$

Proof. To be able to turn the sum into a Darboux integral, let $P=\{-\pi ,\pi \}\cup \{\text {set of }\theta _l\}$ be a partition. Due to the even spacing of the $\theta _l$ , the distance between the $\theta _1$ and $-\pi $ or $\theta _N$ and $\pi $ is less than ${2\pi }/{\gamma \lambda }$ , as otherwise there would be another $\theta _l$ in between. We use the standard notation for Darboux sums: $m_i=\inf \{f(\theta )\vert \theta \in [\theta _i,\theta _{i+1}]\}$ , $M_i=\sup \{f(\theta )\vert \theta \in [\theta _i,\theta _{i+1}]\}$ , $L(f)=\sum _i\Delta \theta _im_i$ and $U(f)=\sum _i\Delta \theta _iM_i$ . Since the function $f(\theta )$ is continuous, it will attain its maximum and minimum on the interval $[\theta _i,\theta _{i+1}]$ . To calculate $m_i$ and $M_i$ for each interval, we use a linear Taylor approximation about $\theta _i$ on each interval, where $\hat {\theta }\in [\theta _i,\theta _{i+1}]$ :

$$ \begin{align*}f(\theta)=f(\theta_i)+f'(\hat{\theta})(\theta-\theta_i).\end{align*} $$

In each interval we have $\theta -\theta _i\leq {2\pi }/{\gamma \lambda }$ . This means that on the interval $[\theta _i,\theta _{i+1}]$ , we can write $f(\theta )=f(\theta _i)+\mathcal {O}(\gamma ^{-1}\lambda ^{-\alpha })$ . As this is true for any $\theta $ in the interval, it will be true for the values of $\theta $ that give the maximum and minimum values of f: $m_i=f(\theta _i)+\mathcal {O}(\gamma ^{-1}\lambda ^{-\alpha })$ and $M_i=f(\theta _i)+\mathcal {O}(\gamma ^{-1}\lambda ^{-\alpha })$ . Therefore, $M_i-m_i=\mathcal {O}(\gamma ^{-1}\lambda ^{-\alpha })$ . This is true for all $N+1$ intervals, meaning that

$$ \begin{align*}\notag U(f)-L(f)&=\sum_i (M_i-m_i)\Delta\theta_i\lesssim\sum_i\mathcal{O}(\gamma^{-1}\lambda^{-\alpha})\frac{2\pi}{\gamma\lambda}\\ &=(N+1)\mathcal{O}(\gamma^{-2}\lambda^{-1-\alpha})=\mathcal{O}(\gamma^{-1}\lambda^{-\alpha})+\mathcal{O}(\gamma^{-2}\lambda^{-1-\alpha}). \end{align*} $$

Since $\gamma ^{-1}\lambda ^{-\alpha }>\gamma ^{-2}\lambda ^{-1-\alpha }$ , the dominant error term is $\mathcal {O}(\gamma ^{-1}\lambda ^{-\alpha })$ , giving

$$ \begin{align*}0\leq U(f)-L(f)\lesssim\mathcal{O}(\gamma^{-1}\lambda^{-\alpha}).\end{align*} $$

When $\gamma \rightarrow \infty $ this tends to zero, and hence the upper and lower Darboux sums are equal to each other in the limit.

Now, for any partition,

$$ \begin{align*}L(f)\leq\int_{-\pi}^{\pi}f(\theta)\,d\theta\leq U(f),\end{align*} $$

so, by the squeeze theorem, the upper and lower Darboux sums are equal to the Darboux integral in the limit as $\gamma $ gets large.

We will now see that $L(f)\leq C_{\lambda \gamma }\sum _lf(\theta _l)\leq U(f)$ (and in fact calculate $C_{\lambda \gamma }$ ), so that we can apply the squeeze theorem. On the intervals of the form $[\theta _l,\theta _{l+1}]$ (of which there are $N-1$ ), we can use the estimates $M_l\geq f(\theta _l)$ and $m_l\leq f(\theta _l)$ . For these intervals $\Delta \theta _l={2\pi }/{\lambda \gamma }$ . On the interval $[\theta _N,\pi ]$ , we can use the estimates $M_N\geq f(\theta _N)$ and $m_N\leq f(\theta _N)$ . For this interval the width is $\Delta \theta _N\simeq k_N\cdot {2\pi }/{\lambda \gamma }$ . On the interval $[-\pi , \theta _1]$ , using a Taylor expansion about the point $\theta _1$ gives $M_0\geq f(\theta _1)$ , and similarly $m_0\leq f(\theta _1)$ . The width of this interval is $\Delta \theta _0\simeq k_1\cdot {2\pi }/{\gamma \lambda }$ .

Therefore, we obtain the following bounds:

$$ \begin{align*} U(f)\geq\sum_{j=1}^{N-1}f(\theta_j)\cdot\frac{2\pi}{\gamma\lambda}+f(\theta_1)k_1\frac{2\pi}{\gamma\lambda}+f(\theta_N)k_N\frac{2\pi}{\gamma\lambda}=\frac{2\pi}{\gamma\lambda}\sum_{j=1}^Nf(\theta_j)+\mathcal{O}(\gamma^{-1}\lambda^{-1})\end{align*} $$

and

$$ \begin{align*}L(f)\leq\sum_{j=1}^{N-1}f(\theta_j)\cdot\frac{2\pi}{\gamma\lambda}+f(\theta_1)k_1\frac{2\pi}{\gamma\lambda}+f(\theta_N)k_N\frac{2\pi}{\gamma\lambda}=\frac{2\pi}{\gamma\lambda}\sum_{j=1}^Nf(\theta_j)+\mathcal{O}(\gamma^{-1}\lambda^{-1}),\end{align*} $$

which can be written together to give

$$ \begin{align*}L(f)\leq\frac{2\pi}{\gamma\lambda}\sum_{j=1}^Nf(\theta_j)+\mathcal{O}(\gamma^{-1}\lambda^{-1})\leq U(f).\end{align*} $$

Now let $\epsilon>0$ . Then we can pick $\Gamma $ so that if $\gamma \geq \Gamma $ , then $\lvert \mathcal {O}(\gamma ^{-1}\lambda ^{-1})\rvert \leq \epsilon .$ This is possible as the error term is converging as $\gamma ^{-1}$ . From this,

$$ \begin{align*}L(f)\leq\frac{2\pi}{\gamma\lambda}\sum_{l=1}^Nf(\theta_l)\pm\epsilon\leq U(f),\end{align*} $$

$$ \begin{align*}L(f)-\epsilon\leq\frac{2\pi}{\gamma\lambda}\sum_{l=1}^Nf(\theta_l)\leq U(f)+\epsilon.\end{align*} $$

Since this is true for all $\epsilon>0$ , it follows that

$$ \begin{align*}L(f)\leq\frac{2\pi}{\gamma\lambda}\sum_{l=1}^\infty f(\theta_l)\leq U(f).\end{align*} $$

Taking the limit as $\gamma \rightarrow \infty $ and using the squeeze theorem gives

$$ \begin{align*}\lim_{\gamma\to\infty}\frac{2\pi}{\gamma\lambda}\sum_lf(\theta_l)=\int_{-\pi}^\pi f(\theta)\,d\theta.\end{align*} $$

This concludes the proof.

To use this lemma to evaluate the sums in the expression for the expectation, (3-1), we need to show that the bound on the derivative of the functions holds. In this case $f(\theta )=e^{\pm i\lambda \vert x\vert \cos \theta }$ . Due to the size of the region of integration, $\vert x\vert \lesssim \lambda ^{-\alpha }$ . This means that

$$ \begin{align*} f'(\theta)&=\pm i\lambda\vert x\vert\sin\theta\cdot e^{\pm i\lambda \vert x\vert\cos\theta},\\ \lvert f'(\theta)\rvert&=\lvert \pm i\lambda\vert x\vert\sin\theta\cdot e^{\pm i\lambda \vert x\vert\cos\theta}\rvert\leq \lambda\vert x\vert\lesssim \lambda^{1-\alpha}. \end{align*} $$

Therefore, we use Lemma 3.1 on the sums in (3-1) to obtain

$$ \begin{align*} \lim_{\gamma\to\infty}\frac{2\pi}{\gamma\lambda}\sum e^{-i\lambda\vert x\vert\cos\theta_l}=\int_{-\pi}^{\pi}{e^{-i\lambda\vert x\vert\cos\theta}\,d\theta} \end{align*} $$

and

$$ \begin{align*} \lim_{\gamma\to\infty}\frac{2\pi}{\gamma\lambda}\sum e^{i\lambda\vert x\vert\cos\theta_j}=\int_{-\pi}^{\pi}{e^{i\lambda\vert x\vert\cos\theta}\,d\theta}. \end{align*} $$

We also want to obtain a rate for the convergence in $\gamma $ . In particular, we want to write

$$ \begin{align*}\notag &\int a^{2}(\lambda^\alpha \vert x\vert)\sum_{j,l}e^{i\lambda\vert x\vert(\cos(\theta_{j})-\cos(\theta_{l}))}\,dx\\ &\quad=\frac{\gamma^{2}\lambda^{2}}{4\pi^{2}}\int a^{2}(\lambda^{\alpha}\vert x\vert)\bigg[\bigg(\int_{-\pi}^{\pi} e^{i\lambda\vert x\vert\cos\theta}\,d\theta\bigg)\bigg(\int_{-\pi}^{\pi}e^{-i\lambda\vert x\vert\cos\psi}\,d\psi\bigg)\bigg]\,dx+E_{\gamma} \end{align*} $$

and obtain bounds for $\vert E_{\gamma }\vert $ . If we write

$$ \begin{align*} \sum_{j}e^{i\lambda\vert x\vert\cos(\theta_{j})}&=I_{1}(x)+E_{1}(x),\\ \sum_{l}e^{-i\lambda\vert x\vert\cos(\theta_{l})}&=I_{2}(x)+E_{2}(x), \end{align*} $$

where $I_{1}(x)$ and $I_{2}(x)$ represent the integrals and $E_{1}(x),E_{2}(x)$ the errors, then

$$ \begin{align*}\notag &\bigg\vert\int a^{2}(\lambda^\alpha \vert x\vert)\bigg(\sum_{j,l}e^{i\lambda\vert x\vert(\cos(\theta_{j})-\cos(\theta_{l}))}-I_{1}(x)I_{2}(x)\bigg)\,dx\bigg\vert\\ &\quad=\bigg\vert\int a^{2}(\lambda^\alpha \vert x\vert)(I_{1}(x)E_{2}(x)+I_{2}(x)E_{1}(x)+E_{1}(x)E_{2}(x))\,dx\bigg\vert\\ &\quad\leq |\!|{a_{\lambda}I_{1}}|\!|_{L^{2}}|\!|{a_{\lambda}E_{2}}|\!|_{L^{2}}+|\!|{a_{\lambda}I_{2}}|\!|_{L^{2}}|\!|{a_{\lambda}E_{1}}|\!|_{L^{2}}+|\!|{a_{\lambda}E_{1}}|\!|_{L^{2}}|\!|{a_{\lambda}E_{2}}|\!|_{L^{2}}, \end{align*} $$

where we have applied Cauchy–Schwarz to obtain the last line.

So we need to obtain control on $|\!|{I_{1}}|\!|_{L^{2}}$ , $|\!|{I_{2}}|\!|_{L^{2}}$ , $|\!|{E_{1}}|\!|_{L^{2}}$ and $|\!|{E_{2}}|\!|_{L^{2}}$ . The control on the $L^{2}$ norms coming from $I_{1}(x)$ and $I_{2}(x)$ will follow from the stationary phase computation we use to compute the $I_{1}(x)I_{2}(x)$ term. That just leaves the error terms. We can estimate them using much the same argument as we developed in Theorem 2.2 and Lemma 2.3.

Lemma 3.2. Suppose the error terms are given by

$$ \begin{align*} E_{1}(x)&=\sum_{j}e^{i\lambda\vert x\vert\cos(\theta_{j})}-\frac{\gamma\lambda}{2\pi}\int_{-\pi}^{\pi}e^{i\lambda\vert x\vert\cos(\theta)}\,d\theta=\sum_{j}e^{i\lambda\vert x\vert\cos(\theta_{j})}-\frac{\gamma\lambda}{2\pi}\int_{\mathbb{S}}e^{i\lambda x\cdot \xi}\,d\mu(\xi),\\ E_{2}(x)&=\sum_{l}e^{-i\lambda\vert x\vert\cos(\theta_{l})}-\frac{\gamma\lambda}{2\pi}\int_{-\pi}^{\pi}e^{-i\lambda\vert x\vert\cos(\psi)}\,d\psi =\sum_{l}e^{i\lambda\vert x\vert\cos(\theta_{l})}-\frac{\gamma\lambda}{2\pi}\int_{\mathbb{S}}e^{i\lambda x\cdot \eta}\,d\mu(\eta). \end{align*} $$

Then

$$ \begin{align*} |\!|{a_{\lambda}E_{1}}|\!|_{L^{2}}&\lesssim\gamma\lambda^{{1}/{2}-{\alpha}/{2}},\\ |\!|{a_{\lambda}E_{2}}|\!|_{L^{2}}&\lesssim\gamma\lambda^{{1}/{2}-{\alpha}/{2}}.\end{align*} $$

Proof. We present the proof for $E_{1}$ (the proof for $E_{2}$ is identical). For $j=1,\dots ,N-1$ denote the arc of $\mathbb {S}$ lying between $\xi _{j}$ and $\xi _{j+1}$ by $\mathbb {S}_{j}$ and let $\mathbb {S}_{N}$ be the arc between $\xi _{N}$ and $\xi _{1}$ . We write

$$ \begin{align*}E_{1}(x)=\frac{\gamma\lambda}{2\pi}\sum_{j}\int_{\mathbb{S}_{j}}e^{i\lambda x\cdot \xi_{j}}\,d\mu(\xi)-\sum_{j}\int_{\mathbb{S}_{j}}e^{i\lambda x\cdot \xi}\,d\mu(\xi).\end{align*} $$

Note that, as we saw in the proof of Lemma 3.1, a Taylor expansion of the exponential in $\xi $ around $\xi _{j}$ would give an estimate of

$$ \begin{align*}\vert E_{1}(x)\vert\lesssim\lambda^{1-\alpha}.\end{align*} $$

However, by exploiting the oscillatory nature of the x integrals, we are able to improve on this. Expanding $\vert E_{1}(x)\vert ^{2}$ , we have that

$$ \begin{align*} \int a^{2}(\lambda^\alpha \vert x\vert)\vert E_{1}(x)\vert^{2}\,dx &=\bigg(\frac{\gamma\lambda}{2\pi}\bigg)^{2}\sum_{j,l}\bigg(\int_{\mathbb{S}_{j}}\int_{\mathbb{S}_{l}}\int a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot (\xi_{j}-\xi_{l})}\,dx\,d\mu(\xi)\,d\mu(\eta) \\ &\quad-\int_{\mathbb{S}_{j}}\int_{\mathbb{S}_{l}}\int a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_{j}-\eta)}\,dx\,d\mu(\xi)\, d\mu(\eta)\\ &\quad-\int_{\mathbb{S}_{j}}\int_{\mathbb{S}_{l}}\int a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi-\xi_{l})}\,dx\,d\mu(\xi)\,d\mu(\eta)\\ &\quad+\int_{\mathbb{S}_{j}}\int_{\mathbb{S}_{l}}\int a^{2}(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot (\xi-\eta)}\,dx \,d\mu(\xi)\,d\mu(\eta)\bigg).\end{align*} $$

Now we can apply the integration by parts arguments of Theorem 2.2 to each term separately. Then using a Taylor expansion, and the fact that $\vert \xi -\xi _{j}\vert \leq 2\pi \lambda ^{-1}\gamma ^{-1}$ and $\vert \eta -\xi _{l}\vert \leq 2\pi \lambda ^{-1}\gamma ^{-1}$ , we obtain

$$ \begin{align*}\int a^{2}(\lambda^\alpha \vert x\vert)\vert E_{1}(x)\vert^{2}\leq C_{n}\frac{\lambda^{-2\alpha}}{\gamma}\sum_{j,l}\bigg(1+\frac{\vert\xi_{j}-\xi_{l}\vert}{\lambda^{-1+\alpha}}\bigg)^{-n}.\end{align*} $$

Finally, we use the same dyadic decomposition of Lemma 2.3 to obtain

$$ \begin{align*}\int a^{2}(\lambda^\alpha \vert x\vert)\vert E_{1}(x)\vert^{2}\leq CN\lambda^{-\alpha}=C\gamma\lambda^{1-\alpha},\end{align*} $$

yielding the estimate

$$ \begin{align*}|\!|{a_{\lambda}E_{1}}|\!|_{L^{2}}\lesssim \gamma^{{1}/{2}} \lambda^{{1}/{2}-{\alpha}/{2}}.\end{align*} $$

This concludes the proof.

We now compute $I_{1}(x)$ and $I_{2}(x)$ . With these in hand we can compute

$$ \begin{align*}\int a^{2}(\lambda^{\alpha}\vert x\vert)I_{1}(x)I_{2}(x)\,dx\end{align*} $$

and estimate $|\!|{I_{1}}|\!|_{L^{2}}$ and $|\!|{I_{2}}|\!|_{L^{2}}$ . We will do this by applying the method of stationary phase to the angular oscillatory integrals. We first consider the case $\vert x\vert>\lambda ^{-1}$ , since this allows us to look only at the leading terms in the expansions.

Lemma 3.3. If $\vert x\vert $ is greater than $\lambda ^{-1}$ , then it follows that

$$ \begin{align*}\int_{-\pi}^\pi e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta\simeq2\sqrt{2\pi}(\lambda\vert x\vert)^{-{1}/{2}}\cos\bigg(\lambda\vert x\vert-\frac{\pi}{4}\bigg)+\mathcal{O}((\lambda\vert x\vert)^{-{3}/{2}}).\end{align*} $$

Proof. This lemma is a standard result about Bessel functions using the asymptotic form, as

$$ \begin{align*} \int_{-\pi}^\pi e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta=2\pi J_0(\lambda\vert x\vert)\simeq2\sqrt{2\pi}(\lambda\vert x\vert)^{-{1}/{2}}\cos\bigg(\lambda\vert x\vert-\frac{\pi}{4}\bigg)+\mathcal{O}((\lambda\vert x\vert)^{-{3}/{2}}). \end{align*} $$

However, we include an alternate proof using the method of stationary phase.

We will use the method of stationary phase outlined in the SEGwiki [7] to approximate the integral. To avoid having to deal with boundary terms, we introduce the smooth cut-off functions $b_1(\theta )$ that satisfy $b_1(\theta )=1$ when $\theta \in [-{\pi }/{4},{\pi }/{4}]$ , and have compact support on $[-{\pi }/{2},{\pi }/{2}]$ and $b_2(\theta )=1-b_1(\theta )$ . These cut-off functions allow us to rewrite the integral as

(3-2) $$ \begin{align}\notag \int_{-\pi}^{\pi}e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta&=\int_{-\pi}^{\pi}b_1(\theta)e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta+\int_{-\pi}^{\pi}b_2(\theta)e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta\\\notag &=\int_{-{\pi}/{2}}^{{\pi}/{2}}b_1(\theta)e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta+\int_{-\pi}^{-{\pi}/{4}}b_2(\theta)e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta\\&\quad+\int_{{\pi}/{4}}^{\pi}b_2(\theta)e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta. \end{align} $$

The stationary points are the points where the phase function $\phi (\theta )=\pm \cos \theta $ satisfies $\phi '(\theta )=\mp \sin \theta =0$ , which in this case are $\theta =0,\pm \pi $ . This means for the first integral in (3-2) the stationary point is an interior stationary point, for the second interval the stationary point is at the lower endpoint of the integration and for the last integral the stationary point is at the upper endpoint of integration. There are three different formulas for these three cases, see [7].

Interior stationary point. For a stationary point at $t=c$ , where $a<c<b$ ,

$$ \begin{align*}\int_a^bf(t)e^{i\lambda\phi(t)}\,dt\simeq e^{i\lambda\phi(c)+i\text{sgn}(\phi''(c))\cdot{\pi}/{4}}f(c)\sqrt{\frac{2\pi}{\lambda\vert\phi''(c)\vert}}+\mathcal{O}(\lambda^{-{3}/{2}}).\end{align*} $$

In this case $\lambda =\lambda \vert x\vert $ , $\phi (x)=\pm \cos \theta $ , $f(t)=b_1(\theta )$ , $a=-{\pi }/{2}$ , $b={\pi }/{2}$ and $c=0$ . Noting that $b_1(0)=1$ , this gives

(3-3) $$ \begin{align} \int_{-\pi}^{\pi}b_1(\theta)e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta\simeq e^{\pm i\lambda\vert x\vert\mp i\cdot{\pi}/{4}}\sqrt{\frac{2\pi}{\lambda\vert x\vert}}+\mathcal{O}((\lambda\vert x\vert)^{-{3}/{2}}). \end{align} $$

Lower endpoint of integration. For a stationary point at $t=a$ ,

$$ \begin{align*} \int_a^b{f(t)e^{i\lambda \phi(t)}\,dt}&\simeq \frac12e^{i\lambda\phi(a)+i\text{sgn}(\phi''(a))\pi/4}\left\{f(a)\sqrt{\frac{2\pi}{\lambda\vert\phi''(a)\vert}}\right.\\&\quad\left.+\,\frac{2}{\lambda\vert\phi''(a)\vert}\bigg[f'(a)-\frac{\phi'''(a)}{3\vert\phi''(a)\vert}\bigg]e^{i\lambda\text{sgn}(\phi''(a))\pi/4}\vphantom{\sqrt{\frac{2\pi}{\lambda\vert\phi''(a)\vert}}}\right\}+\mathcal{O}(\lambda^{-{3}/{2}}).\end{align*} $$

In this case, $\lambda =\lambda \vert x\vert $ , $\phi (x)=\pm \cos \theta $ , $f(t)=b_2(\theta )$ , $a=-\pi $ and $b=-{\pi }/{4}$ . Noting that $b_2(-\pi )=1$ , $b_2'(-\pi )=0$ and $\phi '''(a)=\pm \sin (-\pi )=0$ , this gives

(3-4) $$ \begin{align} \int_{-\pi}^{-{\pi}/{4}}b_2(\theta)e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta\simeq\frac12e^{\mp i\lambda\vert x\vert\pm i\pi/4}\sqrt{\frac{2\pi}{\lambda\vert x\vert}}+\mathcal{O}((\lambda\vert x\vert)^{-{3}/{2}}). \end{align} $$

Upper endpoint of integration. For a stationary point at $t=b$ ,

$$ \begin{align*} \int_a^b{f(t)e^{i\lambda \phi(t)}\,dt}&\simeq \frac12e^{i\lambda\phi(b)+i\text{sgn}(\phi''(b))\pi/4}\left\{f(b)\sqrt{\frac{2\pi}{\lambda\vert\phi''(b)\vert}}\right.\\&\quad\left.-\frac{2}{\lambda\vert\phi''(b)\vert}\bigg[f'(b)-\frac{\phi'''(b)}{3\vert\phi''(b)\vert}\bigg]e^{i\lambda\text{sgn}(\phi''(b))\pi/4}\vphantom{\sqrt{\frac{2\pi}{\lambda\vert\phi''(b)\vert}}}\right\}+\mathcal{O}(\lambda^{-{3}/{2}}). \end{align*} $$

In this case, $\lambda =\lambda \vert x\vert $ , $\phi (x)=\pm \cos \theta $ , $f(t)=b_2(\theta )$ , $a={\pi }/{4}$ and $b=\pi $ . Noting that $b_2(\pi )=1$ , $b_2'(\pi )=0$ and $\phi '''(b)=\pm \sin (\pi )=0$ , this gives

(3-5) $$ \begin{align} \int_{\frac{\pi}{4}}^{\pi}b_2(\theta)e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta\simeq \frac12e^{\mp i\lambda\vert x\vert\pm i\pi/4}\sqrt{\frac{2\pi}{\lambda\vert x\vert}}+\mathcal{O}((\lambda\vert x\vert)^{-{3}/{2}}). \end{align} $$

Putting (3-3), (3-4) and (3-5) together gives us the overall integral:

$$ \begin{align*}\notag \int_{-\pi}^{\pi}e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta&\simeq e^{\pm i\lambda\vert x\vert\mp i{\pi}/{4}}\sqrt{\frac{2\pi}{\lambda\vert x\vert}}+\frac12e^{\mp i\lambda\vert x\vert\pm i\pi/4}\sqrt{\frac{2\pi}{\lambda\vert x\vert}}\\&\quad+\frac12e^{\mp i\lambda\vert x\vert\pm i\pi/4}\sqrt{\frac{2\pi}{\lambda\vert x\vert}}+\mathcal{O}((\lambda\vert x\vert)^{-{3}/{2}})\notag\\\notag &=e^{\pm i\lambda\vert x\vert\mp i{\pi}/{4}}\sqrt{\frac{2\pi}{\lambda\vert x\vert}}+e^{\mp i\lambda\vert x\vert\pm i\pi/4}\sqrt{\frac{2\pi}{\lambda\vert x\vert}}+\mathcal{O}((\lambda\vert x\vert)^{-{3}/{2}})\\\notag &=\sqrt{2\pi}(e^{\pm i(\lambda\vert x\vert-{\pi}/{4})}+e^{\mp i(\lambda\vert x\vert-{\pi}/{4})})(\lambda\vert x\vert)^{-{1}/{2}}+\mathcal{O}((\lambda\vert x\vert)^{-{3}/{2}})\notag\\ \notag &=2\sqrt{2\pi}(\lambda\vert x\vert)^{-{1}/{2}}\cos(\lambda\vert x\vert-{\pi}/{4})+\mathcal{O}((\lambda\vert x\vert)^{-{3}/{2}}). \end{align*} $$

This concludes the proof.

This method of estimating the integral only works if $\lambda \vert x\vert>1$ , as otherwise the later terms in the approximation will get very big. If this is not the case, and $\lambda \vert x\vert \leq 1$ , then the function is not oscillating a lot, so

$$ \begin{align*}\bigg\lvert\int_{-\pi}^{\pi}{e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta}\bigg\rvert\leq\int_{-\pi}^\pi\lvert e^{\pm i\lambda\vert x\vert\cos\theta}\rvert \,d\theta\leq\int_{-\pi}^\pi1\,d\theta= 2\pi\end{align*} $$

is an appropriate bound. From this we can see that, when $\lambda \vert x\vert \leq 1$ ,

(3-6) $$ \begin{align} \int_{-\pi}^{\pi}{e^{\pm i\lambda\vert x\vert\cos\theta}\,d\theta}=\mathcal{O}(1). \end{align} $$

We can now compute

$$ \begin{align*}I=\int a^{2}(\lambda^{\alpha}\vert x\vert)I_{1}(x)I_{2}(x)\,dx,\end{align*} $$

where we can replace the integrals with the approximations from Lemma 3.3 and equation (3-6). Since the approximations for the interior integrals depend on the size of $\lambda \vert x\vert $ , it is helpful to split the integral into two regions: $\vert x\vert \leq \lambda ^{-1}$ and $\vert x\vert>\lambda ^{-1}$ . The term $C\lambda ^{-{3}/{2}}\vert x\vert ^{-{3}/{2}}$ represents the $\mathcal {O}((\lambda \vert x\vert )^{-{3}/{2}})$ terms. Doing this gives

$$ \begin{align*} I&=\frac{\gamma^2\lambda^2}{4\pi^2}\bigg[\int_{\vert x\vert\leq\lambda^{-1}}a^2(\lambda^\alpha \vert x\vert)\mathcal{O}(1)\,dx\\&\quad+\int_{\lambda^{-1}\leq\vert x\vert}a^2(\lambda^\alpha \vert x\vert)\bigg(2\sqrt{2\pi}\lambda^{-{1}/{2}}\vert x\vert^{-{1}/{2}}\cos\bigg(\lambda\vert x\vert-\frac{\pi}{4}\bigg)+C\lambda^{-{3}/{2}}\vert x\vert^{-{3}/{2}}\bigg)^2\,dx\bigg]\\&=\frac{\gamma^2\lambda^2}{4\pi^2}\mathcal{O}\bigg(\int_{\vert x\vert\leq\lambda^{-1}}a^2(\lambda^\alpha \vert x\vert)\,dx\bigg)+\frac{\gamma^2\lambda^2}{4\pi^2}\int_{\lambda^{-1}\leq\vert x\vert}a^2(\lambda^\alpha \vert x\vert)8\pi\lambda^{-1}\vert x\vert^{-1}\cos^2\bigg(\lambda\vert x\vert-\frac{\pi}{4}\bigg)\,dx \\&\quad+\mathcal{O}(\gamma^2\int_{\lambda^{-1}\leq\vert x\vert}a^2(\lambda^\alpha \vert x\vert)\vert x\vert^{-2}\cos\bigg(\lambda\vert x\vert-\frac{\pi}{4}\bigg)\,dx\bigg). \end{align*} $$

Here the two error terms $\int C^2\lambda ^{-3}\vert x\vert ^{-3}\,dx$ and $\int C\lambda ^{-2}\vert x\vert ^{-2}\cos (\lambda \vert x\vert -{\pi }/{4})\,dx$ have been combined, so that we are only dealing with the leading error term.

In the region where $\vert x\vert \leq \lambda ^{-1}$ , the bump function $a^2(\lambda ^\alpha \vert x\vert )=1$ , so

$$ \begin{align*}\notag I&=\frac{\gamma^2\lambda^2}{4\pi^2}\mathcal{O}\bigg(\int_{\vert x\vert\leq\lambda^{-1}}1\,dx\bigg)+\frac{2\gamma^2\lambda}{\pi}\int_{\lambda^{-1}\leq\vert x\vert}a^2(\lambda^\alpha \vert x\vert)\vert x\vert^{-1}\cos^2\bigg(\lambda\vert x\vert-\frac{\pi}{4}\bigg)\,dx\\&\quad+\mathcal{O}\bigg(\gamma^2\int_{\lambda^{-1}\leq\vert x\vert}a^2(\lambda^\alpha \vert x\vert)\vert x\vert^{-2}\cos\bigg(\lambda\vert x\vert-\frac{\pi}{4}\bigg)\,dx\bigg). \end{align*} $$

Since the cut-off function is a radial function, as it is only a function of $\vert x\vert $ and not x, the second and third integrals can be converted into polar coordinates. We let $\vert x\vert =r$ and note that $dx=r\,dr\,d\theta $ , giving

$$ \begin{align*} I&=\mathcal{O}(\gamma^2)+\frac{2\gamma^2\lambda}{\pi}\int_0^{2\pi}\int_{\lambda^{-1}}a^2(\lambda^\alpha r)r^{-1}\cos^2\bigg(\lambda r-\frac{\pi}{4}\bigg)r\,dr\,d\theta\\[2pt]&\quad+\mathcal{O}\bigg(\gamma^2\int_0^{2\pi}\int_{\lambda^{-1}}^{\lambda^{-\alpha}}r^{-2}\cos\bigg(\lambda r-\frac{\pi}{4}\bigg)r\,dr\,d\theta\bigg)\notag\\&=\mathcal{O}(\gamma^2)+4\gamma^2\lambda\int_{\lambda^{-1}}a^2(\lambda^\alpha r)\cos^2\bigg(\lambda r-\frac{\pi}{4}\bigg)\,dr+\mathcal{O}\bigg(\gamma^2\int_{\lambda^{-1}}^{\lambda^{-\alpha}}\textstyle\frac{\cos\bigg(\lambda r-\dfrac{\pi}{4}\bigg)}{r}\,dr\bigg)\\[2pt]&=\mathcal{O}(\gamma^2)+2\gamma^2\lambda\int_{\lambda^{-1}}a^2(\lambda^\alpha r)(1+\sin(2\lambda r))\,dr+\mathcal{O}\bigg(\gamma^2\bigg[\frac{\text{Si}(\lambda r)+\text{Ci}(\lambda r)}{\sqrt2}\bigg]_{\lambda^{-1}}^{\lambda^{-\alpha}}\bigg)\\[3pt]&=\mathcal{O}(\gamma^2)+2\gamma^2\lambda\int_{\lambda^{-1}}a^2(\lambda^\alpha r)(1+\sin(2\lambda r))\,dr\\[3pt]&\quad+\mathcal{O}(\gamma^2[\text{Si}(\lambda^{1-\alpha})+\text{Ci}(\lambda^{1-\alpha})-\text{Si}(1)-\text{Ci}(1)]), \end{align*} $$

where $\text {Si}(z)$ is the sine integral defined as $\text {Si}(z)=\int _0^z{\sin t}/{t}\,dt$ and $\text {Ci}(z)$ is the cosine integral defined as $\text {Ci}(z)=-\int _{\pi }^{\infty }{\cos t}/{t}\,dt$ . Provided that $\lambda ^{1-\alpha }$ is large enough, which happens when $\lambda $ is large (that is, when $\gamma \to \infty $ ), the functions $\text {Si}(\lambda ^{1-\alpha })\to {\pi }/{2}$ and $\text {Ci}(\lambda ^{1-\alpha })\to 0$ do not grow, but tend to constants. As a result, the two error terms can be combined to give $\mathcal {O}(\gamma ^2)$ :

$$ \begin{align*}I=2\gamma^2\lambda\int_{\lambda^{-1}}a^2(\lambda^\alpha r)(1+\sin(2\lambda r))\,dr+\mathcal{O}(\gamma^2).\end{align*} $$

Due to the support and other properties of the cut-off function, and since the term being multiplied by the cut-off function was squared and is hence positive, we can form the following bounds:

(3-7) $$ \begin{align} 2\gamma^2\lambda\int_{\lambda^{-1}}^{\lambda^{-\alpha}}(1+\sin(2\lambda r))\,dr+\mathcal{O}(\gamma^2)\leq I \end{align} $$

and

(3-8) $$ \begin{align} I\leq2\gamma^2\lambda\int_{\lambda^{-1}}^{2\lambda^{-\alpha}}(1+\sin(2\lambda r))\,dr+\mathcal{O}(\gamma^2). \end{align} $$

Dealing with the lower bound (3-7) first,

$$ \begin{align*} 2\gamma^2\lambda\bigg[r-\frac{\cos(2\lambda r)}{2\lambda}\bigg]_{\lambda^{-1}}^{\lambda^{-\alpha}}+\mathcal{O}(\gamma^2)&\leq I,\\[3pt] 2\gamma^2\lambda\bigg[\lambda^{-\alpha}-\frac{\cos(2\lambda^{1-\alpha})}{2\lambda}-\lambda^{-1}+\frac{\cos(2)}{2\lambda}\bigg]+\mathcal{O}(\gamma^2)&\leq I,\\[3pt] 2\gamma^2\lambda^{1-\alpha}+\mathcal{O}(\gamma^2)&\leq I. \end{align*} $$

We can pick $\lambda $ to be large enough, so that $\lvert \mathcal {O}(\gamma ^2)\rvert \leq \gamma ^2\lambda ^{1-\alpha }$ . As a result we obtain the following bound:

$$ \begin{align*}\gamma^2\lambda^{1-\alpha}\leq I.\end{align*} $$

Dealing with the upper bound (3-8),

$$ \begin{align*} I&\leq2\gamma^2\lambda\bigg[r-\frac{\cos(2\lambda r)}{2\lambda}\bigg]_{\lambda^{-1}}^{2\lambda^{-\alpha}}+\mathcal{O}(\gamma^2),\\[-10pt] \\ I&\leq2\gamma^2\lambda\bigg[2\lambda^{-\alpha}-\frac{\cos(4\lambda^{1-\alpha})}{2\lambda}-\lambda^{-1}+\frac{\cos(2)}{2\lambda}\bigg]+\mathcal{O}(\gamma^2),\\ I&\leq4\gamma^2\lambda^{1-\alpha}+\mathcal{O}(\gamma^2). \end{align*} $$

We can pick $\lambda $ to be large enough, so that $\mathcal {O}(\gamma ^2)\leq \gamma ^2\lambda ^{1-\alpha }$ . As a result, we obtain the following bound:

$$ \begin{align*}I\leq5\gamma^2\lambda^{1-\alpha}.\end{align*} $$

Therefore, I is bounded by

(3-9) $$ \begin{align}\gamma^2\lambda^{1-\alpha}\leq I\leq5\gamma^2\lambda^{1-\alpha}.\end{align} $$

Recall that Lemma 3.2 gives us that

$$ \begin{align*}|\!|{a_{\lambda}E_{1}}|\!|_{L^{2}}\lesssim \gamma^{{1}/{2}}\lambda^{{1}/{2}-{\alpha}/{2}}\quad\text{and}\quad |\!|{a_{\lambda}E_{1}}|\!|_{L^{2}}\lesssim \gamma^{{1}/{2}}\lambda^{{1}/{2}-{\alpha}/{2}}.\end{align*} $$

Since, for fixed x, $I_{1}(x)$ and $I_{2}(x)$ enjoy the same upper bounds, the upper bound for I can be used to (upper) bound $|\!|{a_{\lambda }I_{1}}|\!|_{L^{2}}^{2}$ and $|\!|{a_{\lambda }I_{2}}|\!|_{L^{2}}^{2}$ . Therefore,

$$ \begin{align*} \vert S-I\vert&\leq |\!|{a_{\lambda}I_{1}}|\!|_{L^{2}}|\!|{a_\lambda E_{2}}|\!|_{L^{2}}+|\!|{a_\lambda I_{2}}|\!|_{L^{2}}|\!|{a_\lambda E_{1}}|\!|_{L^{2}}+|\!|{a_\lambda E_{1}}|\!|_{L^{2}}|\!|{a_\lambda E_{2}}|\!|_{L^{2}}\\ &\lesssim \gamma^{{3}/{2}}\lambda^{1-\alpha}+\gamma\lambda^{1-\alpha}.\end{align*} $$

Since we are only considering the case where $\gamma $ is large we can then sweep these errors into (3-9) to obtain $c,\ C$ so that

$$ \begin{align*}c\gamma^2\lambda^{1-\alpha}\leq S \leq C\gamma^2\lambda^{1-\alpha}.\end{align*} $$

We have now obtained both a lower bound and an upper bound for the sum S. Since this appears in the expression for the expectation (2-2), as

$$ \begin{align*}\mathbb{E}(\lVert a_\lambda u\rVert^2)=N\int{a^2(\lambda^\alpha \vert x\vert)\,dx}+(2p-1)^2S,\end{align*} $$

we can substitute the bounds for S to obtain an upper and lower bound for the expectation, in the case where $\gamma \to \infty $ . We also use the property of the cut-off function to obtain the required bounds for the first integral, which comes from the diagonal terms. This gives the following bounds for the expectation:

(3-10) $$ \begin{align} \pi\gamma\lambda^{1-2\alpha}+c(2p-1)^2\gamma^2\lambda^{1-\alpha}<\mathbb{E}(\lVert a_\lambda u\rVert^2)<4\pi\gamma\lambda^{1-2\alpha}+C(2p-1)^2\gamma^2\lambda^{1-\alpha}. \end{align} $$

Equidistribution. Equation (3-10) gives the bounds on the expectation in the case where $\gamma \to \infty $ . After normalisation, the second term in them is on the scale of $\gamma \lambda ^{-\alpha }$ . Therefore, the weak property of equidistribution, (1-4), holds when

$$ \begin{align*} (2p-1)^2\gamma\lambda^{-\alpha}&=\mathcal{O}(\lambda^{-2\alpha}),\\ (2p-1)^2&=\mathcal{O}(\lambda^{-\alpha}\gamma^{-1}),\\ p&=0.5+\mathcal{O}(\lambda^{-{\alpha}/{2}}\gamma^{-{1}/{2}}). \end{align*} $$

Therefore, up to constants, if the probability is $\lambda ^{-{\alpha }/{2}}\gamma ^{-{1}/{2}}$ close to 0.5, the expectation will scale with the volume of the region, and the weak equidistribution property holds. This is summarised by the following corollary.

Corollary 3.4. A random wave given by (1-1) where the coefficients are determined by an unfair coin ( $C_j=+1$ has probability p and $C_j=-1$ has probability $1-p$ ), and where $\gamma \to \infty $ , satisfies the condition on the expectation for the weak property of equidistribution, given by (1-4), if

$$ \begin{align*}\lvert p-0.5\rvert\lesssim\lambda^{-{\alpha}/{2}}\gamma^{-{1}/{2}}.\end{align*} $$

4 Proof of Theorem 1.3

The variance of a quantity is given by

$$ \begin{align*}\sigma^2(\lVert a_\lambda u\rVert^2)=\mathbb{E}((\lVert a_\lambda u\rVert^2-\mathbb{E}(\lVert a_\lambda u\rVert^2))^2).\end{align*} $$

We can use the independence of the coefficients $C_j$ to obtain an expression for the variance in terms of the same off-diagonal terms involving oscillatory integrals, which were considered in the expectation. To simplify the expressions, we define

$$ \begin{align*}I_{jl}=\int{a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}.\end{align*} $$

In the case where $j=l$ we have $I_{jl}=\int {a^2(\lambda ^\alpha \vert x\vert )\,dx}$ . It also follows that $\vert I_{jl}\vert =\vert I_{lj}\vert $ .

Proposition 4.1. The variance of $\lVert a_\lambda u\rVert ^2$ for a random wave $u(x)$ given by (1-1), where the coefficients are determined by an unfair coin ( $C_j=+1$ has probability p and $C_j=-1$ has probability $1-p$ ), can be expressed as

$$ \begin{align*}\notag \sigma^2(\lVert a_\lambda u\rVert^2)&=[1-(2p-1)^2]^2\bigg[\sum_{\substack{j,l\\j\neq l}}I_{jl}^2+\sum_{\substack{j,l\\j\neq l}}I_{jl}I_{lj}\bigg]\\&\quad+[(2p-1)^2-(2p-1)^4]\cdot\bigg[\sum_j\bigg(\sum_{l\neq j}I_{jl}\bigg)\bigg(\sum_{n\neq j}I_{jn}\bigg)\\&\quad+\sum_j\bigg(\sum_{l\neq j}I_{jl}\bigg)\bigg(\sum_{m\neq j}I_{mj}\bigg)+\sum_l\bigg(\sum_{j\neq l}I_{jl}\bigg)\bigg(\sum_{n\neq l}I_{ln}\bigg) \\ &\quad +\sum_l\bigg(\sum_{j\neq l}I_{jl}\bigg)\bigg(\sum_{m\neq l}I_{ml}\bigg)\bigg]. \end{align*} $$

Proof. We begin by substituting the formula for the random wave into the expression for the variance:

(4-1) $$ \begin{align}\notag \sigma^2(\lVert a_\lambda u\rVert^2)&=\sum_kP_k\bigg[\iint\sum_{j,l,m,n}a^2(\lambda^\alpha \vert x\vert)a^2(\lambda^\alpha \vert y\vert)C^{(k)}_jC^{(k)}_lC^{(k)}_mC^{(k)}_n\\&\quad\times e^{i\lambda x\cdot(\xi_j-\xi_l)}e^{i\lambda y\cdot(\xi_m-\xi_n)}\,dx\,dy -\mathbb{E}(\lVert a_\lambda u\rVert^2)^2\bigg]\notag\\ &=\sum_kP_k\bigg[\sum_{j,l,m,n}C^{(k)}_jC^{(k)}_lC^{(k)}_mC^{(k)}_nI_{jl}I_{mn}-\mathbb{E}(\lVert a_\lambda u\rVert^2)^2\bigg]. \end{align} $$

From (2-2) we have an expression for the expectation in terms of the integrals in the diagonal and off-diagonal terms:

$$ \begin{align*} \mathbb{E}(\lVert a_\lambda u\rVert^2)&=N\int{a^2(\lambda^\alpha \vert x\vert)\,dx}+(2p-1)^2\sum_{\substack{j,l\\j\neq l}}\int{a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\\&=N\int{a^2(\lambda^\alpha \vert x\vert)\,dx}+(2p-1)^2\sum_{\substack{j,l\\j\neq l}}I_{jl}, \end{align*} $$

which can be substituted into the expression for the variance to achieve some cancellation. To see the cancellation we need to compute $\mathbb {E}^2$ :

(4-2) $$ \begin{align} \mathbb{E}(\lVert a_\lambda u\rVert^2)^2&=N^2\iint{a^2(\lambda^\alpha \vert x\vert)a^2(\lambda^\alpha \vert y\vert)\,dx\,dy}\nonumber\\&\quad+2N\int{a^2(\lambda^\alpha \vert y\vert)\,dy}\cdot(2p-1)^2\sum_{\substack{j,l\\j\neq l}}I_{jl}+(2p-1)^4\cdot\sum_{\substack{j,l\\j\neq l}}I_{jl}\cdot\sum_{\substack{m,n\\m\neq n}}I_{mn}\nonumber\\&=N^2\iint{a^2(\lambda^\alpha \vert x\vert)a^2(\lambda^\alpha \vert y\vert)\,dx\,dy}\nonumber\\&\quad+2N(2p-1)^2\sum_{\substack{j,l\\j\neq l}}I_{jl}\int{a^2(\lambda^\alpha \vert y\vert)\,dy}+(2p-1)^4\sum_{\substack{j,l,m,n\\j\neq l\\m\neq n}}I_{jl}I_{mn}. \end{align} $$

This expression can be taken outside of the sum over k since it does not depend on k, and the resulting sum $\sum _kP_k$ equals 1. The first term in the expression for the variance, (4-1),

$$ \begin{align*}\sum_kP_k\bigg(\sum_{j,l,m,n}C^{(k)}_jC^{(k)}_lC^{(k)}_mC^{(k)}_nI_{jl}I_{mn}\bigg),\end{align*} $$

needs to be split into different combinations of j, l, m and n for cancellation with terms in the expression for $\mathbb {E}^2$ , (4-2). Important terms are those in which there are pairs of j, l, m or n that are equal, since in those cases the coefficients are not dependent on probabilities and in some cases where $j=l$ or $m=n$ the exponents simplify:

Case 1: $j=l$ and $m=n$ .

$$ \begin{align*} \sum_kP_k\sum_{j,m}\iint{a^2(\lambda^\alpha \vert x\vert)a^2(\lambda^\alpha \vert y\vert)(C^{(k)}_j)^2(C^{(k)}_m)^2\,dx\,dy}=N^2\iint{a^2(\lambda^\alpha \vert x\vert)a^2(\lambda^\alpha \vert y\vert)\,dx\,dy}.\end{align*} $$

This cancels out with the first term in (4-2).

Case 2: $j=l$ but $m\neq n$ .

$$ \begin{align*}\notag \sum_kP_k\sum_{\substack{j,m,n\\m\neq n}}(C^{(k)}_j)^2C^{(k)}_mC^{(k)}_nI_{mn}\int{a^2(\lambda^\alpha \vert x\vert)\,dx}=N\sum_{\substack{m,n\\m\neq n}}\sum_kP_kC^{(k)}_mC^{(k)}_nI_{mn}\int{a^2(\lambda^\alpha \vert x\vert)\,dx}. \end{align*} $$

From Lemma 2.1, we know that $\sum _kP_kC^{(k)}_mC^{(k)}_n=(2p-1)^2$ , and hence,

$$ \begin{align*}\notag \sum_kP_k\sum_{\substack{j,m,n\\m\neq n}}(C^{(k)}_m)^2C^{(k)}_mC^{(k)}_nI_{mn}\int{a^2(\lambda^\alpha \vert x\vert)\,dx}=N(2p-1)^2\sum_{\substack{m,n\\m\neq n}}I_{mn}\int a^2(\lambda^\alpha \vert x\vert)\,dx. \end{align*} $$

Case 3: $j\neq l$ but $m=n$ . This case is similar to the $j=l$ but $m\neq n$ case, and so

$$ \begin{align*}\notag \sum_kP_k\sum_{\substack{j,l,m\\j\neq l}}(C^{(k)}_j)^2C^{(k)}_jC^{(k)}_l I_{jl}\int{a^2(\lambda^\alpha \vert y\vert)\,dy}=N(2p-1)^2\sum_{\substack{j,l\\j\neq l}}I_{jl}\int a^2(\lambda^\alpha \vert y\vert)\,dy. \end{align*} $$

Since the indices are arbitrary, these two cases (Cases 2 and 3) cancel out the second term in the expression for $\mathbb {E}^2$ , (4-2). This leaves

(4-3) $$ \begin{align}\notag \sigma^2(\lVert a_\lambda u\rVert^2)&=\sum_kP_k\sum_{\substack{j,l,m,n\\j\neq l\\m\neq n}}C^{(k)}_jC^{(k)}_lC^{(k)}_mC^{(k)}_nI_{jl}I_{mn}-(2p-1)^4\sum_{\substack{j,l,m,n\\j\neq l\\m\neq n}}I_{jl}I_{mn}\\ &=\bigg[\sum_kP_kC^{(k)}_jC^{(k)}_lC^{(k)}_mC^{(k)}_n-(2p-1)^4\bigg]\sum_{\substack{j,l,m,n\\j\neq l\\m\neq n}}I_{jl}I_{mn}. \end{align} $$

For the terms where $j, l, m$ and n are independent, $\sum _kP_kC^{(k)}_jC^{(k)}_l C^{(k)}_m C^{(k)}_n$ needs to be evaluated in terms of p. In this calculation we fix j, l, m and n. Since the values of the entries of interest (j, l, m and n) are independent of each other, the probabilities of the different combinations of coefficients can be calculated by a similar argument to Lemma 2.1 as follows:

$$ \begin{align*} \sum_kP_kC^{(k)}_jC^{(k)}_lC^{(k)}_mC^{(k)}_n&=\mathbb{E}(C_j^{(k)}C_l^{(k)}C^{(k)}_mC^{(k)}_n)\\&=\mathbb{E}(C_j^{(k)})\cdot\mathbb{E}(C_l^{(k)})\cdot\mathbb{E}(C_m^{(k)})\cdot\mathbb{E}(C_n^{(k)})=(2p-1)^4.\end{align*} $$

This is the same coefficient as that of the second term in (4-3), so all these terms will cancel. The remaining cases are the terms where $(\kern1.5pt j,l,m,n)$ are not all distinct but $j\neq l$ and $m\neq n$ . These include the other pair terms, ( $\kern1.5pt j=m$ , $l=n$ ) and ( $\kern1.5pt j=n$ , $l=m$ ), as well as the four cases where there is only one pair.

Case 4: $j=m$ and $l=n (m\neq l)$ . This contributes a term of the form

$$ \begin{align*} [1-(2p-1)^4]\sum_{\substack{j,l\\j\neq l}}I_{jl}^2. \end{align*} $$

Case 5: $j=n$ and $l=m (n\neq l)$ . This contributes a term of the form

$$ \begin{align*} [1-(2p-1)^4]\sum_{\substack{j,l\\j\neq l}}I_{jl}I_{lj}. \end{align*} $$

Case 6: $j=m$ and $l\neq n\neq j$ . This contributes the following terms:

$$ \begin{align*} &\bigg[\sum_kP_kC^{(k)}_lC^{(k)}_n-(2p-1)^4\bigg]\sum_{\substack{j,l,n\\j\neq l, j\neq n\\l\neq n}}I_{jl}I_{jn}\\&\quad=[(2p-1)^2-(2p-1)^4]\bigg[\sum_j\bigg(\sum_{l\neq j}I_{jl}\bigg)\bigg(\sum_{n\neq j}I_{jn}\bigg)-\sum_{\substack{j,l\\j\neq l}}I_{jl}^2\bigg] \end{align*} $$

as by Lemma 2.1 we know that $\sum _kP_kC^{(k)}_mC^{(k)}_n=(2p-1)^2$ . The term $\sum _{j,l,\ j\neq l}I_{j,l}^2$ corresponds to subtracting the terms corresponding to $l=n$ .

Case 7: $j=n$ and $l\neq m\neq j$ , Case 8: $l=m$ and $j\neq n\neq l$ and Case 9: $l=n$ and ${j\neq m\neq l}$ . These are similar to Case 6 and contribute the following, where we manually remove the terms where $l=m$ , $j=n$ and $j=m$ for each case, respectively:

$$ \begin{align*}\notag &[(2p-1)^2-(2p-1)^4]\bigg[\sum_j\bigg(\sum_{l\neq j}I_{jl}\bigg)\bigg(\sum_{m\neq j}I_{mj}\bigg)-\sum_{\substack{j,l\\j\neq l}}I_{jl}I_{lj}\bigg]\\ &\quad+[(2p-1)^2-(2p-1)^4]\bigg[\sum_l\bigg(\sum_{j\neq l}I_{jl}\bigg)\bigg(\sum_{n\neq l}I_{ln}\bigg)-\sum_{\substack{j,l\\j\neq l}}I_{jl}I_{lj}\bigg]\\ &\quad+[(2p-1)^2-(2p-1)^4]\bigg[\sum_l\bigg(\sum_{j\neq l}I_{jl}\bigg)\bigg(\sum_{m\neq l}I_{ml}\bigg)-\sum_{\substack{j,l\\j\neq l}}I_{jl}^2\bigg]. \end{align*} $$

Combining all these terms gives the following expression for the variance:

$$ \begin{align*}\notag \sigma^2(\lVert a_\lambda u\rVert^2)&=[1-(2p-1)^4]\bigg[\sum_{\substack{j,l\\j\neq l}}I_{jl}^2+\sum_{\substack{j,l\\j\neq l}}I_{jl}I_{lj}\bigg]\\&\quad+[(2p-1)^2-(2p-1)^4]\cdot\bigg[\sum_j\bigg(\sum_{l\neq j}I_{jl}\bigg)\bigg(\sum_{n\neq j}I_{jn}\bigg)\\&\quad+\sum_j\bigg(\sum_{l\neq j}I_{jl}\bigg)\bigg(\sum_{m\neq j}I_{mj}\bigg)+\sum_l\bigg(\sum_{j\neq l}I_{jl}\bigg)\bigg(\sum_{n\neq l}I_{ln}\bigg)\\&\quad+\sum_l\bigg(\sum_{j\neq l}I_{jl}\bigg)\bigg(\sum_{m\neq l}I_{ml}\bigg)-2\bigg(\sum_{\substack{j,l\\j\neq l}}I_{jl}^2+\sum_{\substack{j,l\\j\neq l}}I_{jl}I_{lj}\bigg)\bigg]. \end{align*} $$

These terms can be regrouped as follows:

$$ \begin{align*}\notag \sigma^2(\lVert a_\lambda u\rVert^2)&=[1-2(2p-1)^2+(2p-1)^4]\bigg[\sum_{\substack{j,l\\j\neq l}}I_{jl}^2+\sum_{\substack{j,l\\j\neq l}}I_{jl}I_{lj}\bigg]\\&\quad+[(2p-1)^2-(2p-1)^4]\cdot\bigg[\sum_j\bigg(\sum_{l\neq j}I_{jl}\bigg)\bigg(\sum_{n\neq j}I_{jn}\bigg)\\&\quad+\sum_j\bigg(\sum_{l\neq j}I_{jl}\bigg)\bigg(\sum_{m\neq j}I_{mj}\bigg)+\sum_l\bigg(\sum_{j\neq l}I_{jl}\bigg)\bigg(\sum_{n\neq l}I_{ln}\bigg)+\sum_l\bigg(\sum_{j\neq l}I_{jl}\bigg)\bigg(\sum_{m\neq l}I_{ml}\bigg)\bigg]. \end{align*} $$

This concludes the proof.

From here we can continue the proof of Theorem 1.3, by computing an upper bound for the integrals in the above expression, using methods from Section 2.

Upper bound. We can recognise the square

$$ \begin{align*}(1-(2p-1)^2)^2=1-2(2p-1)^2+(2p-1)^4\end{align*} $$

from the statement of Proposition 4.1, and, using the triangle inequality over the different terms as well as the finite sums, we get

$$ \begin{align*}\notag \vert\sigma^2(\lVert a_\lambda u\rVert^2)\vert&\leq[1-(2p-1)^2]^2\bigg[\sum_{\substack{j,l\\j\neq l}}\vert I_{jl}\vert^2+\sum_{\substack{j,l\\j\neq l}}\vert I_{jl}\vert\vert I_{lj}\vert\bigg]\\&\quad+[(2p-1)^2-(2p-1)^4]\cdot\bigg[\sum_j\bigg(\sum_{l\neq j}\vert I_{jl}\vert\bigg)\bigg(\sum_{n\neq j}\vert I_{jn}\vert\bigg)\\&\quad+\sum_j\bigg(\sum_{l\neq j}\vert I_{jl}\vert\bigg)\bigg(\sum_{m\neq j}\vert I_{mj}\vert\bigg)+\sum_l\bigg(\sum_{j\neq l}\vert I_{jl}\vert\bigg)\bigg(\sum_{n\neq l}\vert I_{ln}\vert\bigg)\\&\quad+\sum_l\bigg(\sum_{j\neq l}\vert I_{jl}\vert\bigg)\bigg(\sum_{m\neq l}\vert I_{ml}\vert\bigg)\bigg]. \end{align*} $$

The absolute values allow us to group the cases together, using $\vert I_{jl}\vert =\vert I_{lj}\vert $ , and substituting in for $I_{jl}$ gives

$$ \begin{align*}\notag \sigma^2&\leq2[1-(2p-1)^2]^2\bigg[\sum_{\substack{j,l\\j\neq l}}\bigg\lvert\int{a^2(\lambda^\alpha \vert x\vert)e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx}\bigg\rvert^2\bigg]\\ &\quad+4[(2p-1)^2-(2p-1)^4]\cdot\bigg[\sum_j\bigg(\sum_{l\neq j}\bigg\vert\int a^2(\lambda^\alpha \vert x\vert) e^{i\lambda x\cdot(\xi_j-\xi_l)}\,dx\bigg\vert\bigg)^2\bigg]. \end{align*} $$

We now use the same upper bound (2-7) for the integrals in this expression, which was obtained as a result of Theorem 2.2 in the calculation for the expectation:

$$ \begin{align*}\notag \sigma^2(\lVert a_\lambda u\rVert^2)&\lesssim 2[1-(2p-1)^2]^2\bigg[\sum_{\substack{j,l\\j\neq l}}\bigg(\lambda^{-2\alpha}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-n}\bigg)^2\bigg]\\ &\quad+4[(2p-1)^2-(2p-1)^4]\cdot\bigg[\sum_j\bigg(\sum_{l\neq j}\bigg(\lambda^{-2\alpha}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-n}\bigg)\bigg)^2\bigg], \end{align*} $$

$$ \begin{align*}\notag \sigma^2(\lVert a_\lambda u\rVert^2)&\lesssim2[1-(2p-1)^2]^2\lambda^{-4\alpha}\sum_j\bigg[\sum_{\substack{l\\l\neq j}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-2n}\bigg]\\ &\quad+4[(2p-1)^2-(2p-1)^4]\lambda^{-4\alpha}\sum_j\bigg[\sum_{\substack{l\\l\neq j}}\bigg(1+\frac{\vert\xi_j-\xi_l\vert}{\lambda^{-1+\alpha}}\bigg)^{-n}\bigg]^2. \end{align*} $$

We can use Lemma 2.3, which evaluates the sum over l using a dyadic decomposition, to rewrite this as

$$ \begin{align*} \sigma^2(\lVert a_\lambda u\rVert^2)&\lesssim2[1-(2p-1)^2]^2\lambda^{-4\alpha}\sum_j[ \gamma\lambda^\alpha]\\ &\quad+4[(2p-1)^2-(2p-1)^4]\lambda^{-4\alpha}\sum_j[ \gamma\lambda^\alpha]^2, \end{align*} $$

where the implicit constant is determined by the number of integrations by parts necessary to estimate the inner sum (in this case at least two iterations are necessary). Since this is independent of j, the sum over j is evaluated by multiplying by $N=\gamma \lambda $ . Simplifying this then gives the desired upper bound:

(4-4) $$ \begin{align} \sigma^2(\lVert a_\lambda u\rVert^2)&\lesssim2[1-(2p-1)^2]^2\lambda^{-4\alpha}\cdot\lambda\gamma\cdot\gamma\lambda^\alpha \nonumber\\&\quad+4[(2p-1)^2-(2p-1)^4]\lambda^{-4\alpha}\cdot\lambda\gamma\cdot\gamma^2\lambda^{2\alpha}\nonumber\\[6pt]&\lesssim[1-(2p-1)^2]^2\gamma^2\lambda^{1-3\alpha}+(2p-1)^2[1-(2p-1)^2]\gamma^3\lambda^{1-2\alpha}. \end{align} $$

Equidistribution. Equation (4-4) gives the upper bound on the variance in the case where $\gamma \to \infty $ . After normalisation, dividing by $N^2=\gamma ^2\lambda ^2$ , this becomes

$$ \begin{align*}\sigma^2\lesssim\lambda^{-1-3\alpha}[1-(2p-1)^2]^{2}+\gamma\lambda^{-1-2\alpha}(2p-1)^2[1-(2p-1)^2].\end{align*} $$

If we assume the condition given by Corollary 3.4, that is,

$$ \begin{align*}(2p-1)^2=\mathcal{O}(\lambda^{-\alpha}\gamma^{-1}),\end{align*} $$

then the second term is of the same size as the first:

$$ \begin{align*}\sigma^2\lesssim\lambda^{-1-3\alpha}[1-(2p-1)^2]^2+\lambda^{-1-3\alpha}[1-(2p-1)^2].\end{align*} $$

Therefore, the requirement on the variance for equidistribution, equation (1-3), holds when $\alpha <1$ and $(2p-1)^2=\mathcal {O}(\lambda ^{-\alpha }\gamma ^{-1})$ . This is summarised by the following corollary.

Corollary 4.2. A random wave given by (1-1) where the coefficients are determined by an unfair coin ( $C_j=+1$ has probability p and $C_j=-1$ has probability $1-p$ ), and where $\gamma \to \infty $ , satisfies the condition for equidistribution on the variance, given by (1-3), and hence the weak equidistribution property given by (1-4), if $\lvert p-0.5\rvert \lesssim \lambda ^{-{\alpha }/{2}}\gamma ^{-{1}/{2}}$ and $\alpha <1$ .