SOLENOIDAL MAPS, AUTOMATIC SEQUENCES, VAN DER PUT SERIES, AND MEALY AUTOMATA

Abstract

The ring 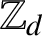$\mathbb Z_{d}$ of d-adic integers has a natural interpretation as the boundary of a rooted d-ary tree 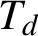$T_{d}$ . Endomorphisms of this tree (that is, solenoidal maps) are in one-to-one correspondence with 1-Lipschitz mappings from 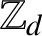$\mathbb Z_{d}$ to itself. In the case when 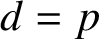$d=p$ is prime, Anashin [‘Automata finiteness criterion in terms of van der Put series of automata functions’,p-Adic Numbers Ultrametric Anal. Appl. 4(2) (2012), 151–160] showed that 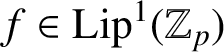$f\in \mathrm {Lip}^{1}(\mathbb Z_{p})$ is defined by a finite Mealy automaton if and only if the reduced coefficients of its van der Put series constitute a p-automatic sequence over a finite subset of 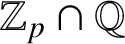$\mathbb Z_{p}\cap \mathbb Q$ . We generalize this result to arbitrary integers 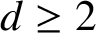$d\geq 2$ and describe the explicit connection between the Moore automaton producing such a sequence and the Mealy automaton inducing the corresponding endomorphism of a rooted tree. We also produce two algorithms converting one automaton to the other and vice versa. As a demonstration, we apply our algorithms to the Thue–Morse sequence and to one of the generators of the lamplighter group acting on the binary rooted tree.

1 Introduction

Continuous self-maps of the ring $\mathbb Z_{p}$ of p-adic integers are the objects of study of p-adic analysis and p-adic dynamics. Among all continuous functions $\mathbb Z_{p}\to \mathbb Z_{p}$ , there is an natural subclass of $1$ -Lipschitz functions that do not increase the distances between points of $\mathbb Z_{p}$ . These functions appear in many contexts and have various names in the literature. For example, Bernstein and Lagarias in the paper devoted to the Collatz ‘ $3n+1$ ’ conjecture call them solenoidal maps [10], Anashin in [3] (see also [5]) studied the conditions under which these functions act ergodically on $\mathbb Z_{p}$ . For us, such functions are especially important because they act on regular rooted trees by endomorphisms (or automorphisms in the invertible case). Topologically, $\mathbb Z_{p}$ is homeomorphic to the Cantor set which, in turn, can be identified with the boundary $X^{\infty }$ of a rooted p-ary tree $X^{*}$ , whose vertices are finite words over the alphabet $X=\{0,1,\ldots ,p-1\}$ . Namely, we identify a p-adic number $x_{0}+x_{1}p+x_{2}p^{2}+\cdots $ with the point $x_{0}x_{1}x_{2}\ldots \in X^{\infty }$ . (For the language of rooted trees and group actions on them, see [17, 23].)

Under this identification Nekrashevych, Sushchansky, and the first author [23, Proposition 3.7] showed that a continuous map from $\mathbb Z_{p}$ to itself induces a (graph) endomorphism of the tree $X^{*}$ precisely when it is 1-Lipschitz. Furthermore, it is an easy but not so well-known observation that the group $\mathop {\mathrm {Isom}}\nolimits (\mathbb Z_{p})$ of isometries of $\mathbb Z_{p}$ is naturally isomorphic to the group $\mathop {\mathrm {Aut}}\nolimits (X^{*})$ of automorphisms of a rooted p-ary tree. As such, the groups $\mathop {\mathrm {Isom}}\nolimits (\mathbb Z_{p})$ contain many exotic groups that provide counterexamples to several long standing conjectures and problems in group theory [20–22, 25] and have connections to other areas of mathematics, such as holomorphic dynamics [8, 33], combinatorics [19], analysis on graphs [18], computer science [11, 29, 30], cryptography [13, 31, 32, 35], and coding theory [12, 19]. In a similar way, one can characterize the group $\mathop {\mathrm {Isom}}\nolimits (\mathbb Q_{p})$ of isometries of the field $\mathbb Q_{p}$ of p-adic numbers as the group of automorphisms of a regular (not rooted) $(p+1)$ -ary tree that fix the pointwise one selected end of this tree.

To describe important subgroups of $\mathop {\mathrm {Isom}}\nolimits (\mathbb Z_{p})$ and establish their properties, the languages of self-similar groups and semigroups initiated in [20] and developed in the last four decades (see survey papers [6, 23] and the book [33]), and Mealy automata have proved to be very effective. However, these tools were not widely used by researchers studying p-adic analysis and p-adic dynamics. There are only a few papers that build bridges between the two worlds. The first realization of an affine transformation of $\mathbb Z_{p}$ by a finite Mealy automaton was constructed by Bartholdi and Šuniḱ in [9]. Ahmed and the second author in [1] described automata defining polynomial functions $x\mapsto f(x)$ on $\mathbb Z_{d}$ , where $f\in \mathbb Z[x]$ , and using the language of groups acting on rooted trees, deduced conditions for ergodicity of the action of f on $\mathbb Z_{2}$ obtained by completely different methods by Larin [27]. In [4], Anashin proved an excellent result relating finiteness of the Mealy automaton generating an endomorphism of the p-ary tree to automaticity of the sequence of reduced van der Put coefficients of the induced functions on $\mathbb Z_{p}$ , which are discussed below in detail. Automatic sequences represent an important area at the conjunction of computer science and mathematics. Some of the famous examples of automatic sequences include the Thue–Morse sequence and Rudin–Shapiro sequence defining space filling curves. We refer the reader to [2] for details. Recent applications of automatic sequences in group theory include [15, 16].

As in the real analysis, one of the effective ways to study functions $\mathbb Z_{p}\to \mathbb Z_{p}$ is to decompose them into series with respect to some natural basis in the space of continuous functions $C(\mathbb Z_{p})$ from $\mathbb Z_{p}$ to itself. Two of the most widely used bases of this space are the Mahler basis and the van der Put basis [28, 36]. In the more general settings of the spaces of continuous functions from $\mathbb Z_{p}$ to a field, several other bases have been used in the literature: Walsh basis [38]; Haar basis (used in group theory context, for example, in [7]); Kaloujnine basis [16]. In this paper, we deal with the van der Put basis, which is made of functions $\chi _{n}(x)$ , $n\geq 0$ that are characteristic functions of cylindrical subsets of $\mathbb Z_{p}$ consisting of all elements that have the p-adic expansion of n as a prefix. Each continuous function $f\in C(\mathbb Z_{p})$ can be decomposed uniquely as

$$ \begin{align*} f(x)=\sum_{n\geq 0}B^{f}_{n}\chi_{n}(x), \end{align*} $$

where the coefficients $B^{f}_{n}$ are elements of $\mathbb Z_{p}$ which we call van der Put coefficients. A function $f\colon \mathbb Z_{p}\to \mathbb Z_{p}$ is 1-Lipschitz if and only if its van der Put coefficients can be represented as $B^{f}_{n}=b^{f}_{n}d^{\lfloor \log _{d}n\rfloor }$ for all $n>0$ , where $b^{f}_{n}\in \mathbb Z_{p}$ [5]. We call $b^{f}_{n}$ the reduced van der Put coefficients (see Section 3 for details).

The main results of the present paper are the following two theorems, in which $d\geq 2$ is an arbitrary (not necessarily prime) integer.

Theorem 1.1. Let $g\in \mathop {\mathrm {End}}\nolimits (X^{*})$ be an endomorphism of the rooted tree $X^{*}$ , where $X=\{0,1,\ldots ,d-1\}$ . Then g is finite state if and only if the following two conditions hold for the transformation $\hat g$ of $\mathbb Z_{d}$ induced by g:

1. (a) the sequence $(b_{n}^{\hat g})_{n\geq 1}$ of reduced van der Put coefficients of $\hat g$ consists of finitely many eventually periodic elements from $\mathbb Z_{d}$ ;

2. (b) $(b_{n}^{\hat g})_{n\geq 1}$ is d-automatic.

For the case of prime $d=p$ , Theorem 1.1 was proved by Anashin in [4] using a completely different method from our approach. The proof from [4] does not provide a direct connection between the Mealy automaton of an endomorphism of $X^{*}$ and the Moore automaton of the corresponding sequence of its reduced van der Put coefficients. Our considerations are based on understanding the connection between the reduced van der Put coefficients of an endomorphism and of its sections at vertices of the rooted tree via the geometric notion of a portrait. This connection, summarized in the next theorem, bears a distinct geometric flavor and provides a way to effectively relate the corresponding Mealy and Moore automata.

Theorem 1.2. Let $X=\{0,1,\ldots ,d-1\}$ be a finite alphabet identified with $\mathbb Z/d\mathbb Z$ .

1. (a) Given an endomorphism g of the tree $X^{*}$ , defined by the finite Mealy automaton, there is an explicit algorithmic procedure given by Theorem 7.1 and Algorithm 7.3 that constructs the finite Moore automaton generating the sequence $(b_{n}^{g})_{n\geq 0}$ of reduced van der Put coefficients of g.

2. (b) Conversely, given a finite Moore automaton generating the sequence $(c_{n})_{n\geq 0}$ of eventually periodic d-adic integers, there is an explicit algorithmic procedure given by Theorem 7.7 and Algorithm 7.8 that constructs the finite Mealy automaton of an endomorphism g whose reduced van der Put coefficients satisfy $b_{n}^{g}=c_{n}$ for all $n\geq 0$ .

3. (c) Both constructions are dual to each other in a sense that the automata produced by them cover the input automata as labeled graphs (see Section 7 for the exact definition).

Theorem 1.2 opens up a new approach to study automatic sequences by means of (semi)groups acting on rooted trees, and vice versa, to study endomorphisms of rooted trees via the language of Moore automata. Note that in this context, unlike in the p-adic analysis, the fact that the size of the alphabet can be chosen to be not necessarily prime plays an important role since there are important automatic sequences over such alphabets, as well as interesting endomorphisms of d-regular rooted trees, where d is not a prime number.

In [4], Anashin, using Christol’s famous characterization of p-automatic sequences in terms of algebraicity of the corresponding power series, suggested another version of the main result of his paper (that is, of Theorem 1.1 in the case of prime d). The authors are not aware of the existence of an analog of Christol’s theorem in the situation of d-automaticity when d is not prime. The first question that arises is how to define the algebraicity of a function when the field $\mathbb Q_{p}$ is replaced by the ring $\mathbb Q_{d}$ of d-adic numbers. The authors do not exclude that the extension of Christol’s theorem is possible and leave this question for the future.

The paper is organized as follows. Section 2 introduces necessary notions related to Mealy automata and actions on rooted trees. Section 3 recalls how to represent a continuous function $\mathbb Z_{d}\to \mathbb Z_{d}$ by a van der Put series. We consider automatic sequences and define their portraits and sections in Section 4. The crucial argument relating van der Put coefficients of endomorphisms and their sections is given in Section 5. Section 6 contains the proof of Theorem 1.1. The algorithms relating Mealy and Moore automata associated with an endomorphism of $X^{*}$ and constituting the proof of Theorem 1.2, are given in Section 7. Finally, two examples are worked out in full detail in Section 8 to conclude the paper.

2 Mealy automata and endomorphisms of rooted trees

We start this section by introducing the notions and terminology of endomorphisms and automorphisms of regular rooted trees and transformations generated by Mealy automata. For more details, the reader is referred to [23].

Let $X=\{0,1,\ldots ,d-1\}$ be a finite alphabet with $d\geq 2$ elements (called letters) and let $X^{*}$ denote the set of all finite words over X. The set $X^{*}$ can be equipped with the structure of a rooted d-ary tree by declaring that v is adjacent to $vx$ for every $v\in X^{*}$ and $x\in X$ . Thus finite words over X serve as vertices of the tree. The empty word corresponds to the root of the tree and for each positive integer n, the set $X^{n}$ corresponds to the n th level of the tree. Also, the set $X^{\infty }$ of infinite words over X can be identified with the boundary of the tree $X^{*}$ , which consists of all infinite paths in the tree, without backtracking, initiating at the root. We consider endomorphisms and automorphisms of the tree $X^{*}$ (that is, the maps and bijections of $X^{*}$ that preserve the root and the adjacency of vertices). We sometimes denote the tree $X^{*}$ as $T_{d}$ . The semigroup of all endomorphisms of $T_{d}$ is denoted by $\mathop {\mathrm {End}}\nolimits (T_{d})$ and the group of all automorphisms of $T_{d}$ is denoted by $\mathop {\mathrm {Aut}}\nolimits (T_{d})$ . To operate with such objects, we use the language of Mealy automata.

Definition 2.1. A Mealy automaton (or simply automaton) is a 4-tuple

$$ \begin{align*}(Q,X,\delta,\lambda),\end{align*} $$

where

• • Q is a set of states;

• • X is a finite alphabet (not necessarily $\{0,1,\ldots ,d-1\}$ );

• • $\delta \colon Q\times X\to Q$ is the transition function;

• • $\lambda \colon Q\times X\to X$ is the output function.

If the set of states Q is finite, the automaton is called finite. If for every state $q\in Q$ the output function $\lambda _{q}(x)=\lambda (q,x)$ induces a permutation of X, the automaton $\mathcal A$ is called invertible. Selecting a state $q\in Q$ produces an initial automaton $\mathcal A_{q}$ , which formally is a $5$ -tuple $(Q,X,\delta ,\lambda ,q)$ .

Here we consider automata with the same input and output alphabets.

Automata are often represented by their Moore diagrams. The Moore diagram of automaton $\mathcal A=(Q,X,\delta ,\lambda )$ is a directed graph in which the vertices are in bijection with the states of Q and the edges have the form $q\stackrel {x|\lambda (q,x)}{\longrightarrow }\delta (q,x)$ for $q\in Q$ and $x\in X$ . Figure 1 shows the Moore diagram of the automaton $\mathcal A$ that, as is explained later, generates the lamplighter group $\mathcal L=(\mathbb Z/2\mathbb Z)\wr \mathbb Z$ .

Figure 1 Mealy automaton generating the lamplighter group $\mathcal L$ .

Every initial automaton $\mathcal A_{q}$ induces an endomorphism of $X^{*}$ , which is also denoted by $\mathcal A_{q}$ , defined as follows. Given a word $v=x_{1}x_{2}x_{3}\ldots x_{n}\in X^{*}$ , it scans the first letter $x_{1}$ and outputs $\lambda (q,x_{1})$ . The rest of the word is handled similarly by the initial automaton $\mathcal A_{\delta (q,x_{1})}$ . So we can actually extend the functions $\delta $ and $\lambda $ to $\delta \colon Q\times X^{*}\to Q$ and $\lambda \colon Q\times X^{*}\to X^{*}$ via the equations

$$ \begin{align*}\begin{array}{l} \delta(q,x_{1}x_{2}\ldots x_{n})=\delta(\delta(q,x_{1}),x_{2}x_{3}\ldots x_{n}),\\ \lambda(q,x_{1}x_{2}\ldots x_{n})=\lambda(q,x_{1})\lambda(\delta(q,x_{1}),x_{2}x_{3}\ldots x_{n}).\\ \end{array} \end{align*} $$

The boundary $X^{\infty }$ of the tree is endowed with a natural topology in which two infinite words are close if they have a large common prefix. With this topology, $X^{\infty }$ is homeomorphic to the Cantor set. Each endomorphism (respectively automorphism) of $X^{*}$ naturally induces a continuous transformation (respectively homeomorphism) of $X^{\infty }$ .

Definition 2.2. The semigroup (group) generated by all states of an automaton $\mathcal A$ viewed as endomorphisms (automorphisms) of the rooted tree $X^{*}$ under the operation of composition is called an automaton semigroup (group) and is denoted by $\mathbb {S}(\mathcal A)$ (respectively $\mathbb {G}(\mathcal A)$ ).

In the definition of the automaton, we do not require the set Q of states to be finite. With this convention, the notion of an automaton group is equivalent to the notions of a self-similar group [33] and state-closed group [34]. However, most of the interesting examples of automaton (semi)groups are finitely generated (semi)groups defined by finite automata.

Let $g\in \mathop {\mathrm {End}}\nolimits (X^{*})$ and $x\in X$ . For any $v\in X^{*}$ , we can write

$$ \begin{align*}g(xv)=g(x)v^{\prime}\end{align*} $$

for some $v^{\prime }\in X^{*}$ . Then the map $g|_{x}\colon X^{*}\to X^{*}$ given by

$$ \begin{align*}g|_{x}(v)=v^{\prime}\end{align*} $$

defines an endomorphism of $X^{*}$ which we call the state (or section) of g at vertex x. We can inductively extend the definition of a section at a letter $x\in X$ to a section at any vertex $x_{1}x_{2}\ldots x_{n}\in X^{*}$ as follows:

$$ \begin{align*}g|_{x_{1}x_{2}\ldots x_{n}}=g|_{x_{1}}|_{x_{2}}\cdots|_{x_{n}}.\end{align*} $$

We adopt the following convention throughout the paper. If g and h are elements of some (semi)group acting on a set Y and $y\in Y$ , then

$$ \begin{align*}gh(y)=h(g(y)).\end{align*} $$

Hence, the state $g|_{v}$ at $v\in X^{*}$ of any product $g=g_{1}g_{2}\cdots g_{n}$ , where $g_{i}\in \mathop {\mathrm {Aut}}\nolimits (X^{*})$ for $1\leq i\leq n$ , can be computed as follows:

$$ \begin{align*}g|_{v}=g_{1}|_{v} g_{2}|_{g_{1}(v)}\cdots g_{n}|_{g_{1}g_{2}\cdots g_{n-1}(v)}.\end{align*} $$

Also, we use the language of wreath recursions. For each automaton semigroup G, there is a natural embedding

$$ \begin{align*}G\hookrightarrow G \wr \mathop{\mathrm{Tr}}(X),\end{align*} $$

where $\mathop {\mathrm {Tr}}(X)$ denotes the semigroup of all selfmaps of set X. This embedding is given by

(2-1) $$ \begin{align} G\ni g\mapsto (g_{0},g_{1},\ldots,g_{d-1})\sigma_{g}\in G\wr \mathop{\mathrm{Tr}}(X), \end{align} $$

where $g_{0},g_{1},\ldots ,g_{d-1}$ are the states of g at the vertices of the first level and $\sigma _{g}$ is the transformation of X induced by the action of g on the first level of the tree. If $\sigma _{g}$ is the trivial transformation, it is customary to omit it in Equation (2-1). We call $(g_{0},g_{1},\ldots ,g_{d-1})\sigma _{g}$ the decomposition of g at the first level (or the wreath recursion of g). When this does not cause any confusion, we identify g with its wreath recursion and write simply

$$ \begin{align*}g=(g_{0},g_{1},\ldots,g_{d-1})\sigma_{g}.\end{align*} $$

In the case of the automaton group $G=\mathbb {G}(\mathcal A)$ , the embedding Equation (2-1) is actually the embedding into the group $G\wr \mathop {\mathrm {Sym}}\nolimits (X)$ .

The decomposition at the first level of all generators $\mathcal A_{q}$ of an automaton semigroup $\mathbb {S}(\mathcal A)$ under the embedding Equation (2-1) is called the wreath recursion defining the semigroup. Such a decomposition is especially convenient for computing the states of semigroup elements. Indeed, the products endomorphisms and inverses of automorphisms can be found as follows. If $g=(g_{0},g_{1},\ldots ,g_{d-1})\sigma _{g}$ and $h=(h_{0},h_{1},\ldots ,h_{d-1})\sigma _{h}$ are two elements of $\mathop {\mathrm {End}}\nolimits (X^{*})$ , then

$$ \begin{align*}gh=(g_{0}h_{\sigma_{g}(0)},g_{1}h_{\sigma_{g}(1)},\ldots,g_{d-1}h_{\sigma_{g}(d-1)})\sigma_{g}\sigma_{h}\end{align*} $$

and in the case when g is an automorphism, the wreath recursion of $g^{-1}$ is

$$ \begin{align*}g^{-1}=(g^{-1}_{\sigma_{g}^{-1}(0)},g^{-1}_{\sigma_{g}^{-1}(1)},\ldots,g^{-1}_{\sigma_{g}^{-1}(d-1)})\sigma_{g}^{-1}.\end{align*} $$

3 Continuous maps from $\mathbb Z_{d}$ to $\mathbb Z_{d}$

In this section, we recall how to represent every continuous function $f\colon \mathbb Z_{d}\to \mathbb Z_{d}$ by its van der Put series. For details when $d=p$ is prime, we refer the reader to Schikhof’s book [36] and for needed facts about the ring of d-adic integers, we recommend [14, Section 4.2] and [26]. Here we relate the coefficients of these series to the vertices of the rooted d-ary tree, whose boundary is identified with $\mathbb Z_{d}$ .

First, we recall that the ring of d-adic integers $\mathbb Z_{d}$ for arbitrary (not necessarily prime) d is defined as the set of all formal sums

$$ \begin{align*}\mathbb Z_{d}=\{a_{0}+a_{1}d+a_{2}d^{2}+\cdots\,\colon a_{i}\in\{0,1,\ldots,d-1\}=\mathbb Z/d\mathbb Z, i\geq 0\},\end{align*} $$

where addition and multiplication are defined in the same way as in $\mathbb Z_{p}$ for prime p taking into account the carry over. Also, the ring $\mathbb Q_{d}$ of d-adic numbers can be defined as the full ring of fractions of $\mathbb Z_{d}$ , but we only need to use elements of $\mathbb Z_{d}$ below. Algebraically, if $d=p_{1}^{n_{1}}p_{2}^{n_{2}}\cdots p_{k}^{n_{k}}$ is the decomposition of d into the product of primes, then

$$ \begin{align*}\mathbb Z_{d}=\mathbb Z_{p_{1}}\times\mathbb Z_{p_{2}}\times\cdots\times\mathbb Z_{p_{k}}\quad \text{and}\quad \mathbb Q_{d}=\mathbb Q_{p_{1}}\times\mathbb Q_{p_{2}}\times\cdots\times\mathbb Q_{p_{k}}.\end{align*} $$

As stated in the introduction, for the alphabet $X=\{0,1,\ldots ,d-1\}$ , we identify $\mathbb Z_{d}$ with the boundary $X^{\infty }$ of the rooted d-ary regular tree $X^{*}$ in a natural way, viewing a d-adic number $x_{0}+x_{1}d+{x_{2}d^{2}+\cdots }$ as a point $x_{0}x_{1}x_{2}\ldots \in X^{\infty }$ . This identification gives rise to an embedding of $\mathbb N_{0}=\mathbb N\cup \{0\}$ into $X^{*}$ via $n\mapsto [n]_{d}$ , where $[n]_{d}$ denotes the word over X representing the expansion of n in base d written backwards (so that, for example, $[6]_{2}=011$ ). There are two standard ways to define the image $[0]_{d}$ of $0\in \mathbb N_{0}$ : one can define it to be either the empty word $\varepsilon $ over X of length 0 or a word $0$ of length 1. These two choices give rise later to two similar versions of the van der Put bases in the space of continuous functions from $\mathbb Z_{d}$ to $\mathbb Z_{d}$ that we call Mahler and Schikhof versions. Throughout the paper, we use Mahler’s version and, unless otherwise stated, we define $[0]_{d}=0$ (the word of length 1). However, we state some of the results for Schikhof’s version as well. Note that the image of $\mathbb N\cup \{0\}$ consists of all vertices of $X^{*}$ that do not end with $0$ , and the vertex $0$ itself. We call these vertices labeled. For example, the labeling of the binary tree is shown in Figure 2. The inverse of this embedding, with a slight abuse of notation as the notation does not explicitly mention d, we denote by bar $\overline {\phantom a}$ . In other words, if $u=u_{0}u_{1}\ldots u_{n}\in X^{*}$ , then $\overline u=u_{0}+u_{1}d+\cdots +u_{n}d^{n}\in \mathbb N_{0}$ . We note that the operation $u\mapsto \overline u$ is not injective as $\overline u=\overline {u0^{k}}$ for all $k\geq 0$ .

Figure 2 Labeling of vertices of a binary tree by elements of $\mathbb N_{0}$ .

Under this notation, we can also define for each $n\geq 0$ a cylindrical subset $[n]_{d}X^{\infty }\subset \mathbb Z_{d}$ that consists of all d-adic integers that have $[n]_{d}$ as a prefix. Geometrically, this set can be envisioned as the boundary of the subtree of $X^{*}$ hanging down from the vertex $[n]_{d}$ .

For $n>0$ with the d-ary expansion $n=x_{0}+x_{1}d+\cdots +x_{k}d^{k}$ , $x_{k}\neq 0$ , we define $n\_=n-x_{k}d^{k}$ . Geometrically, $n\_$ is the label of the labeled vertex in $X^{*}$ closest to n along the unique path from n to the root of the tree. For example, for $n=22$ , we have $[n]_{2}=01101$ , so $[n\_]_{2}=011$ and $n\_=6$ .

We are ready to define the decomposition of a continuous function $f\colon \mathbb Z_{d}\to \mathbb Z_{d}$ into a van der Put series. For each such function, there is a unique sequence $(B^{f}_{n})_{n\geq 0}$ , $B^{f}_{n}\in \mathbb Z_{d}$ of d-adic integers such that for each $x\in \mathbb Z_{d}$ , the following expansion:

(3-1) $$ \begin{align} f(x)=\sum_{n\geq 0}B^{f}_{n}\chi_{n}(x) \end{align} $$

holds, where $\chi _{n}(x)$ is the characteristic function of the cylindrical set $[n]_{d}X^{\infty }$ with values in $\mathbb Z_{d}$ . The coefficients $B^{f}_{n}$ are called the van der Put coefficients of f and are computed as follows:

(3-2) $$ \begin{align} B^{f}_{n}= \begin{cases} f(n)&\text{if}\ \ 0\leq n<d,\\ f(n)-f(n\_)&\text{if}\ \ n\geq d. \end{cases} \end{align} $$

This is the decomposition with respect to the orthonormal van der Put basis $\{\kern1.2pt \chi _{n}(x)\colon n\geq 0\}$ of the space $C(\mathbb Z_{d})$ of continuous functions from $\mathbb Z_{d}$ (as a $\mathbb Z_{d}$ -module) to itself, as given in Mahler’s book [28], and also used in [5]. In the literature, this basis is considered only when $d=p$ is a prime number, and is, in fact, an orthonormal basis of a larger space $C(\mathbb Z_{p}\to K)$ of continuous functions from $\mathbb Z_{p}$ to a normed field K containing the field of p-adic rationals $\mathbb Q_{p}$ . However, the given decomposition works in our context with all the proofs identical to the ‘field’ case.

To avoid possible confusion, we note that there is another standard version of the van der Put basis $\{\tilde \chi _{n}(x)\colon n\geq 0\}$ used, for example, in Schikhof’s book [36]. We call this version of a basis Schikhof’s version. In this basis, $\tilde \chi _{n}=\chi _{n}$ for $n>0$ , and $\tilde \chi _{0}$ is the characteristic function of the whole space $\mathbb Z_{d}$ (while $\chi _{0}$ is the characteristic function of $d\mathbb Z_{d}=0X^{\infty }$ ). This differencecorresponds to two ways of defining $[0]_d$ as mentioned earlier, since $\chi_n$ is defined as the characteristic function of $[n]_d X_\infty$ . The definition of $\chi 0$ clearly depends on the choice we make for $[0]_d$ .If $[0]_{d}=0$ , we obtain the version of basis used by Mahler, and defining $[0]_{d}=\varepsilon $ (the empty word) yields the basis used by Schikhof. This difference does not change much the results and the proofs, and we give formulations of some of our results for both bases. In particular, the decomposition Equation (3-1) is transformed into

$$ \begin{align*} f(x)=\sum_{n\geq 0}\tilde B^{f}_{n}\tilde\chi_{n}(x), \end{align*} $$

where Schikhof’s versions of the van der Put coefficients $\tilde B^{f}_{n}$ are computed as

$$ \begin{align*} \tilde B^{f}_{n}= \begin{cases} f(0)&\text{if}\ \ n=0,\\ f(n)-f(n\_)&\text{if}\ \ n>0. \end{cases} \end{align*} $$

Among all continuous functions $\mathbb Z_{d}\to \mathbb Z_{d}$ , we are interested in those that define endomorphisms of $X^{*}$ (viewed as a tree). We use the following useful characterization of these maps in terms of the coefficients of their van der Put series (which works for both versions of the van der Put basis). In the case of prime d, this easy fact is given in [5]. The proof in the general case is basically the same and we omit it.

Theorem 3.1. A function $\mathbb Z_{d}\to \mathbb Z_{d}$ is $1$ -Lipschitz if and only if it can be represented as

(3-3) $$ \begin{align} f(x)=\sum_{n\geq 0}b^{f}_{n}d^{\lfloor\log_{d}n\rfloor}\chi_{n}(x), \end{align} $$

where $b^{f}_{n}\in \mathbb Z_{d}$ for all $n\geq 0$ , and

$$ \begin{align*}\lfloor \log_{d}n\rfloor= (\text{the number of digits in the base-}\textit{d}\text{ expansion of}\ n)-1.\end{align*} $$

We call the coefficients $b^{f}_{n}$ from Theorem 3.1 the reduced van der Put coefficients. It follows from Equation (3-2) that these coefficients are computed as

(3-4) $$ \begin{align} b^{f}_{n}=B^{f}_{n} d^{-\lfloor\log_{d}n\rfloor}= \begin{cases} f(n)&\text{if}\ \ 0\leq n<d,\\[2mm] \dfrac{f(n)-f(n\_)}{d^{\lfloor\log_{d}n\rfloor}}&\text{if}\ \ n\geq d. \end{cases} \end{align} $$

For Schikhof’s version of the van der Put basis, Equation (3-3) has to be replaced with

$$ \begin{align*}f(x)=\sum_{n\geq 0}\tilde {b}^{f}_{n}d^{\lfloor\log_{d}n\rfloor}\chi_{n}(x)\end{align*} $$

and the corresponding reduced van der Put coefficients are computed as

$$ \begin{align*}\tilde {b}^{f}_{n}=\tilde B^{f}_{n} d^{-\lfloor\log_{d}n\rfloor}= \begin{cases} f(0)&\text{if}\ \ n=0,\\[2mm] \dfrac{f(n)-f(n\_)}{d^{\lfloor\log_{d}n\rfloor}}&\text{if}\ \ n>0. \end{cases} \end{align*} $$

In particular, $\tilde {b}^{f}_{n}=b^{f}_{n}$ for all $n\geq d$ .

We note that since Schikhof’s reduced van der Put coefficients $\tilde {b}^{f}_{n}$ differ from $b^{f}_{n}$ only for $n<d$ , the claim of Theorem 1.1 clearly remains true for Schikhof’s van der Put series as well.

4 Automatic sequences

There are several equivalent ways to define d-automatic sequences. We refer the reader to Allouche–Shallit’s book [2] for details. Informally, a sequence $(a_{n})_{n\geq 0}$ is called d-automatic if one can compute $a_{n}$ by feeding a deterministic finite automaton with output (DFAO) as the base-d representation of n, and then applying the output mapping $\tau $ to the last state reached. We first recall the definition of the (Moore) DFAO and then give the formal definition of automatic sequences.

Definition 4.1. A deterministic finite automaton with output (or a Moore automaton) is defined to be a 6-tuple

$$ \begin{align*}\mathcal B=(Q,X,\delta,q_{0},A,\tau),\end{align*} $$

where

• • Q is a finite set of states;

• • X is the finite input alphabet;

• • $\delta \colon Q\times X\to Q$ is the transition function;

• • $q_{0}\in Q$ is the initial state;

• • A is the output alphabet;

• • $\tau \colon Q\to A$ is the output function.

In the case when the input alphabet is $X=\{0,1,\ldots ,d-1\}$ , we call the corresponding automaton a d-DFAO.

Similar to the case of Mealy automata, we extend the transition function $\delta $ to $\delta \colon Q\times X^{*}\to Q$ . With this convention, a d-DFAO defines a function $f_{M}\colon X^{*}\to A$ by $f_{M}(w)=\tau (\delta (q_{0},w))$ .

Note that Moore automata can also be viewed as transducers as well by recording the values of the output function at every state while reading the input word. This way, each word over X is transformed into a word over A of the same length. This model of calculations is equivalent to Mealy automata (in the more general case when the output alphabet is allowed to be different from the input alphabet) in the sense that for each Moore automaton, there exists a Mealy automaton that defines the same transformation from $X^{*}$ to $A^{*}$ and vice versa (see [37] for details).

Recall that for a word $w=x_{0}x_{1}\ldots x_{n}\in X^{*}$ , we write $\overline w=x_{0}+x_{1}d+\cdots +x_{n}d^{n}\in \mathbb N_{0}$ for the label of the labeled vertex in $X^{*}$ closest to w along the unique path from w to the root of the tree.

Definition 4.2 [2]

We say that a sequence $(a_{n})_{n\geq 0}$ over a finite alphabet A is d-automatic if there exists a d-DFAO $\mathcal B=(Q,X,\delta ,q_{0},A,\tau )$ such that $a_{n}=\tau (\delta (q_{0},w))$ for all $n\geq 0$ and $w\in X^{*}$ with $\overline w=n$ .

For us, it is more convenient to use the alternative characterization of automatic sequences (for the proof, see for instance [2]).

Theorem 4.3. A sequence $(a_{n})_{n\geq 0}$ over an alphabet A is d -automatic if and only if the collection of its subsequences of the form $\{(a_{j+n\cdot d^{i}})_{n\geq 0}\mid i\geq 0, 0\leq j<d^{i}\}$ , called the d-kernel, is finite.

We recall the connection between the d-DFAO defining a d-automatic sequence $(a_{n})_{n\geq 0}$ and the d-kernel of this sequence (see Theorem 6.6.2 in [2]). For that, we define the section of a sequence $(a_{n})_{n\geq 0}$ at a word v over $X=\{0,1,\ldots ,d-1\}$ recursively as follows.

Definition 4.4. Let $(a_{n})_{n\geq 0}$ be a sequence over alphabet A. Its d-section $(a_{n})_{n\geq 0}|_{x}$ at $x\in X=\{0,1,\ldots ,d-1\}$ is a subsequence $(a_{x+nd})_{n\geq 0}$ . For a word $v=x_{1}x_{2}\ldots x_{k}$ over X, we further define the d-section $(a_{n})_{n\geq 0}|_{v}$ at v to be either $(a_{n})_{n\geq 0}$ itself if v is the empty word or $(a_{n})_{n\geq 0}|_{x_{1}}|_{x_{2}}\cdots |_{x_{k}}$ otherwise.

We often omit d in the term d-section when d is clear from the context. The d-kernel of a sequence consists exactly of d-sections and the d-automaticity of a sequence can be reformulated as follows.

Proposition 4.5. A sequence $(a_{n})_{n\geq 0}$ over an alphabet A is d-automatic if and only if the set $\{(a_{n})_{n\geq 0}|_{v} : v\in X^{*}\}$ is finite.

The subsequences involved in the definition of the d-kernel can be plotted on the d-ary rooted tree $X^{*}$ , where the vertex $v\in X^{*}$ is labeled with the subsequence $(a_{n})|_{v}$ . For $d=2$ , such a tree is shown in Figure 3.

Figure 3 Tree of subsequences of $(a_{n})_{n\geq 0}$ constituting its d-kernel (for $d=2$ ).

A convenient way to represent sections of a sequence and understand d-automaticity is to put the terms of this sequence on a d-ary tree. Recall that in the previous section, we have constructed an embedding of $\mathbb N_{0}$ into $X^{*}$ via $n\mapsto [n]_{d}$ . Under this embedding, we call the image of $n\in \mathbb N\cup \{0\}$ the vertex n of $X^{*}$ .

Definition 4.6. The d-portrait of a sequence $(a_{n})_{n\geq 0}$ over an alphabet A is a d-ary rooted tree $X^{*}$ , where the vertex n is labeled by $a_{n}$ and other vertices are unlabeled.

In other words, we label each vertex $v=x_{0}x_{1}\ldots x_{k}$ with $x_{k}\neq 0$ or $v=0$ by $a_{\overline {v}}=a_{x_{0}+x_{1}d+\cdots +x_{k}d^{k}}$ . For example, Figure 4 represents the 2-portrait of the sequence $(a_{n})_{n\geq 0}$ .

Figure 4 The 2-portrait of the sequence $(a_{n})_{n\geq 0}$ .

To simplify the exposition, we write simply portrait for d-portrait when the value of d is clear from the context. In particular, unless otherwise stated, X denotes an alphabet $\{0,1,\ldots ,d-1\}$ of cardinality d and a portrait means a d-portrait.

There is a simple connection between the portrait of a sequence and the portrait of its section at vertex $v\in X^{*}$ that takes into account that the subtree $vX^{*}$ of $X^{*}$ hanging down from vertex v is canonically isomorphic to $X^{*}$ itself via $vu\leftrightarrow u$ for each $u\in X^{*}$ .

Proposition 4.7. For a sequence $(a_{n})_{n\geq 0}$ over an alphabet A with a portrait P and a vertex $v=x_{0}x_{1}\ldots x_{k}$ , $k\geq 0$ of $X^{*}$ , the portrait of the section $(a_{n})_{n\geq 0}|_{v}$ is obtained from the portrait of $(a_{n})_{n\geq 0}$ by taking the (labeled) subtree of P hanging down from vertex v, removing, if v ends with $x_{k}\neq 0$ and $k>0$ , the label at its root vertex, and labeling the vertex 0 by $a_{\overline {v}}=a_{x_{0}+x_{1}d+\cdots +x_{k}d^{k}}$ , which is the label of the labeled vertex in P closest to $v0$ on the unique path connecting $v0$ to the root.

The proof of the above proposition follows immediately from the definitions of portrait and section.

In other words, as shown in Figure 4, you can see the portrait of a section of a sequence $(a_{n})_{n\geq 0}$ at vertex $v\in X^{*}$ just by looking at the subtree hanging down in the portrait of $(a_{n})_{n\geq 0}$ from vertex v (modulo the minor technical issue of labeling the vertex $0$ of this subtree and possibly removing the label of the root vertex). Therefore, a sequence is automatic if and only if its portrait has a finite number of ‘subportraits’ hanging down from its vertices. This way of interpreting automaticity now corresponds naturally to the condition of an automaton endomorphism being finite state.

Note that the formulation of the previous proposition would be simpler had we defined portraits by labeling each vertex $v=x_{0}x_{1}\ldots x_{k}$ of the tree by $a_{x_{0}+x_{1}d+\cdots x_{k}d^{k}}$ instead of only numbered ones, but we intentionally opt not to do that, to simplify our notation in the next section.

Now it is easy to see that the d-DFAO defining a d-automatic sequence $(a_{n})_{n\geq 0}$ over an alphabet A with the d-kernel K can be built as follows.

Proposition 4.8. Suppose $(a_{n})_{n\geq 0}$ is a d-automatic sequence over an alphabet A with the d-kernel K. Then a d-DFAO $\mathcal B=(K,X,\delta ,q_{0},A,\tau )$ , where

(4-1) $$ \begin{align} \begin{aligned} \delta((a_{n})_{n\geq0}|_{v}, x)&=(a_{n})_{n\geq0}|_{vx},\\ \tau((a_{n})_{n\geq0}|_{v})&=a_{\overline{v}}\ (\text{the first term of the sequence}\ (a_{n})_{n\geq0}|_{v}),\\ q_{0}&=(a_{n})_{n\geq0}|_{\varepsilon}=(a_{n})_{n\geq0} \end{aligned} \end{align} $$

defines the sequence $(a_{n})_{n\geq 0}$ .

Informally, we build the automaton M by following the edges of the tree $X^{*}$ from the root, labeling these edges by the corresponding elements of X, and identifying the vertices that correspond to the same sections of $(a_{n})_{n\geq 0}$ into one state of M that is labeled by the $0$ th term of the corresponding section.

5 Portraits of sequences of reduced van der Put coefficients and their sections

It turns out that there is a natural relation between the (portraits of the sequences of) reduced van der Put coefficients of an endomorphism g and of its sections. Denote by $\sigma \colon \mathbb Z_{d}\to \mathbb Z_{d}$ the map $\sigma (a)=({a-(a\,\mathrm {mod}\, d)})/d$ . This map corresponds to the shift map on $\mathbb Z_{d}$ that deletes the first letter of a. That is, if $a=x_{0}x_{1}x_{2}\ldots \in \mathbb Z_{d}$ , then $\sigma (a)=x_{1}x_{2}x_{3}\ldots \in \mathbb Z_{d}$ .

Theorem 5.1. Suppose $g\in \mathop {\mathrm {End}}\nolimits X^{*}$ has sections $g|_{x}$ , $x=0,1,\ldots ,n-1$ at the vertices of the first level of $X^{*}$ . Then the reduced van der Put coefficients $b_{n}^{g|_{x}}$ of the section $g|_{x}$ satisfy:

(5-1) $$ \begin{align} b_{n}^{g|_{x}}=\begin{cases} \sigma(b_{x}^{g})& n=0,\\ b_{x+nd}^{g}+\sigma(b_{x}^{g})& 0<n<d,\\ b_{x+nd}^{g}& n\geq d, \end{cases} \end{align} $$

where for $b\in \mathbb Z_{d}$ , we denote by $\sigma (b)=({b-(b\,\mathrm {mod}\, d)})/d$ the shift map on $\mathbb Z_{d}$ .

Proof. First we consider the case $n=0$ . By Equation (3-4), the reduced van der Put coefficients are computed as follows:

$$ \begin{align*}b_{0}^{g|_{x}}=g|_{x}(0^{\infty})=\frac{g(x0^{\infty})-(g(x0^{\infty})\,\mathrm{mod}\, d)}d=\sigma(g(x0^{\infty}))=\sigma(b_{x}^{g}).\end{align*} $$

Similarly for $0<n<d$ , we obtain

$$ \begin{align*}b_{n}^{g|_{x}}&=g|_{x}(n0^{\infty})=\frac{g(xn0^{\infty})-(g(xn0^{\infty})\,\mathrm{mod}\, d)}d\\ &=\frac{g(xn0^{\infty})-(g(x0^{\infty})\,\mathrm{mod}\, d)}d+\frac{g(x0^{\infty})-(g(xn0^{\infty})\,\mathrm{mod}\, d)}d\\ &=b_{x+nd}^{g}+\frac{g(x0^{\infty})-(g(x0^{\infty})\,\mathrm{mod}\, d)}d=b_{x+nd}^{g}+\sigma(b_{x}^{g}). \end{align*} $$

Finally, for $n>d$ , we derive

$$ \begin{align*}b_{n}^{g|_{x}}&=d^{-\lfloor\log_{d}n\rfloor}(g|_{x}([n]_{d}0^{\infty})-g|_{x}([n\_]_{d}0^{\infty}))\\ &=d^{-\lfloor\log_{d}n\rfloor}\bigg(\frac{g(x[n]_{d}0^{\infty})-(g(x[n]_{d}0^{\infty})\,\mathrm{mod}\, d)}d\\&\qquad\quad\qquad-\frac{g(x[n\_]_{d}0^{\infty})-(g(x[n\_]_{d}0^{\infty})\,\mathrm{mod}\, d)}d\bigg)\\ &=d^{-\lfloor\log_{d}n\rfloor-1}(g(x[n]_{d}0^{\infty})-g(x[n\_]_{d}0^{\infty}))\\ &=d^{-\lfloor\log_{d}(x+nd)\rfloor}(g([x+nd]_{d}0^{\infty})-g([(x+nd)\_]_{d}0^{\infty}))=b_{x+nd}^{g}, \end{align*} $$

where in the last line, we used that for $x<d$ , we have $x+(n\_)d=(x+nd)\_$ and

$$ \begin{align*}\lfloor\log_{d}(n)\rfloor+1=\lfloor\log_{d}(n)+1\rfloor=\lfloor\log_{d}(nd)\rfloor=\lfloor\log_{d}(x+nd)\rfloor.\\[-38pt]\end{align*} $$

In the case of Schikhof’s version of the van der Put basis, we can similarly prove the following.

Theorem 5.2. Suppose $g\in \mathop {\mathrm {End}}\nolimits X^{*}$ has sections $g|_{x}$ , $x=0,1,\ldots ,n-1$ at the vertices of the first level of $X^{*}$ . Then the reduced van der Put coefficients with respect to Schikhof’s version of the van der Put basis of the section $g|_{x}$ satisfy:

$$ \begin{align*} \tilde {b}_{n}^{g|_{x}}=\begin{cases}{ll} \sigma(\tilde {b}_{0}^{g})& n=0, x=0,\\ \sigma(\tilde {b}_{x}^{g}+b_{0}^{g})& n=0, 0<x<d,\\ \tilde {b}_{x+nd}^{g}& n>0. \end{cases} \end{align*} $$

There is a more visual way to state the third case in Equation (5-1) using the $\overline {\phantom {a}}$ notation.

Corollary 5.3. Let $x_{0}x_{1}\ldots x_{k}\in X^{*}$ be a word of length $k+1\geq 3$ with $x_{k}\neq 0$ . Then,

$$ \begin{align*}b^{g}_{\overline{x_{0}x_{1}\ldots x_{k}}}=b^{g|_{x_{0}}}_{\overline{x_{1}\ldots x_{k}}}.\end{align*} $$

Proof. Follows from Equation (5-1) and the fact that if $\overline {x_{1}x_{2}\ldots x_{k}}=n$ , then $\overline {x_{0}x_{1}x_{2}\ldots x_{k}}=x_{0}+nd$ .

The next corollary is used in the calculations in Section 8.

Corollary 5.4. Let $v,w\in X^{*}$ with w of length at least $2$ and ending in a nonzero element of X. Then,

$$ \begin{align*}b^{g}_{\overline{vw}}=b^{g|_{v}}_{\overline{w}}.\end{align*} $$

Proof. When v is the empty word, the claim is trivial. The general case now follows by induction on $|v|$ from Corollary 5.3 as for each $x\in X$ , we have

$$ \begin{align*}b^{g}_{\overline{xvw}}=b^{g|_{x}}_{\overline{vw}}=b^{(g|_{x})|_{v}}_{\overline{w}}=b^{g|_{xv}}_{\overline{w}}.\\[-37pt]\end{align*} $$

Corollary 5.5. Let $g\in \mathop {\mathrm {End}}\nolimits (X^{*})$ be an endomorphism of $X^{*}$ and $v\in X^{*}$ be an arbitrary vertex. Then the sequences $(b_{n}^{g|_{v}})_{n\geq 0}$ and $(b_{n}^{g})_{n\geq 0}|_{v}$ coincide starting from term d.

Proof. For any $n\geq d$ , we have that $[n]_{d}=xw$ for some $x\in X$ and $w\in X^{*}$ of length at least 1 that ends with a nonzero element of X. So we have by Corollary 5.4,

$$ \begin{align*}b_{n}^{g|_{v}}=b_{\overline{xw}}^{g|_{v}}=b_{\overline{vxw}}^{g}.\end{align*} $$

However, $b_{\overline {vxw}}^{g}$ is exactly the term of the sequence $(b_{n}^{g})_{n\geq 0}|_{v}$ with index $n=\overline {xw}$ .

Now, taking into account Proposition 4.7, there is a geometric way to look at the previous theorem. Namely, the third subcase in Equation (5-1) yields the following proposition.

Corollary 5.6. Let $v\in X^{*}$ be an arbitrary vertex of $X^{*}$ . The labels of the portrait of the sequence $(b_{n}^{g|_{v}})_{n\geq 0}$ coincide at levels $2$ and below with the corresponding labels of the restriction of the portrait of $(b_{n}^{g})_{n\geq 0}$ to the subtree hanging down from vertex $v\in X$ .

We illustrate by Figure 5 this fact for $v=x\in X$ of length one, where the portraits of $(b_{n}^{g|_{0}})_{n\geq 0}$ and $(b_{n}^{g|_{1}})_{n\geq 0}$ are drawn on the left and right subtrees of the portrait of $(b_{n}^{g})_{n\geq 0}$ . Figure 5 demonstrates that the labels of the portraits of sections coincide with the labels of the portrait of $(b_{n}^{g})_{n\geq 0}$ below the dashed line. The first two subcases of Equation (5-1) give labels of the portraits of $(b_{n}^{g|_{x}})_{n\geq 0}, x\in X$ on the first level.

Figure 5 Correspondence between portraits of $(b_{n}^{g|_{x}})_{n\geq 0}$ and $(b_{n}^{g})_{n\geq 0}$ .

6 Proof of the Theorem 1.1

In this section, we prove Theorem 1.1. In the arguments below, we work with eventually periodic elements of $\mathbb Z_{d}$ , that is, elements of the form $a_{0}+a_{1}d+a_{2}d^{2}+\cdots $ with eventually periodic sequences $(a_{i})_{i\geq 0}$ of coefficients. As shown in [14, Theorem 4.2.4], this set of d-adic integers can be identified with the subset $\mathbb Z_{d,0}$ of $\mathbb Q$ consisting of all rational numbers $a/b\in \mathbb Q$ such that b is relatively prime to d. Algebraically, it can be defined as $\mathbb Z_{d,0}=D^{-1}\mathbb Z$ , where D is the multiplicative set $\{b\in \mathbb Z\colon \gcd (b,d)=1\}$ . We denote the corresponding inclusion $\mathbb Z_{d,0}\hookrightarrow \mathbb Z_{d}$ by $\psi $ . The following inclusions then take place:

$$ \begin{align*}\begin{array}{ccccccc} \mathbb Z&\subset&\mathbb Z_{d,0}&\stackrel{\psi}{\hookrightarrow}&\mathbb Z_{d}&\subset&\mathbb Q_{d}\\ &&\cap&&\\ &&\mathbb Q&& \end{array} \end{align*} $$

We do not need the definition of $\psi $ which can be constructed using lemma 4.2.2 in [14], but rather need the definition of $\psi ^{-1}\colon \psi (\mathbb Z_{d,0})\to \mathbb Z_{d,0}$ . The map is defined as follows. Suppose $uv^{\infty }\in \mathbb Z_{d}$ is an arbitrary eventually periodic element for some ${u,v\in X^{*}}$ . Then we define

$$ \begin{align*}\psi^{-1}(uv^{\infty})=\overline u+\frac{\overline v\cdot d^{|u|}}{1-d^{|v|}}\in\mathbb Z_{d,0}.\end{align*} $$

Lemma 6.1. The preimage under $\psi $ of the set $\{v^{\infty }\colon v\in X^{m}\}$ of all periodic elements of $\mathbb Z_{d}$ whose periods have lengths dividing $m\geq 0$ is the set

$$ \begin{align*}P^{0,m}=\bigg\{\frac j{1-d^{m}}\colon 0\leq j<d^{m}\bigg\},\end{align*} $$

which is a subset of the interval $[-1,0]\subset \mathbb R$ .

Proof. It follows from the definition of $\psi ^{-1}$ that

$$ \begin{align*}\psi^{-1}(v^{\infty})= \frac{\overline v}{1-d^{|v|}}.\end{align*} $$

Recall that for $v=x_{0}x_{1}\ldots x_{m-1}$ , we have $\overline v=x_{0}+x_{1}d+\cdots +x_{m-1}d^{m-1}$ . This implies that $0\leq \overline v\leq d^{m}-1$ and, henceforth, $-1\leq \psi ^{-1}(v^{\infty })\leq 0$ . Moreover, as v runs over all words in $X^{m}$ , $\overline v$ runs over all integer numbers from $0$ to $d^{m}-1$ as we simply list the d-ary expansions of all these numbers.

Lemma 6.2. The preimage under $\psi $ of the set $\{uv^{\infty }\colon u\in X^{l}, v\in X^{m}\}$ of all eventually periodic elements of $\mathbb Z_{d}$ with preperiods of length at most $l\geq 0$ and periods of lengths dividing $m\geq 1$ is the set

$$ \begin{align*}P^{l,m}=\bigg\{i+\frac{j\cdot d^{l}}{1-d^{m}}\colon 0\leq i<d^{l}, 0\leq j<d^{m}\bigg\},\end{align*} $$

which is a subset of the interval $[-d^{l},d^{l}-1]\subset \mathbb R$ .

Proof. We have

$$ \begin{align*} \psi^{-1}(\{uv^{\infty}\colon u\in X^{l},v\in X^{m}\})&=\{\psi^{-1}(uv^{\infty})\colon u\in X^{l},v\in X^{m}\}\\ &=\{\psi^{-1}(u0^{\infty})+\psi^{-1}(0^{l}v^{\infty})\colon u\in X^{l},v\in X^{m}\}\\&=\{\overline u+d^{l}\cdot\psi^{-1}(v^{\infty})\colon u\in X^{l},v\in X^{m}\}\\ &=\{i+d^{l}\psi^{-1}(v^{\infty})\colon 0\leq i<d^{l},v\in X^{m}\}=\bigcup_{0\leq i<d^{l}}(i+d^{l}P^{0,m}). \end{align*} $$

The set $d^{l}P^{0,m}$ by Lemma 6.1 is a subset of $[-d^{l},0]$ . Therefore, since $P^{l,m}\subset \mathbb Q$ is obtained as the union of all shifts of $d^{l}P^{0,m}$ by all integers $0\leq i<d^{l}$ , we obtain that $P^{l,m}\subset [-d^{l},d^{l}-1]$ .

To obtain the condition of finiteness of Mealy automata in the proof of Theorem 1.1, we also need the following technical lemma. Define a sequence of subsets $A_{i}^{l,m}$ recursively by $A_{0}^{l,m}=P^{l,m}$ , and

(6-1) $$ \begin{align} A_{i+1}^{l,m}=\sigma(A_{i}^{l,m})+P^{l,m}. \end{align} $$

$A^{l,m}_{i}$ is used later to describe the possible sets of states of an automaton defined by a transformation with a given automatic sequence of reduced van der Put coefficients.

Lemma 6.3. The set $A^{l,m}=\bigcup _{i\geq 0}A^{l,m}_{i}$ is finite.

Proof. First, we remark that the denominators of the fractions in $A^{l,m}_{i}$ are divisors of $d^{m}-1$ . Therefore, it is enough to prove by induction on i that $A^{l,m}_{i}\subset [-z,z]$ for $z=({d^{l+1}+d-1})/({d-1})$ . For $i=0$ , the statement is true since $A_{0}^{l,m}\subset [-d^{l},d^{l}-1]$ by Lemma 6.1, and

$$ \begin{align*}z=\frac{d^{l+1}+d-1}{d-1}>\frac{d^{l+1}+d-1}{d}=d^{l}+\frac{d-1}d>d^{l}.\end{align*} $$

Assume that the statement is true for a given $i\geq 0$ . Any element of $A_{i+1}^{l,m}$ is equal to $\sigma (x)+b$ for some $x\in A_{i+1}^{l,m}\subset [-z,z]$ and $b\in P^{l,m}\subset [-d^{l},d^{l}-1]$ . Since $\sigma (x)=({x-x\,\mathrm {mod}\, d})/d$ , we immediately obtain

$$ \begin{align*}\sigma(x)+b&\leq\frac xd+b\leq \frac zd+d^{l}-1=\frac{(d^{l+1}+d-1)}{d(d-1)}+d^{l}-1\\&=\frac{d^{l}+1+(d^{l}-1)(d-1)}{d-1}=\frac{d^{l+1}-d+2}{d-1}<z. \end{align*} $$

For the lower bound, we obtain

$$ \begin{align*}\sigma(x)+b&\geq\frac {x-d+1}d+b\geq \frac{-z-d+1}d-d^{l}=\frac{-\frac{d^{l+1}+d-1}{d-1}-d+1}{d}-d^{l}\\ &=\frac{-d^{l}-d+1}{d-1}-d^{l}=-\frac{d^{l+1}+d-1}{d-1}=-z.\\[-3.3pc] \end{align*} $$

We are ready to proceed to the main result of this section.

Proof of Theorem 1.1.

First, assume that $g\in \mathop {\mathrm {End}}\nolimits (X^{*})$ is defined by a finite Mealy automaton $\mathcal A$ with the set of states Q. To prove that $(b^{g}_{n})_{n\geq 0}$ is automatic, by Proposition 4.5, we need to show that it has finitely many sections at vertices of $X^{*}$ .

Assume that $v\in X^{*}$ is of length at least 2, $v=v^{\prime }xy$ for some $v^{\prime }\in X^{*}$ and $x,y\in X$ . Then the section $(b^{g}_{n})|_{v}$ is a sequence that can be completely identified by a pair

(6-2) $$ \begin{align} (b^{g}_{\overline v},\sigma((b^{g}_{n})|_{v})), \end{align} $$

where $b^{g}_{\overline v}$ is its zero term, and $\sigma ((b^{g}_{n})|_{v})$ is the subsequence made of all other terms.

Since by Corollary 5.6

$$ \begin{align*}\sigma((b^{g}_{n})|_{v})=\sigma((b^{g}_{n})|_{v^{\prime}xy})=\sigma((b^{g|_{v^{\prime}}}_{n})|_{xy}),\end{align*} $$

the number of possible choices for the second component in Equation (6-2) is bounded above by $|Q|\cdot |X|^{2}$ (as we have $|Q|$ choices for $g|_{v^{\prime }}$ and $|X|^{2}$ choices for $xy\in X^{2}$ ).

Further, if $\overline v<d$ (that is, $v=z0^{k}$ for some $z\in X$ ), then the number of choices for the first component $b^{g}_{\overline v}$ of Equation (6-2) is bounded above by $|Q|\cdot |X|$ . Otherwise, $v^{\prime }=v^{\prime \prime }x^{\prime }y^{\prime }$ for some $v^{\prime \prime }\in X^{*}$ , $x^{\prime },y^{\prime }\in X$ with $y^{\prime }\neq 0$ . In this case, $b^{g}_{\overline v}=b^{g|_{v^{\prime \prime }}}_{\overline {x^{\prime }y^{\prime }}}$ , so the number of possible choices for $b^{g}_{\overline v}$ is again bounded above by $|Q|\cdot |X|^{2}$ . Thus, the sequence $(b^{g}_{n})_{n\geq 0}$ has finitely many sections.

To prove the first condition asserting that all $b^{g}_{n}$ are in $\mathbb Z_{d}\cap \mathbb Q$ , or, equivalently, eventually periodic, it is enough to mention that by Equation (3-4) $b^{g}_{n}$ must be eventually periodic for $n\geq d$ as a shifted difference of two eventually periodic words $g(n)=g([n]_{d}0^{\infty })$ and $g(n\_)=g([n\_]_{d}0^{\infty })$ . The latter two words are eventually periodic as they are the images of eventually periodic words $[n]_{d}0^{\infty }$ and $[n\_]_{d}0^{\infty }$ under a finite automaton transformation. A similar argument works for $n<d$ , in which case there is no need to take a difference.

Now we prove the converse direction. Assume that for an endomorphism ${g\in \mathop {\mathrm {End}}\nolimits (X^{*})}$ of $X^{*}$ , the sequence $(b^{g}_{n})_{n\geq 0}$ is automatic and consists of eventually periodic elements of $\mathbb Z_{d}$ . Then automaticity implies that $\{b^{g}_{n} : n\geq 0\}$ is finite as a set. Let l be the maximal length among the preperiods of all $b^{g}_{n}$ and let m be the least common multiple of the lengths of all periods of $b^{g}_{n}$ . Then clearly $b^{g}_{n}\in \psi (P^{l,m})$ for all $n\geq 0$ by the definition of $P^{l,m}$ given in Lemma 6.2.

Our aim is to show that the set $\{g|_{v} : v\in X^{*}\}$ is finite. We show that there are only finitely many portraits $(b^{g|_{v}}_{n})_{n\geq 0}$ . Let $v\in X^{*}$ . By Corollary 5.6, the part of the portrait of $(b^{g|_{v}}_{n})_{n\geq 0}$ below level one coincides with the part below level one of the restriction of the portrait of $(b^{g}_{n})_{n\geq 0}$ on the subtree hanging down from vertex v. However, according to Propositions 4.5 and 4.7, since $(b^{g}_{n})_{n\geq 0}$ is automatic, there is only a finite number of such restrictions as the set of all sections $\{(b^{g}_{n})|_{v}: v\in X^{*}\}$ is finite.

Hence, we only need to check that there is a finite number of choices for the van der Put coefficients of the first level of $g|_{v}$ for $v\in X^{*}$ . To do that, we prove by induction on $|v|$ that $b^{g|_{v}}_{i}\in \psi (A^{l,m}_{|v|})$ for $0\leq i<d$ . The claim is trivial for $|v|=0$ by definition of $A^{l,m}$ and the choice of l and m. Assume that the claim is true for all words v of length k, and let $vx$ be a word of length $k+1$ for some $x\in X$ . Then by assumption, $b^{g|_{v}}_{x}\in \psi (A^{l,m}_{|v|})$ and additionally $b^{g|_{v}}_{x+d\cdot i}\in P^{l,m}$ for $1\leq i<d$ , as these coefficients of g on the second level of its portrait coincide with the corresponding coefficients of g. Now by Theorem 5.1, we obtain

$$ \begin{align*} b_{i}^{g|_{vx}}=b_{i}^{(g|_{v})|_{x}}= \begin{cases} \sigma(b_{x}^{g|_{v}})& i=0,\\ b_{x+d\cdot i}^{g|_{v}}+\sigma(b_{x}^{g|_{v}})& 0<i<d. \end{cases} \end{align*} $$

In both cases, we get that $b_{i}^{g|_{vx}}\in A^{l,m}_{|vx|}$ by definition of $A^{l,m}_{|vx|}$ from Equation (6-1). Finally, Lemma 6.3 now guarantees that g has finitely many sections and completes the proof.

7 Mealy and Moore automata associated with an endomorphism of $X^{*}$

The above proof of Theorem 1.1 allows us to build algorithms that construct the Moore automaton of the automatic sequence of reduced van der Put coefficients of a transformation of $\mathbb Z_{d}$ defined by a finite state Mealy automaton, and vice versa.

We start from constructing the Moore automaton generating the sequence of reduced van der Put coefficients of an endomorphism g from the finite Mealy automaton defining g.

Theorem 7.1. Let $g\in \mathop {\mathrm {End}}\nolimits (X^{*})$ be an endomorphism of $X^{*}$ defined by a finite initial Mealy automaton $\mathcal A$ with the set of states $Q_{\mathcal A}=\{g|_{v}\colon v\in X^{*}\}$ . Let also $(b_{n}^{g})_{n\geq 0}$ be the sequence of reduced van der Put coefficients of the map $\mathbb Z_{d}\to \mathbb Z_{d}$ induced by g. Then the Moore automaton $\mathcal B=(Q_{\mathcal B},X,\delta ,q,\mathbb Z_{d},\tau )$ , where

• • the set of states is $Q_{\mathcal B}=\{(g|_{v},(b^{g}_{\overline {vy}})_{y\in X})\colon v\in X^{*}\}$ ;

• • the transition and output functions are

  (7-1) $$ \begin{align} \begin{aligned} \delta((g|_{v},(b^{g}_{\overline{vy}})_{y\in X}),x)&=(g|_{vx},(b^{g}_{\overline{vxy}})_{y\in X}),\\ \tau((g|_{v},(b^{g}_{\overline{vy}})_{y\in X}))&=b^{g}_{\overline{v}}; \end{aligned} \end{align} $$

• • the initial state is $q=(g,(b^{g}_{\overline {y}})_{y\in X})$ ,

is finite, and generates the sequence $(b_{n}^{g})_{n\geq 0}$ .

Proof. According to Proposition 4.8, one can construct an automaton $\mathcal B^{\prime }$ generating $(b_{n}^{g})_{n\geq 0}$ as follows. The states of $\mathcal B^{\prime }$ are the sections of $(b_{n}^{g})_{n\geq 0}$ at the vertices of $X^{*}$ (that is, the d-kernel of $(b_{n}^{g})_{n\geq 0}$ ) with the initial state being the whole sequence $(b_{n}^{g})_{n\geq 0}$ , and transition and output functions defined by Equation (4-1). Let $v\in X^{*}$ be an arbitrary vertex. By Corollary 5.6, the labels of the portrait of $(b_{n}^{g})_{n\geq 0}|_{v}$ at level $2$ and below coincide with the corresponding labels of the portrait of $(b_{n}^{g|_{v}})_{n\geq 0}$ . Therefore, each state $(b_{n}^{g})_{n\geq 0}|_{v}$ of $\mathcal B^{\prime }$ can be completely defined by a pair, called the label of this state:

(7-2) $$ \begin{align} l((b_{n}^{g})_{n\geq0}|_{v})=(g|_{v},(b^{g}_{\overline{vy}})_{y\in X}), \end{align} $$

where $(b^{g}_{\overline {vy}})_{y\in X}$ is the d-tuple of the first d terms of $(b_{n}^{g})_{n\geq 0}|_{v}$ that correspond to the labels of the first level of the portrait of this sequence. The first component of this pair defines the terms of $(b_{n}^{g|_{v}})_{n\geq 0}$ at level 2 and below, and the second component consists of terms of the first level. It is possible that different labels define the same state of $\mathcal B^{\prime }$ , but clearly the automaton $\mathcal B$ from the statement of the theorem also generates $(b_{n}^{g})_{n\geq 0}$ since its minimization coincides with $\mathcal B^{\prime }$ . Indeed, the set of states of $\mathcal B$ is the set of labels of states of $\mathcal B^{\prime }$ and the transitions in $\mathcal B$ are obtained from the transitions in $\mathcal B^{\prime }$ defined in Proposition 4.8, and the definition of labels.

Finally, the finiteness of $Q_{\mathcal B}$ follows from our proof of Theorem 1.1 since the set $\{g|_{v}\colon v\in X^{*}\}$ (coinciding with $Q_{\mathcal A}$ ) is finite, and the set $\{b^{g}_{\overline {vy}}\colon v\in X^{*}, y\in X\}$ is a subset of the finite set $\{b^{g^{\prime }}_{\overline {w}}\colon g^{\prime }\in Q_{\mathcal A}, w\in X\cup X^{2}\}$ .

For the algorithmic procedure that, given a finite state $g\in \mathop {\mathrm {End}}\nolimits (X^{*})$ , constructs a Moore automaton generating the sequence $(b^{g}_{n})_{n\geq 0}$ of its reduced van der Put coefficients, we need the following lemma.

Lemma 7.2. Given a finite state endomorphism $g\in G$ acting on $X^{*}$ with $|X|=d$ , its first $d^{2}$ reduced van der Put coefficients $b_{\overline {v}}^{g}$ , $v\in X^{*}$ of length at most $2$ , are eventually periodic elements of $\mathbb Z_{d}$ that can be algorithmically computed.

Proof. Suppose g has q states. If $\overline v=i<d$ , then by definition, $b_{i}^{g}=g(i0^{\infty })$ is the image of an eventually periodic word under a finite automaton transformation. Thus, it is also eventually periodic with the period of length at most q and the preperiod of length at most $q+1$ . Clearly, both the period and preperiod can be computed effectively. Further, if $d\leq \overline v<d^{2}$ , then $v=xy$ for $x,y\in X$ with $y\neq 0$ . In this case, $b^{g}_{\overline v}=({g(xy0^{\infty })-g(x0^{\infty })})/{d}$ is eventually periodic as a shifted difference of two eventually periodic words $g(xy0^{\infty })$ and $g(x0^{\infty })$ . The latter two words are eventually periodic as they are the images of eventually periodic words $xy0^{\infty }$ and $x0^{\infty }$ under a finite automaton transformation that can be effectively computed.

Algorithm 7.3 (construction of Moore automaton from Mealy automaton)

Suppose an endomorphism g of X ^* is defined by a finite state Mealy automaton A with the set of states Q _A. To construct a Moore automaton B defining the sequence of reduced van der Put coefficients , complete the following steps.

1. Step 1. Compute for each g′∈ Q _A and w ∈ X ∪ X ².

2. Step 2. Start building the set of states of B from its initial state with . Define Q ₀ = {q}.

3. Step 3. To build Q _i+1 from Q _i for i ≥ 1, start from the empty set and for each state and each x ∈ X, add the state to Q _i+1 unless it belongs to Q _j for some j ≤ i or is already in Q _i+1. Use Corollary 5.4 to identify with one of the elements computed in Step 1. Extend the transition function by δ(q, x) = q _x and the output function by .

4. Step 4. Repeat Step 3 until Q _i+1 = ∅.

5. Step 5. The set of states of the Moore automaton B is ⋃ _i≥0 Q _i , where the transition and output functions are defined in Step 3.

A particular connection between the constructed Moore automaton $\mathcal B$ and the original Mealy automaton $\mathcal A$ can be seen at the level of the underlying oriented graphs as explained below.

Definition 7.4. For a Mealy automaton $\mathcal A=(Q,X,\delta ,\lambda )$ , we define its underlying oriented graph $\Gamma (\mathcal A)$ to be the oriented labeled graph whose set of vertices is the set Q of states of $\mathcal A$ , and whose edges correspond to the transitions of $\mathcal A$ and are labeled by the input letters of the corresponding transitions. That is, there is an oriented edge from $q\in Q$ to $q^{\prime }\in Q$ labeled by $x\in X$ if and only if $\delta (q,x)=q^{\prime }$ .

In other words, the underlying oriented graph of a Mealy automaton $\mathcal A$ can be obtained from the Moore diagram of $\mathcal A$ by removing the second components of the edge labels. For example, Figure 6 depicts the underlying graph of a Mealy automaton from Figure 1 generating the lamplighter group $\mathcal L$ . Similarly, we construct underlying oriented graph of a Moore automaton.

Figure 6 Underlying graph for Mealy automaton from Figure 1 and Moore automaton from Figure 8.

Definition 7.5. For a Moore automaton $\mathcal B=(Q,X,\delta ,q_{0},A,\tau )$ , we define its underlying oriented graph $\Gamma (\mathcal B)$ to be the oriented labeled graph whose set of vertices is the set Q of states of $\mathcal B$ and whose edges correspond to the transitions of $\mathcal B$ and are labeled by the input letters of the corresponding transitions. That is, there is an oriented edge from $q\in Q$ to $q^{\prime }\in Q$ labeled by $x\in X$ if and only if $\delta (q,x)=q^{\prime }$ .

Figure 6 depicts also the underlying graph of a Moore automaton from Figure 8 generating the Thue–Morse sequence.

We finally define a covering of such oriented labeled graphs to be a surjective (both on vertices and edges) graph homomorphism that preserves the labels of the edges.

Corollary 7.6. Let $g\in \mathop {\mathrm {End}}\nolimits (X^{*})$ be an endomorphism of $X^{*}$ defined by a finite Mealy automaton $\mathcal A$ . Let also $(b_{n}^{g})_{n\geq 0}$ be the (automatic) sequence of the reduced van der Put coefficients of a transformation $\mathbb Z_{d}\to \mathbb Z_{d}$ induced by g. Then the underlying oriented graph $\Gamma (\mathcal B)$ of the Moore automaton $\mathcal B$ defining $(b_{n}^{g})_{n\geq 0}$ obtained from $\mathcal A$ by Algorithm 7.3 covers the underlying oriented graph $\Gamma (\mathcal A)$ .

Proof. Since the transitions in the original Mealy automaton $\mathcal A$ defining g are defined by $\delta (g|_{v},x)=g|_{vx}$ , we immediately get that the map from the set of vertices of the underlying oriented graph of $\mathcal B$ to the set of vertices of the underlying oriented graph of $\mathcal A$ defined by

$$ \begin{align*}(g|_{v},(b^{g}_{\overline{vy}})_{y\in X})\mapsto g|_{v}, v\in X^{*}\end{align*} $$

is a graph covering.

Now we describe the procedure that constructs a Mealy automaton of an endomorphism defined by an automatic sequence generated by a given Moore automaton.

Theorem 7.7. Let $g\in \mathop {\mathrm {End}}\nolimits (X^{*})$ be an endomorphism of $X^{*}$ induced by a transformation of $\mathbb Z_{d}$ for which the sequence of reduced van der Put coefficients $(b_{n}^{g})_{n\geq 0}\subset \mathbb Z_{d}$ is generated by a finite Moore automaton $\mathcal B$ with the set of states $Q_{\mathcal B}=\{(b_{n}^{g})_{n\geq 0}|_{v}\colon v\in X^{*}\}$ . Then the Mealy automaton $\mathcal A=(Q_{\mathcal A},X,\delta ,\lambda ,q)$ , where

• • the set of states is $Q_{\mathcal A}=\{((b^{g}_{n})_{n\geq 0}|_{v},(b^{g|_{v}}_{i})_{i=0,1,\ldots ,d-1})\colon v\in X^{*}\}$ ;

• • the transition and output functions are

  (7-3) $$ \begin{align} \begin{aligned} \delta(((b^{g}_{n})_{n\geq 0}|_{v},(b^{g|_{v}}_{i})_{i=0,1,\ldots,d-1}),x)&=((b^{g}_{n})_{n\geq 0}|_{vx},(b^{g|_{vx}}_{i})_{i=0,1,\ldots,d-1}),\\ \lambda(((b^{g}_{n})_{n\geq 0}|_{v},(b^{g|_{v}}_{i})_{i=0,1,\ldots,d-1}),x)&=b^{g|_{v}}_{\overline x}\,\mathrm{mod}\, d; \end{aligned} \end{align} $$

• • the initial state is $q=((b^{g}_{n})_{n\geq 0},(b^{g}_{i})_{i=0,1,\ldots ,d-1})$ ,

is finite, and defines the endomorphism g.

Proof. The initial Mealy automaton $\mathcal A^{\prime }$ defining g has set of states $Q^{\prime }=\{g|_{v}\colon v\in X^{*}\}$ , transition and output functions defined as

$$ \begin{align*} \begin{aligned} \delta^{\prime}(g|_{v},x)&=g|_{vx},\\ \lambda^{\prime}(g|_{v},x)&=g_{v}(x), \end{aligned} \end{align*} $$

and the initial state $g=g|_{\epsilon }$ .

Since each endomorphism of $X^{*}$ is uniquely defined by the sequence of its reduced van der Put coefficients, we can identify $Q^{\prime }$ with the set

$$ \begin{align*}\{(b^{g|_{v}}_{n})_{n\geq 0}\colon v\in X^{*}\}.\end{align*} $$

By Corollary 5.5, the sequence $(b^{g|_{v}}_{n})_{n\geq 0}$ of the reduced van der Put coefficients that defines $g|_{v}$ coincides starting from term d with $(b^{g}_{n})_{n\geq 0}|_{v}$ . Therefore, each state $g|_{v}$ of $\mathcal A^{\prime }$ can be completely defined by a pair, called the label of this state:

$$ \begin{align*} l(g|_{v})=((b^{g}_{n})_{n\geq 0}|_{v},(b^{g|_{v}}_{i})_{i=0,1,\ldots,d-1}), \end{align*} $$

where $(b^{g|_{v}}_{i})_{i=0,1,\ldots ,d-1}$ is the d-tuple of the first d terms of $(b_{n}^{g|_{v}})_{n\geq 0}$ that corresponds to the labels of the first level of the portrait of this sequence. As in (7-2), the first component of this pair defines the terms of $(b_{n}^{g|_{v}})_{n\geq 0}$ at level 2 and below, and the second component consists of terms of the first level.

Similarly to the case of Theorem 7.1, it is possible that different labels define the same state of $\mathcal A^{\prime }$ , but clearly the automaton $\mathcal A$ from the statement of the theorem also generates g since its minimization coincides with $\mathcal A^{\prime }$ . Indeed, the set of states of $\mathcal A$ is the set of labels of states of $\mathcal A^{\prime }$ and the transition and output functions in $\mathcal A$ are obtained from the corresponding functions in $\mathcal A^{\prime }$ and the definition of labels.

Finally, the finiteness of Q follows from the above proof of Theorem 1.1 since the set $\{(b^{g}_{n})_{n\geq 0}|_{v}\colon v\in X^{*}\}$ (coinciding with $Q_{\mathcal B}$ ) is finite, and the set $\{b^{g|_{v}}_{i}\colon v\in X^{*}, i=0,1,\ldots ,d-1\}$ is finite as well, which follows from Lemma 6.3.

We conclude with the description of the algorithm for building the Mealy automaton of an endomorphism of $X^{*}$ from a Moore automaton defining the sequence of its reduced van der Put coefficients.

Algorithm 7.8 (construction of Mealy automaton from Moore automaton)

Let g ∈\,End(X ^*) be an endomorphism of X ^* induced by a transformation of ℤ _d for which the sequence of reduced van der Put coefficients (b _n ^g ) _n≥0, b _n ^g ∈ ℤ _d is defined by a finite Moore automaton B with the set of states Q _B = {(b _n ^g ) _n≥0| _v : v ∈ X ^*}. To construct a Mealy automaton A = (Q, X, δ, λ, q) defining endomorphism g, complete the following steps.

1. Step 1. Start building the set of states of A from its initial state with τ(q) = b ₀ ^g . Define Q ₀ = {q}.

2. Step 2. To build Q _i+1 from Q _i for i ≥ 1, start from the empty set and for each state and each x ∈ X, add state q _x = ((b _n ^g ) _n≥0| _vx , (b _i ^{g| _vx} ) _{i=0, 1, …, d−1}) to Q _i+1 unless it belongs to Q _j for some j ≤ i or is already in Q _i+1. Use the second case in Equation (5-1) to calculate b _i ^{g| _vx} from the coefficients b _j ^g , which are the values of the output function of the given Moore automaton. Extend the transition function by δ(q, x) = q _x and the output function by λ(q, x) = b _x¯ ^{g| _v} mod d.

3. Step 3. Repeat Step 2 until Q _i+1 = ∅.

4. Step 4. The set of states of Mealy automaton A is ⋃ _i≥0 Q _i , where the transition and output functions are defined in Step 2.

Corollary 7.9. Let $g\in \mathop {\mathrm {End}}\nolimits (X^{*})$ be an endomorphism of $X^{*}$ induced by a selfmap of $\mathbb Z_{d}$ with the sequence of reduced van der Put coefficients defined by finite Moore automaton $\mathcal B$ . Then the underlying oriented graph $\Gamma (\mathcal A)$ of the Mealy automaton $\mathcal A$ obtained from $\mathcal B$ by Algorithm 7.8 covers the underlying oriented graph of $\mathcal B$ .

Proof. Since the transitions in the original Moore automaton $\mathcal B$ defining g are defined by $\delta ((b^{g}_{n})_{n\geq 0}|_{v},x)=(b^{g}_{n})_{n\geq 0}|_{vx}$ , we immediately get that the map from the underlying oriented graph of $\mathcal A$ to the underlying oriented graph of $\mathcal B$ defined by

$$ \begin{align*}((b^{g}_{n})_{n\geq 0}|_{v},(b^{g|_{v}}_{i})_{i=0,1,\ldots,d-1})\mapsto (b^{g}_{n})_{n\geq 0}|_{v}, v\in X^{*}\end{align*} $$

is a graph covering.

8 Examples

8.1 Moore automaton from Mealy automaton

We first give an example of the construction of a Moore automaton from Mealy automaton. Consider the lamplighter group $\mathcal L=(\mathbb Z/2\mathbb Z)\wr \mathbb Z$ generated by the 2-state Mealy automaton $\mathcal A$ over the 2-letter alphabet $X=\{0,1\}$ from [24] shown in Figure 1 and defined by the following wreath recursion:

$$ \begin{align*}\begin{aligned} p&=(p,q)(01),\\ q&=(p,q). \end{aligned} \end{align*} $$

Proposition 8.1. The Moore automaton $\mathcal B_{p}$ generating the sequence of reduced van der Put coefficients of the transformation of $\mathbb Z_{2}$ induced by automorphism p is shown in Figure 7, where the initial state is on top, and the value of the output function $\tau $ of $\mathcal B_{p}$ at a given state is equal to the first component of the pair of d-adic integers in its label.

Proof. We apply Algorithm 7.3 and construct the sections of $(b^{p}_{n})_{n\geq 0}$ at the vertices of $X^{*}$ in the form of (7-1). It may be useful to refer to Figure 7 to understand better the calculations that follow.

Figure 7 Moore automaton $\mathcal B_{p}$ generating the sequence $(b^{p}_{n})_{n\geq 0}$ of reduced van der Put coefficients of the generator p of the lamplighter group $\mathcal L$ .

The label of the initial state $(b^{p}_{n})_{n\geq 0}|_{\varepsilon }$ of $\mathcal B_{p}$ is $(p|_{\varepsilon },(b^{p}_{0},b^{p}_{1}))$ . By (3-4), we get:

$$ \begin{align*}b^{p}_{0}=p(0^{\infty})=1^{\infty}\quad\text{and}\quad {b}^{p}_{1}=p(10^{\infty})=001^{\infty}.\end{align*} $$

Therefore, the initial state of $\mathcal B_{p}$ is labeled by

$$ \begin{align*}l((b^{p}_{n})_{n\geq0}|_{\varepsilon})=(p,(1^{\infty},001^{\infty})).\end{align*} $$

We proceed with the states corresponding to the vertices of the first level of $X^{*}$ . We calculate:

$$ \begin{align*}b^{p}_{2}=\frac{p(010^{\infty})-p(0^{\infty})}2=\frac{1001^{\infty}-1^{\infty}}2=101^{\infty},\end{align*} $$

$$ \begin{align*}b^{p}_{3}=\frac{p(110^{\infty})-p(10^{\infty})}2=\frac{0101^{\infty}-001^{\infty}}2=1^{\infty}.\end{align*} $$

Therefore, we get the labels of two more states in $\mathcal B_{p}$ :

$$ \begin{align*}l((b^{p}_{n})_{n\geq0}|_{0})=(p|_{0},(b^{p}_{0},b^{p}_{2}))=(p,(1^{\infty},101^{\infty})),\end{align*} $$

$$ \begin{align*}l((b^{p}_{n})_{n\geq0}|_{1})=(p|_{1},(b^{p}_{1},b^{p}_{3}))=(q,(001^{\infty},1^{\infty})).\end{align*} $$

To obtain labels of the states at the vertices of deeper levels, we use Corollary 5.4. Namely, for $n>3$ , we have that $[n]_{2}=vx1\in X^{*}$ for some $v\in X^{*}$ and $x\in X$ . Therefore, by Corollary 5.4,

$$ \begin{align*}b^{p}_{n}=b^{p}_{\overline{vx1}}=b^{p|_{v}}_{\overline{x1}}=b^{p|_{v}}_{n\,\mathrm{mod}\, 4}.\end{align*} $$

Therefore, it is enough to compute the first four values of $(b^{p|_{v}}_{n})_{n\geq 0}$ for all states $p|_{v}$ of an automaton $\mathcal A$ . Since there are only two states in $\mathcal A$ and we have computed the first four values of $(b^{p}_{n})_{n\geq 0}$ , we proceed to $(b^{p}_{n})_{n\geq 0}$ :

$$ \begin{align*}\begin{aligned} b^{q}_{0}&=q(0^{\infty})=01^{\infty},\\ b^{q}_{1}&=q(10^{\infty})=101^{\infty},\\ b^{q}_{2}&=\frac{q(010^{\infty})-q(0^{\infty})}2=\frac{0001^{\infty}-01^{\infty}}2=101^{\infty},\\ b^{q}_{3}&=\frac{q(110^{\infty})-q(10^{\infty})}2=\frac{1101^{\infty}-101^{\infty}}2=1^{\infty}. \end{aligned} \end{align*} $$

Now, by Corollary 5.5, we have that

$$ \begin{align*}\begin{aligned} b^{p}_{4}&=b^{p}_{\overline{001}}=b^{p|_{0}}_{\overline{01}}=b^{p}_{\overline{01}}=b^{p}_{2}=101^{\infty},\\ b^{p}_{6}&=b^{p}_{\overline{011}}=b^{p|_{0}}_{\overline{11}}=b^{p}_{\overline{11}}=b^{p}_{3}=1^{\infty},\\ b^{p}_{5}&=b^{p}_{\overline{101}}=b^{p|_{1}}_{\overline{01}}=b^{q}_{\overline{01}}=b^{q}_{2}=101^{\infty},\\ b^{p}_{7}&=b^{p}_{\overline{111}}=b^{p|_{1}}_{\overline{11}}=b^{q}_{\overline{11}}=b^{q}_{3}=1^{\infty}. \end{aligned} \end{align*} $$

Thus, the states at the second level have the following labels:

$$ \begin{align*}\begin{aligned} l((b^{p}_{n})_{n\geq0}|_{00})&=(p|_{00},(b^{p}_{\overline{000}},b^{p}_{\overline{001}}))=(p,(b^{p}_{0},b^{p}_{4}))=(p,(1^{\infty},101^{\infty})),\\ l((b^{p}_{n})_{n\geq0}|_{01})&=(p|_{01},(b^{p}_{\overline{010}},b^{p}_{\overline{011}}))=(q,(b^{p}_{2},b^{p}_{6}))=(q,(101^{\infty},1^{\infty})),\\ l((b^{p}_{n})_{n\geq0}|_{10})&=(p|_{10},(b^{p}_{\overline{100}},b^{p}_{\overline{101}}))=(p,(b^{p}_{1},b^{p}_{5}))=(p,(001^{\infty},101^{\infty})),\\ l((b^{p}_{n})_{n\geq0}|_{11})&=(p|_{11},(b^{p}_{\overline{110}},b^{p}_{\overline{111}}))=(q,(b^{p}_{3},b^{p}_{7}))=(q,(1^{\infty},1^{\infty})).\\ \end{aligned} \end{align*} $$

Since $l((b^{p}_{n})_{n\geq 0}|_{00})=l((b^{p}_{n})_{n\geq 0}|_{0})$ , we can stop calculations along this branch. For other branches, we compute similarly on the next level. We start from branch $01$ :

$$ \begin{align*}l((b^{p}_{n})_{n\geq0}|_{010})=(p|_{010},(b^{p}_{\overline{0100}},b^{p}_{\overline{0101}}))=(p,(b^{p}_{2},b^{p|_{01}}_{\overline{01}}))=(p,(b^{p}_{2},b^{q}_{2}))=(p,(101^{\infty},101^{\infty})),\end{align*} $$

and

$$ \begin{align*} l((b^{p}_{n})_{n\geq0}|_{011})&=(p|_{011},(b^{p}_{\overline{0110}},b^{p}_{\overline{0111}}))=(q,(b^{p|_{0}}_{\overline{11}},b^{p|_{01}}_{\overline{11}}))\\ &=(q,(b^{p}_{3},b^{q}_{3}))=(q,(1^{\infty},1^{\infty}))=l((b^{p}_{n})_{n\geq0}|_{11}).\\ \end{align*} $$

For branch $10$ , we obtain

$$ \begin{align*} l((b^{p}_{n})_{n\geq0}|_{100})&=(p|_{100},(b^{p}_{\overline{1000}},b^{p}_{\overline{1001}}))=(p,(b^{p}_{1},b^{p|_{10}}_{\overline{01}}))\\ &=(p,(b^{p}_{1},b^{p}_{2}))=(p,(001^{\infty},101^{\infty}))=l((b^{p}_{n})_{n\geq0}|_{10}) \end{align*} $$

and

$$ \begin{align*} l((b^{p}_{n})_{n\geq0}|_{101})=(p|_{101},(b^{p}_{\overline{1010}},b^{p}_{\overline{1011}}))=(q,(b^{p|_{1}}_{\overline{01}},b^{p|_{10}}_{\overline{11}}))=(q,(b^{q}_{2},b^{p}_{2}))=(q,(101^{\infty},101^{\infty})). \end{align*} $$

For branch $11$ , we get

$$ \begin{align*} l((b^{p}_{n})_{n\geq0}|_{110})&=(p|_{110},(b^{p}_{\overline{1100}},b^{p}_{\overline{1101}}))=(p,(b^{p}_{3},b^{p|_{11}}_{\overline{01}}))\\ &=(p,(b^{p}_{3},b^{q}_{2}))=(p,(1^{\infty},101^{\infty}))=l((b^{p}_{n})_{n\geq0}|_{0}) \end{align*} $$

and

$$ \begin{align*} l((b^{p}_{n})_{n\geq0}|_{111})&=(p|_{111},(b^{p}_{\overline{1110}},b^{p}_{\overline{1111}}))=(q,(b^{p|_{1}}_{\overline{11}},b^{p|_{11}}_{\overline{11}}))\\ &=(q,(b^{q}_{3},b^{q}_{3}))=(q,(1^{\infty},1^{\infty}))=l((b^{p}_{n})_{n\geq0}|_{11}). \end{align*} $$

At this moment, we have two unfinished branches: $010$ and $101$ . For $010$ , we have

$$ \begin{align*} l((b^{p}_{n})_{n\geq0}|_{0100})&=(p|_{0100},(b^{p}_{\overline{01000}},b^{p}_{\overline{01001}}))=(p,(b^{p}_{2},b^{p|_{010}}_{\overline{01}}))\\ &=(p,(b^{p}_{2},b^{p}_{2}))=(p,(101^{\infty},101^{\infty}))=l((b^{p}_{n})_{n\geq0}|_{010}) \end{align*} $$

and

$$ \begin{align*} l((b^{p}_{n})_{n\geq0}|_{0101})&=(p|_{0101},(b^{p}_{\overline{01010}},b^{p}_{\overline{01011}}))=(q,(b^{p|_{01}}_{\overline{01}},b^{p|_{010}}_{\overline{11}}))\\ &=(q,(b^{q}_{2},b^{p}_{3}))=(q,(101^{\infty},1^{\infty}))=l((b^{p}_{n})_{n\geq0}|_{01}). \end{align*} $$

Finally, for branch $101$ , we compute

$$ \begin{align*} l((b^{p}_{n})_{n\geq0}|_{1010})&=(p|_{1010},(b^{p}_{\overline{10100}},b^{p}_{\overline{10101}}))=(p,(b^{p|_{1}}_{\overline{01}},b^{p|_{101}}_{\overline{01}}))\\ &=(p,(b^{q}_{2},b^{q}_{2}))=(p,(101^{\infty},101^{\infty}))=l((b^{p}_{n})_{n\geq0}|_{010}) \end{align*} $$

and

$$ \begin{align*} l((b^{p}_{n})_{n\geq0}|_{1011})&=(p|_{1011},(b^{p}_{\overline{10110}},b^{p}_{\overline{10111}}))=(q,(b^{p|_{10}}_{\overline{11}},b^{p|_{101}}_{\overline{11}}))\\ &=(q,(b^{p}_{3},b^{q}_{3}))=(q,(1^{\infty},1^{\infty}))=l((b^{p}_{n})_{n\geq0}|_{11}). \end{align*} $$

We have completed all the branches and constructed all the transitions in the automaton $\mathcal B_{p}$ .

8.2 Mealy automaton from Moore automaton

In this subsection, we provide an example of the converse construction. Namely, we construct the finite state endomorphism of $\{0,1\}^{*}$ that induces a transformation of $\mathbb Z_{2}$ with the Thue–Morse sequence of reduced van der Put coefficients, where we treat $0$ as $0^{\infty }$ and $1$ as $10^{\infty }$ according to the standard embedding of $\mathbb Z$ into $\mathbb Z_{2}$ .

Recall that the Thue–Morse sequence $(t_{n})_{n\geq 0}$ is the binary sequence defined by a Moore automaton shown in Figure 8. It can be obtained by starting with 0 and successively appending the Boolean complement of the sequence obtained thus far. The first 32 values of this sequence are shown in Table 1.

Table 1 First 32 values of the Thue–Morse sequence.

Figure 8 Moore automaton $\mathcal B$ generating the Thue–Morse sequence.

Proposition 8.2. The endomorphism t of $X^{*}$ inducing a transformation of $\mathbb Z_{2}$ with the Thue–Morse sequence $(b^{t}_{n})_{n\geq 0}=(t_{n})_{n\geq 0}$ of the reduced van der Put coefficients is defined by the $2$ -state Mealy automaton $\mathcal A_{t}$ shown in Figure 9 with the following wreath recursion:

$$ \begin{align*}\begin{aligned} t&=(t,s),\\ s&=(s,t) {{0 1}\choose{0 0}}, \end{aligned}\end{align*} $$

where ${{0 1}\choose {0 0}}$ denotes the selfmap of $\{0,1\}$ sending both of its elements to $0$ .

Figure 9 Mealy automaton $\mathcal A_{t}$ defining a transformation of $\mathbb Z_{2}$ whose sequence of reduced van der Put coefficients is the Thue–Morse sequence.

Proof. We follow Algorithm 7.8, according to which the states of $\mathcal A_{t}$ are the pairs of the form

$$ \begin{align*} l(t|_{v})=((b^{t}_{n})_{n\geq 0}|_{v},(b^{t|_{v}}_{0}, b^{t|_{v}}_{1})). \end{align*} $$

Below we suppress the subscript $n\geq 0$ in the notation for sequences to simplify the exposition. For example, we write simply $(b^{t}_{n})$ for $(b^{t}_{n})_{n\geq 0}$ .

The initial state t has a label

$$ \begin{align*}l(t)=l(t|_{\varepsilon})=((b^{t}_{n}),(b^{t}_{0}, b^{t}_{1}))=((b^{t}_{n}),(0^{\infty}, 10^{\infty})).\end{align*} $$

We proceed to calculate the labels of the sections at the vertices of the first level. Using Theorem 5.1 (namely, the first two cases in Equation (5-1)) and the values $b^{t}_{n}=t_{n}$ of the Thue–Morse sequence from Table 1, we obtain:

$$ \begin{align*} l(t|_{0})&=((b^{t}_{n})|_{0},(b^{t|_{0}}_{0}, b^{t|_{0}}_{1}))=((b^{t}_{n}),(\sigma(b^{t}_{0}), b^{t}_{2}+\sigma(b^{t}_{0})))\\ &=((b^{t}_{n}),(\sigma(0^{\infty}), 10^{\infty}+\sigma(0^{\infty})))=((b^{t}_{n}),(0^{\infty}, 10^{\infty}))=l(t). \end{align*} $$

We also use above the fact that $(b^{t}_{n})|_{0}=(b^{t}_{n})$ , which follows from the structure of automaton $\mathcal B$ . Therefore, we can stop developing the branch that starts with 0 and move to the branch starting from 1. Similarly, we get

(8-1) $$ \begin{align} l(t|_{1})&=((b^{t}_{n})|_{1},(b^{t|_{1}}_{0}, b^{t|_{1}}_{1}))=((b^{t}_{n})|_{1},(\sigma(b^{t}_{1}), b^{t}_{3}+\sigma(b^{t}_{1})))\nonumber\\ &=((b^{t}_{n})|_{1},(\sigma(10^{\infty}), 0^{\infty}+\sigma(10^{\infty})))=((b^{t}_{n})|_{1},(0^{\infty}, 0^{\infty})), \end{align} $$

so we obtain a new section. We compute the sections at the vertices of the second level using Figure 5, keeping in mind that according to Equation (8-1), $b^{t|_{1}}_{0}=0^{\infty }$ :

$$ \begin{align*} l(t|_{10})&=((b^{t}_{n})|_{10},(b^{t|_{10}}_{0}, b^{t|_{10}}_{1}))=((b^{t}_{n})|_{1},(b^{(t|_{1})|_{0}}_{0}, b^{(t|_{1})|_{0}}_{1}))\\ &=((b^{t}_{n})|_{1},(\sigma(b^{t|_{1}}_{0}), b^{t|_{1}}_{2}+\sigma(b^{t|_{1}}_{0})))=((b^{t}_{n})|_{1},(\sigma(0^{\infty}), b^{t}_{5}+\sigma(0^{\infty})))\\ &=((b^{t}_{n})|_{1},(0^{\infty}, 0^{\infty}+0^{\infty}))=((b^{t}_{n})|_{1},(0^{\infty}, 0^{\infty}))=l(t|_{1}). \end{align*} $$

Finally, since according to Equation (8-1) $b^{t|_{1}}_{1}=0^{\infty }$ , we calculate the last section at $11$ :

$$ \begin{align*} l(t|_{11})&=((b^{t}_{n})|_{11},(b^{t|_{11}}_{0}, b^{t|_{11}}_{1}))=((b^{t}_{n}),(b^{(t|_{1})|_{1}}_{0}, b^{(t|_{1})|_{1}}_{1}))\\ &=((b^{t}_{n}),(\sigma(b^{t|_{1}}_{1}), b^{t|_{1}}_{3}+\sigma(b^{t|_{1}}_{1})))=((b^{t}_{n}),(\sigma(0^{\infty}), b^{t}_{7}+\sigma(0^{\infty})))\\ &=((b^{t}_{n}),(0^{\infty}, 10^{\infty}+0^{\infty}))=((b^{t}_{n}),(0^{\infty}, 10^{\infty}))=l(t). \end{align*} $$

We have completed all the branches and constructed all the transitions in the automaton $\mathcal A_{t}$ . We only need now to compute the values of the output function. By Equation (7-3), we get

$$ \begin{align*} \begin{aligned} \lambda(((b^{t}_{n}),(0^{\infty},10^{\infty})),0)&=0^{\infty}\,\mathrm{mod}\, 2=0,\\ \lambda(((b^{t}_{n}),(0^{\infty},10^{\infty})),1)&=10^{\infty}\,\mathrm{mod}\, 2=1,\\ \lambda(((b^{t}_{n})|_{1},(0^{\infty},0^{\infty})),0)&=0^{\infty}\,\mathrm{mod}\, 2=0,\\ \lambda(((b^{t}_{n})|_{1},(0^{\infty},0^{\infty})),1)&=0^{\infty}\,\mathrm{mod}\, 2=0, \end{aligned} \end{align*} $$

which completes the proof of the proposition.