 $\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRAS
$\boldsymbol {\mathcal {O}}$ FOR LIE SUPERALGEBRASPublished online by Cambridge University Press: 21 January 2022
For classical Lie superalgebras of type I, we provide necessary and sufficient conditions for a Verma supermodule
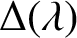 $\Delta (\lambda )$
to be such that every nonzero homomorphism from another Verma supermodule to
$\Delta (\lambda )$
to be such that every nonzero homomorphism from another Verma supermodule to
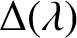 $\Delta (\lambda )$
is injective. This is applied to describe the socle of the cokernel of an inclusion of Verma supermodules over the periplectic Lie superalgebras
$\Delta (\lambda )$
is injective. This is applied to describe the socle of the cokernel of an inclusion of Verma supermodules over the periplectic Lie superalgebras
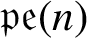 $\mathfrak {pe} (n)$
and, furthermore, to reduce the problem of description of
$\mathfrak {pe} (n)$
and, furthermore, to reduce the problem of description of
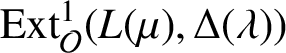 $\mathrm {Ext}^1_{\mathcal O}(L(\mu ),\Delta (\lambda ))$
for
$\mathrm {Ext}^1_{\mathcal O}(L(\mu ),\Delta (\lambda ))$
for
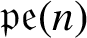 $\mathfrak {pe} (n)$
to the similar problem for the Lie algebra
$\mathfrak {pe} (n)$
to the similar problem for the Lie algebra
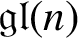 $\mathfrak {gl}(n)$
. Additionally, we study the projective and injective dimensions of structural supermodules in parabolic category
$\mathfrak {gl}(n)$
. Additionally, we study the projective and injective dimensions of structural supermodules in parabolic category
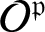 $\mathcal O^{\mathfrak {p}}$
for classical Lie superalgebras. In particular, we completely determine these dimensions for structural supermodules over the periplectic Lie superalgebra
$\mathcal O^{\mathfrak {p}}$
for classical Lie superalgebras. In particular, we completely determine these dimensions for structural supermodules over the periplectic Lie superalgebra
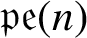 $\mathfrak {pe} (n)$
and the orthosymplectic Lie superalgebra
$\mathfrak {pe} (n)$
and the orthosymplectic Lie superalgebra
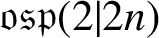 $\mathfrak {osp}(2|2n)$
.
$\mathfrak {osp}(2|2n)$
.
Communicated by Anthony Henderson
The first author is partially supported by MoST grant 108-2115-M-008-018-MY2. For the second author, the research was partially supported by the Swedish Research Council and Göran Gustafssons Stiftelse.