SOME ISOMORPHISMS IN DERIVED FUNCTORS AND THEIR APPLICATIONS

Abstract

Let 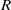$R$ be a commutative Noetherian ring, 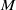$M$ be a finitely generated 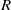$R$-module and $\mathfrak{a}$ be an ideal of 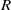$R$ such that 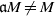$\mathfrak{a}M\not = M$. We show among the other things that, if $c$ is a nonnegative integer such that 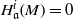${ H}_{\mathfrak{a}}^{i} (M)= 0$ for all 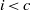$i\lt c$, then there is an isomorphism 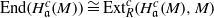$\mathrm{End} ({ H}_{\mathfrak{a}}^{c} (M))\cong { \mathrm{Ext} }_{R}^{c} ({ H}_{\mathfrak{a}}^{c} (M), M)$; and if $c$ is a nonnegative integer such that 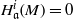${ H}_{\mathfrak{a}}^{i} (M)= 0$ for all 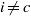$i\not = c$, there are the following isomorphisms:

(i) 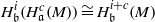$~\quad{ H}_{\mathfrak{b}}^{i} ({ H}_{\mathfrak{a}}^{c} (M))\cong { H}_{\mathfrak{b}}^{i+ c} (M)$ and

(ii) 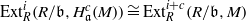$\quad{ \mathrm{Ext} }_{R}^{i} (R/ \mathfrak{b}, { H}_{\mathfrak{a}}^{c} (M))\cong { \mathrm{Ext} }_{R}^{i+ c} (R/ \mathfrak{b}, M)$

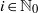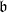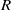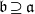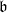for all $i\in { \mathbb{N} }_{0} $ and all ideals $\mathfrak{b}$ of $R$ with $\mathfrak{b}\supseteq \mathfrak{a}$. We also prove that if $\mathfrak{a}$ and $\mathfrak{b}$ are ideals of 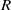$R$ with 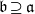$\mathfrak{b}\supseteq \mathfrak{a}$ and 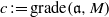$c: = \mathrm{grade} (\mathfrak{a}, M)$, then there exists a natural homomorphism from 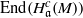$\mathrm{End} ({ H}_{\mathfrak{a}}^{c} (M))$ to 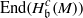$\mathrm{End} ({ H}_{\mathfrak{b}}^{c} (M))$, where 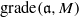$\mathrm{grade} (\mathfrak{a}, M)$ is the maximum length of 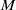$M$-sequences in $\mathfrak{a}$.