Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T23:57:16.925Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME REFINED RESULTS ON THE MIXED LITTLEWOOD CONJECTURE FOR PSEUDO-ABSOLUTE VALUES

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  22 August 2018

WENCAI LIU
WENCAI LIU*
Affiliation:
Department of Mathematics, University of California Irvine, California 92697-3875, USA email liuwencai1226@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the mixed Littlewood conjecture with pseudo-absolute values. For any pseudo-absolute-value sequence 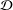${\mathcal{D}}$, we obtain a sharp criterion such that for almost every $\unicode[STIX]{x1D6FC}$ the inequality

$$\begin{eqnarray}|n|_{{\mathcal{D}}}|n\unicode[STIX]{x1D6FC}-p|\leq \unicode[STIX]{x1D713}(n)\end{eqnarray}$$
has infinitely many coprime solutions $(n,p)\in \mathbb{N}\times \mathbb{Z}$ for a certain one-parameter family of 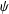$\unicode[STIX]{x1D713}$. Also, under a minor condition on pseudo-absolute-value sequences 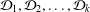${\mathcal{D}}_{1},{\mathcal{D}}_{2},\ldots ,{\mathcal{D}}_{k}$, we obtain a sharp criterion on a general sequence 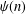$\unicode[STIX]{x1D713}(n)$ such that for almost every $\unicode[STIX]{x1D6FC}$ the inequality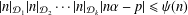
$$\begin{eqnarray}|n|_{{\mathcal{D}}_{1}}|n|_{{\mathcal{D}}_{2}}\cdots |n|_{{\mathcal{D}}_{k}}|n\unicode[STIX]{x1D6FC}-p|\leq \unicode[STIX]{x1D713}(n)\end{eqnarray}$$
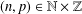 has infinitely many coprime solutions $(n,p)\in \mathbb{N}\times \mathbb{Z}$.

Keywords

Littlewood conjecturepseudo-absolute valuesdiophantine approximation

MSC classification

Primary: 11K60: Diophantine approximation
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 107 , Issue 1 , August 2019 , pp. 91 - 109
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The author was supported by the AMS-Simons Travel Grant 2016–2018 and NSF DMS-1700314. This research was also partially supported by NSF DMS-1401204.

References

Badziahin, D. A., ‘On multiplicatively badly approximable numbers’, Mathematika 59(1) (2013), 31–55.Google Scholar
Beresnevich, V., Harman, G., Haynes, A. and Velani, S., ‘The Duffin–Schaeffer conjecture with extra divergence II’, Math. Z. 275(1–2) (2013), 127–133.Google Scholar
Bourgain, J., Lindenstrauss, E., Michel, P. and Venkatesh, A., ‘Some effective results for × a × b ’, Ergodic Theory Dynam. Systems 29(6) (2009), 1705–1722.Google Scholar
Bugeaud, Y., ‘Around the Littlewood conjecture in Diophantine approximation’, Publ. Math. Besançon 2014(1) (2014), 5–18.Google Scholar
Bugeaud, Y., Haynes, A. and Velani, S., ‘Metric considerations concerning the mixed Littlewood conjecture’, Int. J. Number Theory 7(3) (2011), 593–609.Google Scholar
Bugeaud, Y. and Moshchevitin, N., ‘Badly approximable numbers and Littlewood-type problems’, Math. Proc. Cambridge Philos. Soc. 150 (2011), 215–226.Google Scholar
de Mathan, B. and Teulié, O., ‘Problemes diophantiens simultanés’, Monatsh. Math. 143(3) (2004), 229–245.Google Scholar
Duffin, R. J. and Schaeffer, A. C., ‘Khintchine’s problem in metric Diophantine approximation’, Duke Math. J. 8(2) (1941), 243–255.Google Scholar
Einsiedler, M., Katok, A. and Lindenstrauss, E., ‘Invariant measures and the set of exceptions to Littlewood’s conjecture’, Ann. of Math. (2) 164 (2006), 513–560.Google Scholar
Einsiedler, M. and Kleinbock, D., ‘Measure rigidity and p-adic Littlewood-type problems’, Compos. Math. 143(3) (2007), 689–702.Google Scholar
Furstenberg, H., ‘Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation’, Math. Syst. Theory 1 (1967), 1–49.Google Scholar
Gallagher, P., ‘Approximation by reduced fractions’, J. Math. Soc. Japan 13 (1961), 342–345.Google Scholar
Gallagher, P., ‘Metric simultaneous diophantine approximation’, J. Lond. Math. Soc. 37 (1962), 387–390.Google Scholar
Harrap, S. and Haynes, A., ‘The mixed Littlewood conjecture for pseudo-absolute values’, Math. Ann. 357(3) (2013), 941–960.Google Scholar
Haynes, A. K., Pollington, A. D. and Velani, S. L., ‘The Duffin–Schaeffer conjecture with extra divergence’, Math. Ann. 353(2) (2012), 259–273.Google Scholar
Li, L., ‘A note on the Duffin–Schaeffer conjecture’, Unif. Distrib. Theory 8(2) (2013), 151–156.Google Scholar
Li, L., ‘The Duffin–Schaeffer-type conjectures in various local fields’, Mathematika 62(3) (2016), 753–800.Google Scholar
Peres, Y. and Schlag, W., ‘Two Erdős problems on lacunary sequences: chromatic number and Diophantine approximation’, Bull. Lond. Math. Soc. 42(2) (2010), 295–300.Google Scholar
Pollington, A. D. and Vaughan, R. C., ‘The k-dimensional Duffin and Schaeffer conjecture’, Mathematika 37(2) (1990), 190–200.Google Scholar
Strauch, O., ‘Duffin–Schaeffer conjecture and some new types of real sequences’, Acta Math. Univ. Comenian. (N.S.) 40–41 (1982), 233–265.Google Scholar