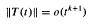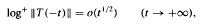Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Galé, José E.
and
Miana, Pedro J.
2006.
One-parameter groups of regular quasimultipliers.
Journal of Functional Analysis,
Vol. 237,
Issue. 1,
p.
1.
Mustafayev, Heybetkulu
2021.
Local spectrum, local spectral radius, and growth conditions.
Monatshefte für Mathematik,
Vol. 195,
Issue. 4,
p.
717.