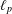Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2016.
Mean ergodicity and spectrum of the Cesàro operator on weighted $$c_0$$ c 0 spaces.
Positivity,
Vol. 20,
Issue. 4,
p.
761.
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2018.
The Cesàro operator in weighted ℓ1 spaces.
Mathematische Nachrichten,
Vol. 291,
Issue. 7,
p.
1015.
Abadias, Luciano
and
Miana, Pedro J.
2018.
Generalized Cesàro operators, fractional finite differences and Gamma functions.
Journal of Functional Analysis,
Vol. 274,
Issue. 5,
p.
1424.
PEDERSEN, THOMAS VILS
2019.
GENERALIZED HARDY–CESÀRO OPERATORS BETWEEN WEIGHTED SPACES.
Glasgow Mathematical Journal,
Vol. 61,
Issue. 1,
p.
13.
Bonet, José
and
Ricker, Werner J.
2020.
Order spectrum of the Cesàro operator in Banach lattice sequence spaces.
Positivity,
Vol. 24,
Issue. 3,
p.
593.
Sawano, Yoshihiro
and
El-Shabrawy, Saad R.
2020.
Fine spectra of the discrete generalized Cesàro operator on Banach sequence spaces.
Monatshefte für Mathematik,
Vol. 192,
Issue. 1,
p.
185.
El-Shabrawy, Saad R.
2021.
On q−Cesàro Operators: Boundedness, Compactness and Spectra.
Numerical Functional Analysis and Optimization,
Vol. 42,
Issue. 9,
p.
1019.
Curbera, Guillermo P.
and
Ricker, Werner J.
2022.
Fine spectra and compactness of generalized Cesàro operators in Banach lattices in CN0.
Journal of Mathematical Analysis and Applications,
Vol. 507,
Issue. 2,
p.
125824.
El-Shabrawy, Saad
2022.
Compactness criteria and spectra of some infinite lower triangular matrices.
Filomat,
Vol. 36,
Issue. 17,
p.
5913.
Patra, Arnab
Rani, Jyoti
and
Kumar Mahto, Sanjay
2023.
Spectral properties of the Rhaly operator on weighted null sequence spaces and associated operator ideals.
Asian-European Journal of Mathematics,
Vol. 16,
Issue. 10,
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2023.
Spectral properties of generalized Cesàro operators in sequence spaces.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 117,
Issue. 4,
Akhymbek, Meiram
Tulenov, Kanat
and
Zaur, Gulnur
2024.
Spectrum of the Cesàro-Hardy operator in rearrangement invariant spaces.
Quaestiones Mathematicae,
Vol. 47,
Issue. 6,
p.
1157.
Abanin, A. V.
and
Mannanikov, R. S.
2024.
Weighted Composition Operators on Quasi-Banach Weighted Sequence Spaces.
Siberian Mathematical Journal,
Vol. 65,
Issue. 4,
p.
909.
Albanese, Angela A.
Bonet, José
and
Ricker, Werner J.
2025.
Mean ergodic and related properties of generalized Cesàro operators in BK-sequence spaces.
Monatshefte für Mathematik,
Vol. 206,
Issue. 1,
p.
1.