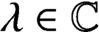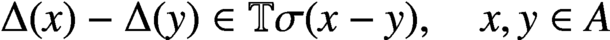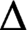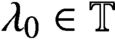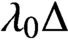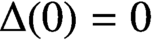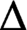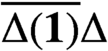Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jiménez-Vargas, Antonio
and
Ramírez, María Isabel
2021.
Algebraic Reflexivity of Non-Canonical Isometries on Lipschitz Spaces.
Mathematics,
Vol. 9,
Issue. 14,
p.
1635.
Moslehian, M. S.
Muñoz-Fernández, G. A.
Peralta, A. M.
and
Seoane-Sepúlveda, J. B.
2022.
Similarities and differences between real and complex Banach spaces: an overview and recent developments.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 116,
Issue. 2,
Gyenti, Bálint
2022.
On 2-local automorphisms of symmetric groups.
European Journal of Mathematics,
Vol. 8,
Issue. S1,
p.
290.
Hosseini, Maliheh
Jiménez-Vargas, A.
and
Ramírez, María Isabel
2022.
On local isometries between algebras of C(Y)-valued differentiable maps.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 116,
Issue. 3,
Font, Juan J.
and
Hosseini, Maliheh
2023.
Local Isometries on Subspaces of Continuous Functions.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 4,
Li, Lei
Liu, Siyu
and
Ren, Weiyun
2023.
2-Local isometries on vector-valued differentiable functions.
Annals of Functional Analysis,
Vol. 14,
Issue. 4,
Jiménez-Vargas, A.
and
Miura, Takeshi
2023.
Approximate local isometries of derivative Hardy spaces.
Quaestiones Mathematicae,
Vol. 46,
Issue. 1,
p.
23.
Escolano, Gerardo M.
Peralta, Antonio M.
and
Villena, Armando R.
2024.
Lie–Trotter Formulae in Jordan–Banach Algebras with Applications to the Study of Spectral-Valued Multiplicative Functionals.
Results in Mathematics,
Vol. 79,
Issue. 1,
Wang, Liguang
Yang, Xueyan
and
Li, Lei
2024.
Variants of 2-local maps on function algebras.
Annals of Functional Analysis,
Vol. 15,
Issue. 3,