Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T08:38:50.143Z Has data issue: false hasContentIssue false
  • English
  • Français

Subordinate semigroups and order properties

Part of: Abstract harmonic analysis Linear function spaces and their duals

Published online by Cambridge University Press:  09 April 2009

Akitaka Kishimoto  and
Derek W. Robinson
Akitaka Kishimoto
Affiliation:
Department of Pure Mathematics, University of New South Wales, Kensington 2033, Australia
Derek W. Robinson
Affiliation:
Department of Pure Mathematics, University of New South Wales, Kensington 2033, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

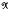Let St = exp{−tH}, Tt = exp{−tK}, be C0-semigroups on a Banach space . For appropriate f one can define subordinate semigroups Sft = exp{−tf(H)}, Ttf = exp{−tf(K)}, on 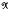and examine order properties of the pairs S, T, and Sf, Tf. If 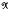, = Lp(X;dv) we define St≽ Tt ≽ 0 if St − Tt and Tt map non-negative functions into non-negative functions. Then for p fixed in the range 1 > p > ∞ we characterize the functions for which St ≽ Tt ≽ 0 implies Sft ≽ Tft ≽ 0 for each Lp(X;dv) and the converse is true for all Lp(X;dv). Further we give irreducibility criteria for the strict ordering of holomorphic semigroups. This extends earlier results for L2-spaces.

MSC classification

Secondary: 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.) 43A32: Other transforms and operators of Fourier type
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 31 , Issue 1 , June 1981 , pp. 59 - 76
Copyright
Copyright © Australian Mathematical Society 1981

References

Berg, C. and Forst, G. (1975), Potential theory on locally compact Abelian groups (Springer-Verlag).CrossRefGoogle Scholar
Beurling, A. and Deny, J. (1958), ‘Espaces de Dirichlet’, Acta Math. 99, 203–224.Google Scholar
Bochner, S. (1955), Harmonic analysis and the theory of probability, (Berkeley).CrossRefGoogle Scholar
Bratteli, O., Kishimoto, A. and Robinson, D. W. (1980), ‘Positivity and monotonicity properties of C0-semigroups I’, Comm. Math. Phys. 75, 67–84.CrossRefGoogle Scholar
Elliott, G. A., ‘Convergence of automorphisms in certain *-algebras’, J. Functional Analysis 11, 204–206.CrossRefGoogle Scholar
Hess, H., Schrader, R. and Uhlenbrock, D. W. (1977), ‘Domination of semigroups and generalization of Kato's inequality’, Duke Math. J. 44, 893–904.CrossRefGoogle Scholar
Hille, E. and Phillips, R. S. (1957), Functional analysis and semi-groups, (Amer. Math. Soc. Colloq. Publ. 31, Providence).Google Scholar
Karlin, S. (1959), ‘Positive operators’, J. Math. Mech. 8, 907–937.Google Scholar
Kishimoto, A. and Robinson, D. W. (1980), ‘Positivity and monotonicity properties of C0-semigroups’, Comm. Math. Phys. 75, 85–101.CrossRefGoogle Scholar
Krasnoselski, M. A. (1964), Positive solutions of operator equations, (Noordhoff).Google Scholar
Nelson, E. (1958), ‘A functional calculus using singular Laplace integrals’, Trans. Amer. Math. Soc. 88, 400–413.CrossRefGoogle Scholar
Philips, R. S. (1952), ‘On the generation of semigroups of linear operators’ Pacific J. Math. 2, 343–369.Google Scholar
Philips, R. S., ‘On linear transformation’, Trans. Amer. Math. Soc. 48, 516–541.CrossRefGoogle Scholar
Schoenberg, I. J. (1938), ‘Metric spaces and completely monotone functions’, Ann. Math. 39, 811–841.CrossRefGoogle Scholar
Simon, B. (1979), ‘Kato's inequality and the comparsion of semigroups’, J. Functional Analysis 32, 97–101.Google Scholar