Hostname: page-component-7b9c58cd5d-dkgms Total loading time: 0 Render date: 2025-03-13T19:16:12.503Z Has data issue: false hasContentIssue false
  • English
  • Français

The summability of formal solutions of functional equations

Published online by Cambridge University Press:  09 April 2009

J. D. Gray
J. D. Gray
Affiliation:
University of N.S.W., Kensington N.S.W.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1923 Nörlund [1] considered the difference equation

and showed that the formal solution of (1)

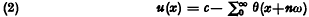
obtained by iteration, although in general divergent, is in fact Abel summable to a solution of (1). He writes the arbitary constant c as

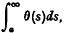
and thus the “principal solution” of the difference equation is

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 7 , Issue 2 , May 1967 , pp. 141 - 144
Copyright
Copyright © Australian Mathematical Society 1967

References

[1]Nörlund, N. E., ‘Mémoire sur le calcul aux différences finies’. Acta Math. 44 (1923), 71–211.CrossRefGoogle Scholar
[2]Bellman, R., ‘The summability of formal solutions of linear integral equations’. Duke Math. J. 17 (1950), 53–55.CrossRefGoogle Scholar
[3]Hille, E. & Phillips, R. S., Functional analysis and semi-groups (New York, 1958).Google Scholar
[4]Hardy, G. H., Divergent series (O.U.P. 1949).Google Scholar