Published online by Cambridge University Press: 09 April 2009
Let G denote a Hausdorff locally compact Abelian group which is nondiscrete and second countable. The main results (Theorems (2.2) and (2.3)) assert that, for any closed subset E of G there exists a pseudomeasure s on G whose singular support is E; and that if no portion of E is a Helson set, then such an s may be chosen having its support equal to E. There follow (Corollaries (2.2.4) and (2.3.2)) sufficient conditions for the relations 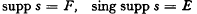 to hold for some pseudomeasure s, E and F being given closed subsets of G. These results are analogues and refinements of a theorem of Pollard [4] for the case G = R, which asserts the existence of a function in L∞(R) whose spectrum coincides with any preassigned closed subset of R.
to hold for some pseudomeasure s, E and F being given closed subsets of G. These results are analogues and refinements of a theorem of Pollard [4] for the case G = R, which asserts the existence of a function in L∞(R) whose spectrum coincides with any preassigned closed subset of R.