Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T05:36:53.886Z Has data issue: false hasContentIssue false
  • English
  • Français

SYMMETRY GEOMETRY BY PAIRINGS

Part of: Geometric closure systems

Published online by Cambridge University Press:  22 October 2018

G. CHIASELOTTI Open the ORCID record for G. CHIASELOTTI [Opens in a new window] ,
T. GENTILE  and
F. INFUSINO
G. CHIASELOTTI*
Affiliation:
Department of Mathematics and Computer Science, University of Calabria, Via Pietro Bucci, Cubo 30B, 87036 Arcavacata di Rende (CS), Italy email giampiero.chiaselotti@unical.it
T. GENTILE
Affiliation:
Department of Mathematics and Computer Science, University of Calabria, Via Pietro Bucci, Cubo 30B, 87036 Arcavacata di Rende (CS), Italy email gentile@mat.unical.it
F. INFUSINO
Affiliation:
Department of Mathematics and Computer Science, University of Calabria, Via Pietro Bucci, Cubo 30B, 87036 Arcavacata di Rende (CS), Italy email f.infusino@mat.unical.it
*
✉giampiero.chiaselotti@unical.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we introduce a symmetry geometry for all those mathematical structures which can be characterized by means of a generalization (which we call pairing) of a finite rectangular table. In more detail, let 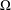$\unicode[STIX]{x1D6FA}$ be a given set. A pairing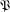$\mathfrak{P}$ on 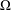$\unicode[STIX]{x1D6FA}$ is a triple 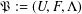$\mathfrak{P}:=(U,F,\unicode[STIX]{x1D6EC})$, where 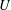$U$ and 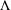$\unicode[STIX]{x1D6EC}$ are nonempty sets and 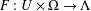$F:U\times \unicode[STIX]{x1D6FA}\rightarrow \unicode[STIX]{x1D6EC}$ is a map having domain 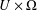$U\times \unicode[STIX]{x1D6FA}$ and codomain 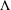$\unicode[STIX]{x1D6EC}$. Through this notion, we introduce a local symmetry relation on 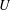$U$ and a global symmetry relation on the power set 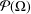${\mathcal{P}}(\unicode[STIX]{x1D6FA})$. Based on these two relations, we establish the basic properties of our symmetry geometry induced by 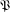$\mathfrak{P}$. The basic tool of our study is a closure operator 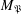$M_{\mathfrak{P}}$, by means of which (in the finite case) we can represent any closure operator. We relate the study of such a closure operator to several types of others set operators and set systems which refine the notion of an abstract simplicial complex.

Keywords

pairingsclosure systemssymmetryset partitions

MSC classification

Primary: 51D99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 106 , Issue 3 , June 2019 , pp. 342 - 360
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Alspach, B., ‘Isomorphism and Cayley graphs on abelian groups’, in: Graph Symmetry (eds. Hahn, G. and Sabidussi, G.) (Kluwer, Dordrecht, 1997), 1–22.Google Scholar
Alspach, B., Heinrich, K. and Varma, B. M., ‘Decompositions of complete symmetric digraphs into the oriented pentagons’, J. Aust. Math. Soc. A 28 (1979), 353–361.Google Scholar
Alspach, B., Marusic, D. and Nowitz, L., ‘Constructing graphs which are 1/2-transitive’, J. Aust. Math. Soc. A 56 (1994), 391–402.Google Scholar
Batten, L. M., ‘Rank functions of closure spaces of finite rank’, Discrete Math. 49(2) (1984), 113–116.Google Scholar
Batten, L. M. and Beutelspacher, A., The Theory of Finite Linear Spaces-Combinatorics of Points and Lines (Cambridge University Press, New York, 1993).Google Scholar
Batten, L. M. and Dover, J. M., ‘Blocking semiovals of type (1, m + 1, n + 1)’, SIAM J. Discrete Math. 14(4) (2001), 446–457.Google Scholar
Bayley, R. A., ‘Orthogonal partitions in designed experiments’, Des. Codes Cryptogr. 8(3) (1996), 45–77.Google Scholar
Bayley, R. A., Association Schemes: Designed Experiments, Algebra and Combinatorics (Cambridge University Press, Cambridge, 2004).Google Scholar
Berge, C., Hypergraphs: Combinatorics of Finite Sets (Elsevier, Amsterdam, 1984).Google Scholar
Birkhoff, G., Lattice Theory, 3rd edn (American Mathematical Society, Providence, RI, 1967).Google Scholar
Bisi, C. and Chiaselotti, G., ‘A class of lattices and boolean functions related to the Manickam–Miklös–Singhi conjecture’, Adv. Geom. 13(1) (2013), 1–27.Google Scholar
Bisi, C., Chiaselotti, G., Ciucci, D., Gentile, T. and Infusino, F., ‘Micro and macro models of granular computing induced by the indiscernibility relation’, Inf. Sci. 388–389 (2017), 247–273.Google Scholar
Bisi, C., Chiaselotti, G., Gentile, T. and Oliverio, P. A., ‘Dominance order on signed partitions’, Adv. Geom. 17(1) (2017), 5–29.Google Scholar
Bisi, C., Chiaselotti, G., Marino, G. and Oliverio, P. A., ‘A natural extension of the Young partition lattice’, Adv. Geom. 15(3) (2015), 263–280.Google Scholar
Bonacini, P., Gionfriddo, M. and Marino, L., ‘Nesting House-designs’, Discrete Math. 339(4) (2016), 1291–1299.Google Scholar
Cattaneo, G., Chiaselotti, G., Oliverio, P. A. and Stumbo, F., ‘A new discrete dynamical system of signed integer partitions’, European J. Combin. 55 (2016), 119–143.Google Scholar
Chiaselotti, G., Gentile, T. and Infusino, F., ‘Simplicial complexes and closure systems induced by indistinguishability relations’, C. R. Acad. Sci. Paris, Ser. I 355 (2017), 991–1021.Google Scholar
Chiaselotti, G., Gentile, T., Infusino, F. and Oliverio, P. A., ‘The adjacency matrix of a graph as a data table. A geometric perspective’, Ann. Mat. Pura Appl. (4) 196(3) (2017), 1073–1112.Google Scholar
Dohmen, K., ‘A broken-circuits-theorem for hypergraphs’, Arch. Math. 64 (1995), 159–162.Google Scholar
Eiter, T. and Gottlob, G., ‘Identifying the minimal transversals of a hypergraph and related problems’, SIAM J. Comput. 24 (1995), 1278–1304.Google Scholar
Kelarev, A., Ryan, J. and Yearwood, J., ‘Cayley graphs as classifiers for data mining: the influence of asymmetries’, Discrete Math. 309 (2009), 5360–5369.Google Scholar
Ksontini, R., ‘The fundamental group of the Quillen complex of the symmetric group’, J. Algebra 282 (2004), 33–57.Google Scholar
Kunzi, H.-P. A. and Yildiz, F., ‘Convexity structures in T 0 -quasi-metric spaces’, Topology Appl. 200 (2016), 2–18.Google Scholar
Lee, S. and Shih, M., ‘Sperner matroid’, Arch. Math. 81 (2003), 103–112.Google Scholar
Magner, A., Janson, S., Kollias, G. and Szpankowski, W., ‘On symmetry of uniform and preferential attachment graphs’, Electron. J. Combin. 21(3) (2014).Google Scholar
Martin, H. W., ‘Metrization of symmetric spaces and regular maps’, Proc. Amer. Math. Soc. 35 (1972), 269–274.Google Scholar
Rieder, J., ‘The lattices of matroid bases and exact matroid bases’, Arch. Math. 56 (1991), 616–623.Google Scholar
Sanahuja, S. M., ‘New rough approximations for n-cycles and n-paths’, Appl. Math. Comput. 276 (2016), 96–108.Google Scholar
Welsh, D. J. A., Matroid Theory (Academic Press, New York, 1976).Google Scholar
Xiang, S. W. and Yang, H., ‘Some properties of abstract convexity structures on topological spaces’, Nonlinear Anal. 67 (2007), 803–808.Google Scholar