Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T16:13:06.405Z Has data issue: false hasContentIssue false
  • English
  • Français

TANGENTIAL CONVERGENCE OF BOUNDED HARMONIC FUNCTIONS ON GENERALIZED SIEGEL DOMAINS

Published online by Cambridge University Press:  01 December 2008

M. SUNDARI
M. SUNDARI*
Affiliation:
Chennai Mathematical Institute, Plot H-1, SIPCOT IT Park, Padur P O, Siruseri, 603 103, India (email: sundari@cmi.ac.in)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that u is a bounded harmonic function on the upper half-plane such that 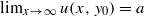for some y0>0. Then one can prove that 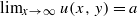for any other positive y. In this paper, we shall consider the algebra of radial integrable functions on H-type groups and obtain a similar result for bounded harmonic functions on generalized Siegel domains.

Keywords

Poisson kernelharmonic functiongeneralized Siegel domain
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 85 , Issue 3 , December 2008 , pp. 419 - 430
Copyright
Copyright © Australian Mathematical Society 2009

References

[1]Astengo, F. and Di Blasio, B., ‘A Paley–Wiener theorem on NA harmonic spaces’, Colloq. Math. 80 (1999), 211–233.Google Scholar
[2]Astengo, F. and Di Blasio, B., ‘The Schwartz space and homogeneous distributions on H-type groups’, Monatsh. Math. 132 (2001), 197–214.Google Scholar
[3]Cowling, M., Dooley, A., Korányi, A. and Ricci, F., ‘An approach to symmetric spaces of rank one via groups of Heisenberg type’, J. Geom. Anal. 8 (1998), 199–237.Google Scholar
[4]Cowling, M. and Haagerup, U., ‘Completely bounded multipliers of the Fourier algebra of a simple Lie group of real rank one’, Invent. Math. 96 (1989), 507–549.CrossRefGoogle Scholar
[5]Cygan, J., ‘A tangential convergence for bounded harmonic functions on a rank one symmetric space’, Trans. Amer. Math. Soc. 265 (1981), 405–418.CrossRefGoogle Scholar
[6]Damek, E., ‘Harmonic functions on semidirect extensions of type H nilpotent groups’, Trans. Amer. Math. Soc. 290 (1985), 375–384.Google Scholar
[7]Damek, E., ‘A Poisson kernel on Heisenberg type nilpotent groups’, Colloq. Math. 53 (1987), 239–247.Google Scholar
[8]Damek, E. and Ricci, F., ‘A class of nonsymmetric harmonic Riemannian spaces’, Bull. Amer. Math. Soc. 27 (1992), 139–142.Google Scholar
[9]Damek, E. and Ricci, F., ‘Harmonic analysis on solvable extensions of H-type groups’, J. Geom. Anal. 2 (1992), 213–248.Google Scholar
[10]Dixmier, J., ‘Opérateurs de rang fini dans les représentations unitaires’, Publ. Math. Inst. Hautes Études Sci. 6 (1960), 13–25.CrossRefGoogle Scholar
[11]Folland, G. B., A Course in Abstract Harmonic Analysis, Studies in Advanced Mathematics (CRC Press, Boca Raton, FL, 1995).Google Scholar
[12]Hulanicki, A. and Ricci, F., ‘A Tauberian theorem and tangential convergence for bounded harmonic functions on balls in ℂn’, Invent. Math. 62 (1980), 325–331.CrossRefGoogle Scholar
[13]Korányi, A., ‘Some applications of Gelfand pairs in classical analysis’, in: Harmonic Analysis and Group Representations (CIME, Napoli, 1982).Google Scholar
[14]Naimark, M. A., Normed Rings ( ed. L. F. Boron) (Wolters-Noordhoff, Groningen, 1970), Translated from first Russian edition.Google Scholar
[15]Thangavelu, S., Lectures on Hermite and Laguerre Expansions, Mathematical Notes, 42 (Princeton University Press, Princeton, NJ, 1993).Google Scholar
[16]Vemuri, M. K., ‘Realizations of the canonical representation’, Proc. Indian Acad. Sci. (Math. Sci.) 118 (2008), 115–131.CrossRefGoogle Scholar