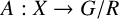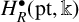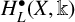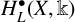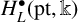TWISTED ACTIONS ON COHOMOLOGIES AND BIMODULES

Abstract

For closed subgroups L and R of a compact Lie group G, a left L-space X, and an L-equivariant continuous map $A:X\to G/R$, we introduce the twisted action of the equivariant cohomology $H_R^{\bullet }(\mathrm {pt},\Bbbk )$ on the equivariant cohomology $H_L^{\bullet }(X,\Bbbk )$. Considering this action as a right action, $H_L^{\bullet }(X,\Bbbk )$ becomes a bimodule together with the canonical left action of $H_L^{\bullet }(\mathrm {pt},\Bbbk )$. Using this bimodule structure, we prove an equivariant version of the Künneth isomorphism. We apply this result to the computation of the equivariant cohomologies of Bott–Samelson varieties and to a geometric construction of the bimodule morphisms between them.

1 Introduction

Let L be a topological group acting continuously on a topological space X. For any commutative ring $\Bbbk $ , the L-equivariant (sheaf) cohomology $H^{\bullet }_L(X,\Bbbk )$ is naturally a left $H^{\bullet }_L(\mathrm {pt},\Bbbk )$ -module, where $\mathrm {pt}$ is the singleton trivially acted upon by L. This module structure can explicitly be described as follows:

$$ \begin{align*} cm=a_X^{\star}(c)\cup m, \end{align*} $$

where $c\in H^{\bullet }_L(\mathrm {pt},\Bbbk )$ , $m\in H^{\bullet }_L(X,\Bbbk )$ , $a_X:X\to \mathrm {pt}$ is the constant map, $a_X^{\star }$ is the equivariant pull-back, and $\cup $ denotes the cup product.

The main idea of this paper is to define the structure of a right $H^{\bullet }_R(\mathrm {pt},\Bbbk )$ -module on $H^{\bullet }_L(X,\Bbbk )$ possibly for $R\ne L$ . Of course, if $L=R$ and we do not have any additional information about X, then we can do it, simply setting $ md=m \cup a_X^{\star }(d) $ . This construction is however very restrictive. Therefore, we define the right $H^{\bullet }_R(\mathrm {pt},\Bbbk )$ -module structure on $H^{\bullet }_L(X,\Bbbk )$ with the help of an L-equivariant map $A:X\to G/R$ , which we call the twisting map (Section 3.1). In this definition, refer to (3-2), the groups L and R are contained in a larger group G, which we assume to be a compact Lie group for the most part of the paper.

The main result of the paper is the proof of the following equivariant form of the Künneth isomorphism. Let X and Y be topological spaces, and $L,R,P,Q$ be closed subgroups of a compact Lie group G such that $R\subset P$ and $Q\subset P$ , the groups L and R act commutatively and continuously on X on the left and on the right, respectively, and Q acts continuously on Y on the left. Then we consider the space

$$ \begin{align*} X\mathop{\times}\limits_R P\mathop{\times}\limits_QY=X\times P\times Y/\sim, \end{align*} $$

where $\sim $ is the equivalence relation defined by $(x,p,y)\sim (xr,r^{-1}pq,q^{-1}y)$ for any $r\in R$ and $q\in Q$ . Let also $\alpha :X\to G$ be a continuous L- and R-equivariant map. It induces the morphism of left L-spaces $A:X/R\to G/R$ by $A(xR)=\alpha (x)R$ . Considering A as a twisting map, we get the structure of a right $H_R^{\bullet }(\mathrm {pt},\Bbbk )$ -module on $H_L^{\bullet }(X/R,\mathrm {pt})$ and thus the structure of a right $H_P^{\bullet }(\mathrm {pt},\Bbbk )$ -module through the natural morphism $H_P^{\bullet }(\mathrm {pt},\Bbbk )\to H_R^{\bullet }(\mathrm {pt},\Bbbk )$ . Similarly, the natural morphism $H_P^{\bullet }(\mathrm {pt},\Bbbk )\to H_Q^{\bullet }(\mathrm {pt},\Bbbk )$ defines the structure of a left $H_P^{\bullet }(\mathrm {pt},\Bbbk )$ -module on $H^{\bullet }_Q(Y,\Bbbk )$ by modifying the canonical left module structure. Then there exists a homomorphism of rings and bimodules

It is an isomorphism under certain restrictions (I)–(VIII) close to equivariant formality.

The theory we develop is illustrated by two basic examples: computation of the equivariant cohomology of the flag variety (Section 4.6) and the realization of the cohomology of the point with a twisted right action as a standard bimodule (Section 4.7).

Our main example however concerns Bott–Samelson varieties $\mathrm {BS}(\underline {t})$ in Section 5 for a sequence of reflections $\underline {t}$ . Here we use the original definition of these varieties by Bott and Samelson [BS]. Note that $\mathrm {BS}(\underline {t})$ is a left K-space for the maximal compact torus K. Thus, we can consider the K-equivariant cohomology $H_K^{\bullet }(\mathrm {BS}(\underline {t}),\Bbbk )$ for any commutative ring $\Bbbk $ . In Theorem 5.3, we establish the isomorphism of rings and ${\mathcal R}$ - ${\mathcal R}$ -bimodules

$$ \begin{align*} \theta_{\underline{t}}:{\mathcal R}\otimes_{{\mathcal R}^{t_1}}{\mathcal R}\otimes_{{\mathcal R}^{t_2}}\otimes\cdots\otimes_{{\mathcal R}^{t_n}}{\mathcal R}\stackrel\sim\to H_K^{\bullet}(\mathrm{BS}(\underline{t}),\Bbbk), \end{align*} $$

where $\underline {t}=(t_1,\ldots ,t_n)$ and ${\mathcal R}^{t_i}$ denotes the subring of $t_i$ -invariants of the K-equivariant cohomology of the point ${\mathcal R}$ . We call the tensor product in the left-hand side the Bott–Samelson bimodule. Compared with other constructions of similar isomorphisms (for example, [WW, Theorem 1.6]), our construction has the following advantages:

• • the reflections $t_i$ are not necessarily simple;

• • the proof is localization free;

• • $\theta _{\underline {t}}$ is constructed explicitly as a quotient of the composition of a pull-back and a (nonequivariant) Künneth isomorphism;

• • the ring of coefficients $\Bbbk $ can be any commutative ring of finite global dimension.

The isomorphisms $\theta _{\underline {t}}$ satisfy the quite expected concatenation property (Theorem 5.4) and their restrictions to the K-fixed points are computed (Theorem 5.7).

The explicit construction of the isomorphisms $\theta _{\underline {t}}$ pays off in Section 6, where we consider the morphisms of ${\mathcal R}$ - ${\mathcal R}$ -bimodules $H_K^{\bullet }(\mathrm {BS}(\underline {t}),\Bbbk )\to H_K^{\bullet }(\mathrm {BS}(\underline {r}),\Bbbk )$ . The morphisms we consider are built up from the elementary morphisms, which fall into two types: one-color morphisms and two-color morphisms. The former morphisms (Sections 6.2–6.3) exist for arbitrary reflections. However, we require the reflections to be simple for the latter morphisms (Sections 6.4–6.9), as the generalization to arbitrary reflections would require varieties more general than those considered in this paper.

Composing elementary morphisms horizontally as well as vertically, we get more general morphisms that are convenient to represent by planar diagrams [EW]. We assume here that such diagrams do not have horizontal tangent lines and that no two vertices have the same y-coordinate (Soergel graphs in the terminology of [EW]). We can cut any such diagram by horizontal lines into strips containing only one vertex. A typical picture looks like this:

We find a geometric description for any such horizontal strip as a pull-back or a push-forward or the composition of both. The first two cases are considered and computed in coordinates in Sections 6.2 and 6.3, and the compositions are considered in Section 6.5 and are extended horizontally in Section 6.9. One can see that the compositions are necessary only for strips containing two-color vertices. Such strips can be further cut to the upper and the lower parts, which are given by pull-backs and push-forwards, respectively. For example, the diagram above receives an additional cut. The corresponding strip turns into the following diagram:

This picture shows that we need to consider varieties more general than Bott–Samelson varieties (Section 6.4). We also prove that the normalization criterion for two-color morphisms holds (Lemma 6.4), which allows us to identify them with the morphism $f_{s,r}$ defined by Libedinsky in [Li, Lemme 4.7]. Note that Libedinsky proved in the same paper that in the case of simple reflections, all morphisms between Bott–Samelson modules are generated (as linear combinations) by morphisms corresponding to planar diagrams.

If we compose two-color diagrams differently as in Section 6.7, we obtain the Jones–Wenzl projectors, which we also represent by two-color vertices of the same valency as the vertices representing the morphisms $f_{s,r}$ . Some relations can be proved using the direct construction of the morphisms. The examples are given in Sections 6.3, 6.7, and 6.8. Note we prove these relations on the level of topology of the underlying varieties unlike [E, EKh], which argue on the level of polynomial algebras. We conjecture that all other relations defining the diagrammatic category [EW, (5.1)–(5.11)] as well as their versions for nonsimple reflections can also be proved similarly. In the case of sequences of simple reflections, these relations were proved in [RW] for morphisms between (shifted) Bott–Samelson parity complexes [RW, Ch. 10].

It also would be interesting to find a geometric description for morphisms represented by strips containing more than one vertex, at least in the case when all vertices of this strip are represented either by pull-backs or push-forwards.

2 Notation and basic constructions

2.1 Set theory

To avoid confusion with quotients, we denote the difference of sets by $-$ . For a sequence of indices $1\leqslant i_1<i_2<\cdots <i_k\leqslant n$ and sets $X_1,\ldots ,X_n$ , we denote by $\mathop{\rm pr}\nolimits _{i_1,i_2,\ldots ,i_k}$ the projection $X_1\times \cdots \times X_n\to X_{i_1}\times \cdots \times X_{i_k}$ to the corresponding coordinates.

Let X, Y, and S be sets, and $f:X\to S$ and $g:Y\to S$ be maps. The fiber product of X and Y with respect to f and g is the set

$$ \begin{align*} X\times_{f=g} Y=\{(x,y)\in X\times Y\mathbin{\rm |} f(x)=g(y)\}. \end{align*} $$

We often use the singleton $\mathrm {pt}$ whose unique element is denoted by ${pt}$ .

2.2 Sequences

We denote sequences by $\underline {s}$ , $\underline {t}$ , $\underline {r}$ , and so forth. The length n of a finite sequence $\underline {s}$ is denoted by $|\underline {s}|$ and its ith element is denoted by $s_i$ . Thus, $\underline {s}=(s_1,\ldots ,s_n)$ . The case $|\underline {s}|=0$ corresponds to the empty sequence $\underline {\varnothing }$ . If however $|\underline {s}|>0$ , then we get the truncated sequence $\underline {s}'=(s_1,\ldots ,s_{n-1})$ . If $\underline {t}=(t_1,\ldots ,t_m)$ is another sequence, we consider their concatenation $\underline {st}=(s_1,\ldots ,s_n,t_1,\ldots ,t_m)$ . Obviously, $|\underline {st}|=|\underline {s}|+|\underline {t}|$ . In Section 5.3, we use a similar notation for collection of integers $\underline {c}$ thought of as upper triangular matrices.

2.3 Modules

Let M and $M'$ be right modules over rings R and $R'$ , respectively. Suppose that there is an isomorphism of rings $\iota :R\stackrel \sim \to R'$ . Then a map $\mu :M\to M'$ is called an isomorphism of modules if it is an isomorphism of the underlying abelian groups and

(2-1) $$ \begin{align} \mu(mr)=\mu(m)\iota(r) \end{align} $$

for any $m\in M$ and $r\in R$ . We assume similar definitions for left modules and bimodules.

The tensor product of a right R-module M by a left R-module N is denoted as usual by $M\otimes _R N$ . If R is commutative, we can also consider the nth tensor power $N\otimes _R\cdots \otimes _RN$ with n factors, which we denote by $N^{\otimes _Rn}$ .

As the rings and (bi)modules in this paper are represented by cohomologies, they are naturally graded. The component of degree i of M is denoted by $M^i$ . In Section 6, we also consider the shift of grading: if M is a graded (bi)module and n is an integer, then we denote by $M(n)$ the graded (bi)module such that $M(n)^i=M^{n+i}$ .

2.4 Group actions and quotients

Let a group G act on a set X on the left. We denote this fact by $G\circlearrowright X$ . Then we denote by $G\mathop {\backslash } X$ the set of left G-orbits and by ${}^{G\!}X$ the set of G-fixed points of X, that is, of points $x\in X$ such that $gx=x$ for any $g\in G$ . We have the quotient map $X\to G\mathop {\backslash } X$ that sends x to $Gx$ . We use the notation $X/G$ and $X^G$ for right group actions. For example, let $P^1(\mathbb C)=({\mathbb C}^2-\{(0,0)\})/{\mathbb C}^\times $ , where ${\mathbb C}^\times $ acts as follows: $(z,w)c=(zc,wc)$ . This space is called the complex projective line. We denote the orbit in $P^1(\mathbb C)$ containing the pair $(z,w)$ by $[z,w]$ .

If groups L and R act on a set X on the left and on the right, respectively, then we say that the actions of L and R commute if $l(xr)=(lx)r$ for any $l\in L$ , $r\in R$ , and $x\in X$ . In this case, L acts on $X/R$ on the left and R acts on $L\mathop {\backslash } X$ on the right by $l(xR)=(lx)R$ and $(Lx)r=L(xr)$ , respectively.

Suppose that G acts on the left on both X and E. Then G acts on the left on the product $X\times E$ diagonally: $g(x,e)=(gx,ge)$ . We set

$$ \begin{align*} X\,{}_G\!\times\,E=G\mathop{\backslash}(X\times E). \end{align*} $$

We call the map $X\,{}_G\!\times \,E\to G\mathop {\backslash } E$ that maps any orbit $G(x,e)$ to $Ge$ the canonical projection. We denote canonical projections by $\mathop {\mathbf {can}}\nolimits $ . If $X'$ and $E'$ are other sets endowed with left G-actions, and $\alpha :X\to X'$ and $\beta :E\to E'$ are G-equivariant maps, then we denote by $\alpha {}\,{}_G\!\times \beta $ the map from $X\,{}_G\!\times \,E$ to $X'\,{}_G\!\times \,E'$ given by $G(x,e)\mapsto G(\alpha (x),\beta (e))$ .

2.5 Quotient products

Let $X_1,\ldots ,X_n$ be topological spaces and $G_1,\ldots ,G_{n-1}$ be topological groups such that each $G_i$ acts on the right on $X_i$ and on the left on $X_{i+1}$ . Suppose additionally that the actions of $G_{i-1}$ and $G_i$ on $X_i$ commute for each ${i=2,\ldots ,n-1}$ . Then we consider the following equivalence relation $\sim $ on ${X_1\times \cdots \times X_n}$ :

$$ \begin{align*} (x_1,\ldots,x_n)\sim(x_1g_1,g_1^{-1}x_2g_2,\ldots,g_{n-1}^{-1}x_n) \end{align*} $$

for any $g_1\in G_1$ , …, $g_{n-1}\in G_{n-1}$ . The quotient product is the following quotient space:

$$ \begin{align*} X_1\mathop{\times}\limits_{\;\,G_1}X_2\mathop{\times}\limits_{\;\,G_2}\cdots\!\!\!\!\!\mathop{\times}\limits_{\;\;\;\;\;\;G_{n-1}}X_n=X_1\times X_2\times\cdots\times X_n/\sim. \end{align*} $$

If $n=0$ , this space is just the singleton and if $n=1$ , this space is $X_1$ . The equivalence class containing $(x_1,x_2,\ldots ,x_n)$ is denoted by $[x_1:x_2:\cdots :x_n]$ . This product is clearly associative, that is,

$$\begin{align*}[x_1:\cdots :x_n]=[x_1:\cdots :x_{m-1}:[x_m:\cdots :x_k]:x_{k+1}:\cdots :x_n].\end{align*}$$

Moreover,

(2-2) $$ \begin{align}X_1\mathop{\times}\limits_{\;\,G_1}\cdots\!\!\!\!\!\mathop{\times}\limits_{\;\;\;\;\;\;G_{n-1}}X_n\cong X_1\mathop{\times}\limits_{\;\,G_1}\cdots\!\!\!\!\!\mathop{\times}\limits_{\;\;\;\;\;\;G_{i-1}}X_i\mathop{\times}\limits_{\;\,G_i}G_i\mathop{\times}\limits_{\;\,G_i}X_{i+1}\!\!\!\!\mathop{\times}\limits_{\;\;\;\;G_{i+1}}\cdots\!\!\!\!\!\mathop{\times}\limits_{\;\;\;\;\;\;G_{n-1}}X_n, \end{align} $$

where we assume that $[x_1:\cdots :x_n]=[x_1:\cdots :x_i:1:x_{i+1}:\cdots :x_n]$ .

If a group $G_0$ acts on the left on $X_1$ so that this action commutes with the right action of $G_1$ for $n>1$ , then $G_0$ also acts on the left on the above quotient product by $g_0[x_1:x_2:\cdots :x_n]=[g_0x_1:x_2:\cdots :x_n]$ . A similar fact is true if $G_n$ acts on $X_n$ on the right commuting with $G_{n-1}$ . In that case, we also consider the following quotient space:

$$ \begin{align*} X_1\mathop{\times}\limits_{\;\,G_1}X_2\mathop{\times}\limits_{\;\,G_2}\cdots\!\!\!\!\!\mathop{\times}\limits_{\;\;\;\;\;\;G_{n-1}}X_n/G_n=X_1\times X_2\times\cdots\times X_n/\approx, \end{align*} $$

where the equivalence relation $\kern1pt{\approx}\kern1pt $ is given by $(x_1,\ldots ,x_n\kern-0.1pt)\kern1.3pt{\approx}\kern1.3pt (x_1g_1,g_1^{-1}x_2g_2,\ldots ,g_{n-1}^{-1}x_ng_n\kern-0.1pt)$ for any $g_1\in G_1, \ldots,$ $g_{n-1}\in G_{n-1}$ , $g_n\in G_n$ . The equivalence class containing $(x_1,x_2,\ldots ,x_n)$ is denoted by . In view of the isomorphism

$$ \begin{align*} X_1\mathop{\times}\limits_{\;\,G_1}X_2\mathop{\times}\limits_{\;\,G_2}\cdots\!\!\!\!\!\mathop{\times}\limits_{\;\;\;\;\;\;G_{n-1}}X_n/G_n\cong X_1\mathop{\times}\limits_{\;\,G_1}X_2\mathop{\times}\limits_{\;\,G_2}\cdots\!\!\!\!\!\mathop{\times}\limits_{\;\;\;\;\;\;G_{n-1}}X_n\mathop{\times}\limits_{\;\;\;G_n}\mathrm{pt}, \end{align*} $$

we assume . It follows from (2-2) that

$$ \begin{align*} X_1\mathop{\times}\limits_{\;\,G_1}\cdots\!\!\!\!\!\mathop{\times}\limits_{\;\;\;\;\;\;G_{n-1}}X_n/G_n\cong X_1\mathop{\times}\limits_{\;\,G_1}\cdots\!\!\!\!\!\mathop{\times}\limits_{\;\;\;\;\;\;G_{i-1}}X_i\mathop{\times}\limits_{\;\,G_i}G_i\mathop{\times}\limits_{\;\,G_i}X_{i+1}\!\!\!\!\mathop{\times}\limits_{\;\;\;\;G_{i+1}}\cdots\!\!\!\!\!\mathop{\times}\limits_{\;\;\;\;\;\;G_{n-1}}X_n/G_n, \end{align*} $$

where we assume that . We make this identification, when appropriate.

2.6 Topology

We are going to use the following topological result.

Proposition 2.1. Let X and Y be topological spaces and $f:X\to Y$ be a continuous bijection. Suppose that there exists an open covering $Y=\bigcup _{i\in I}U_i$ and continuous functions $g_i:U_i\to X$ for each $i\in I$ such that $fg_i(y)=y$ for any $i\in I$ and $y\in U_i$ . Then f is a homeomorphism.

Proof. As the restrictions of $g_i$ and $g_j$ to $U_i\cap U_j$ coincide, we can glue these maps to the single continuous map g ([Du, Theorem III.9.4]). Then we get $fg=\mathrm {id}$ , whence $f^{-1}=g$ .

In this paper, we use the following terminology: a topological space X is called simply connected if it is path-connected, locally path-connected, and for any continuous function on the unit circle $f:S^1\to X$ , there exists a continuous function $g:D^1\to X$ on the closed unit disk such that $g|_{S^1}=f$ . Note that this definition deviates from the classical one in that we require local path-connectedness, which however is true for all cases we encounter (for example, topological manifolds).

Let E and B be G-spaces, and $p:E\to B$ be a continuous G-equivariant map. We say that p is a principal G-bundle if for each point $b\in B$ , there exist an open neighborhood $U\subset B$ and a G-equivariant homeomorphism $h:G\times U\stackrel \sim \to p^{-1}(U)$ for the left G-action or $h:U\times G\stackrel \sim \to p^{-1}(U)$ for the right G-action such that the respective diagram

is commutative. The G-equivariance of h means that for any $u\in U$ and $g_1,g_2\in G$ , there holds $h(g_1g_2,u)=g_1h(u,g_2)$ for the left G-action and $h(u,g_1g_2)=h(u,g_1)g_2$ for the right G-action.

Proposition 2.2 [Hu, Ch. 4, Proposition 5.3].

Let X and E be left G-spaces. Suppose that the quotient map $E\to G\mathop {\backslash } E$ is a principal G-bundle. Then the canonical projection $X\,{}_G\!\times \,E\to G\mathop {\backslash } E$ is a fiber bundle with fiber X.

Proposition 2.3. Let X and Y be right and left G-spaces, respectively. Let, moreover, H act continuously on Y on the right so that this action and the left action of G commute. Suppose that the quotient maps $X\to X/G$ and $Y\to Y/H$ are principal G- and H-bundles, respectively. Then the quotient map $f:X\mathop {\times }\limits _G Y\to X\mathop {\times }\limits _G Y/H$ is a principal H-bundle.

Proof. We use the notation of Section 2.5. Thus, . We also denote the quotient maps $X\to X/G$ and $Y\to Y/H$ by p and q, respectively.

Let be an arbitrary point of $X\mathop {\times }\limits _G Y/H$ . By the hypothesis of the lemma, there exist an open neighborhood U of $x_0G$ and a G-equivariant homeomorphism $\sigma $ such that the diagram

is commutative. Let $\mathbf g=\mathop{\rm pr}\nolimits _2\sigma ^{-1}$ . This is a continuous map from $p^{-1}(U)$ to G such that $\mathbf g(xg)=\mathbf g(x)g$ for any $x\in p^{-1}(U)$ and $g\in G$ .

There exists an open neighborhood V of $\mathbf g(x_0)y_0H$ and an H-equivariant homeomorphism $\tau $ such that the diagram

is commutative. Let $\mathbf h=\mathop{\rm pr}\nolimits _2\tau ^{-1}$ . This is a continuous map from $q^{-1}(V)$ to H such that $\mathbf h(yh)=\mathbf h(y)h$ for any $y\in q^{-1}(V)$ and $h\in H$ .

Let $\lambda :X\times Y/H\to X/G$ be the map given by and ${\mu :\lambda ^{-1}(U)\to Y/H}$ be the map given by . Obviously, both these maps are well defined and continuous. We set $W=\mu ^{-1}(V)$ . By our choice of U and V, we get . We define the function $\xi :W\times H\to X\mathop {\times }\limits _G Y$ by One can easily check that this map is well defined, continuous, and H-equivariant. Composing it with f,

This calculation proves that $\xi $ is actually a map to $f^{-1}(W)$ and that the following diagram is commutative:

It remains to prove that $\xi $ is a homeomorphism. This is true, as the inverse map is given by

2.7 Equivariant cohomology

Let G be a topological group. A principal G-bundle $E\to B$ is called universal if the total space E is contractible. We define the G-equivariant cohomology of a left G-space X with coefficients in a commutative ring $\Bbbk $ by

$$ \begin{align*} H^{\bullet}_G(X,\Bbbk)=H^{\bullet}(X\,{}_G\!\times\,E,\Bbbk). \end{align*} $$

Considering the canonical projection $\mathop {\mathbf {can}}\nolimits :X\,{}_G\!\times \,E\to G\mathop {\backslash } E\cong \mathrm {pt}\,{}_G\!\times \,E$ , we obtain the map $\mathop {\mathbf {can}}\nolimits ^*:H^{\bullet }_G(\mathrm {pt},\Bbbk )\to H^{\bullet }_G(X,\Bbbk )$ . This map makes $H^{\bullet }_G(X,\Bbbk )$ into a left $H^{\bullet }_G(\mathrm {pt},\Bbbk )$ -module by

$$ \begin{align*} am=\mathop{\mathbf{can}}\nolimits^*(a)\cup m, \end{align*} $$

where $a\in H^{\bullet }_G(\mathrm {pt},\Bbbk )$ and $m\in H^{\bullet }_G(X,\Bbbk )$ . This module does not depend on the choice of the universal bundle $E\to B$ . This fact is discussed in Corollary 3.2. We call this left action of $H^{\bullet }_G(\mathrm {pt},\Bbbk )$ canonical.

The similar right action of $H^{\bullet }_G(\mathrm {pt},\Bbbk )$ on $H^{\bullet }_G(X,\Bbbk )$ given by $ma=m\cup \mathop {\mathbf {can}}\nolimits ^*(a)$ is also called canonical. We use it in Section 4.6.

If $X'$ is another left G-space and $f:X\to X'$ is a continuous G-equivariant map, then we have the continuous map $f\,{}_G\!\times \,\mathrm {id}:X\,{}_G\!\times \,E\to X'\,{}_G\!\times \,E$ . This map induces the pull-back

$$ \begin{align*} (f\,{}_G\!\times\,\mathrm{id})^*:H^{\bullet}_G(X',\Bbbk)\to H^{\bullet}_G(X,\Bbbk) \end{align*} $$

between cohomologies. We use the notation $f^{\star }=(f\,{}_G\!\times \,\mathrm {id})^*$ to distinguish between the ordinary and the equivariant pull-backs. For example, $a_X^{\star }=\mathop {\mathbf {can}}\nolimits ^*$ , where ${a_X:X\to \mathrm {pt}}$ is the constant map.

2.8 Stiefel manifolds

Let G be a compact Lie group. As G can be considered a closed subgroup of the unitary group $U({\mathfrak n}_{G})$ for ${\mathfrak n}_{G}$ big enough which will be thought of as a function of $G$ throughout the paper, we explain how to find a universal principal $U({\mathfrak n}_{G})$ -bundle. For any natural number $N>{\mathfrak n}_{G}$ , we consider the Stiefel manifold (this space is usually denoted by $W_{N,{\mathfrak n}_{G}}$ or $V_{{\mathfrak n}_{G}}({\mathbb C}^N)$ or ${\mathbb C} V_{N,{{\mathfrak n}_{G}}}$ . We also transpose matrices, as we want to have a left action of $U({\mathfrak n}_{G})$ )

$$ \begin{align*} E^N=\{A\in \mathop{\rm Mat}\nolimits_{{{\mathfrak n}_{G}},N}(\mathbb C)\mathbin{\rm |} A\bar A^T=I_{{\mathfrak n}_{G}}\}, \end{align*} $$

where $\mathop{\rm Mat}\nolimits _{{{\mathfrak n}_{G}},N}({\mathbb C})$ is the space of ${\mathfrak n}_{G}\times N$ complex matrices with respect to the metric topology and $I_{{\mathfrak n}_{G}}$ is the identity ${\mathfrak n}_{G}\times {\mathfrak n}_{G}$ matrix. The group $U({\mathfrak n}_{G})$ acts on $E^N$ on the left by multiplication. Similarly, $U(N)$ acts on $E^N$ on the right by multiplication. The last action is transitive and commutes with the left action of $U({\mathfrak n}_{G})$ . The quotient space $\mathop{\rm Gr}\nolimits ^N=U({\mathfrak n}_{G})\mathop {\backslash } E^N$ is called the Grassmanian and the corresponding quotient map ${E^N\to \mathop{\rm Gr}\nolimits ^N}$ is a principal $U({\mathfrak n}_{G})$ -bundle. Note that the group $U(N)$ also acts on $\mathop{\rm Gr}\nolimits ^N$ by the right multiplication. For $N<N'$ , we have the smooth embedding $E^N\hookrightarrow E^{N'}$ by adding $N'-N$ zero columns to the right.

Taking the direct limits

$$ \begin{align*} E=\mathop{\rm lim}\limits_{\longrightarrow} E^N,\quad \mathop{\rm Gr}\nolimits=\mathop{\rm lim}\limits_{\longrightarrow}\mathop{\rm Gr}\nolimits^N, \end{align*} $$

we get a universal principal $U({\mathfrak n}_{G})$ -bundle $E\to \mathop{\rm Gr}\nolimits $ . These spaces satisfy the following properties [Bo, Proposition 9.1].

Proposition 2.4

1. (1) $E^N$ is simply connected.

2. (2) $H^n(E^N,\Bbbk )=0$ for $0<n\leqslant 2(N-{\mathfrak n}_{G})$ .

3. (3) $H^n(E^N,\Bbbk )$ is free of finite rank for any n.

Corollary 2.5. For any closed connected subgroup L of G, the space $L\mathop {\backslash } E^N$ is simply connected.

Proof. As $E^N\to L\mathop {\backslash } E^N$ is a fiber bundle with fiber L, the result follows from Propositions 2.4, (1), and the long exact sequence of homotopy groups

$$ \begin{align*} \{1\}=\pi_1(E^N)\to \pi_1(L\mathop{\backslash} E^N)\to \pi_0(L)=\{1\}. \\[-35pt]\end{align*} $$

Proposition 2.6. Let L be a closed subgroup of G and X be a left L-space. Then the restriction map

$$ \begin{align*} H_L^n(X,\Bbbk)\to H^n(X\,{}_L\!\times E^N,\Bbbk) \end{align*} $$

is an isomorphism for $n\leqslant 2(N-{\mathfrak n}_{G})$ .

Proof. Let us consider the triple product $X\times E^N\times E$ with respect to the diagonal action of L, the natural embedding $\iota :X\,{}_L\!\times E^N\hookrightarrow X\,{}_L\!\times E$ , and the map $\Delta :X\times E^N\to X\times E^N\times E$ given by $(x,e)\mapsto (x,e,e)$ . Then we have the following commutative diagram:

Here, the isomorphisms follow from Propositions 2.4, (2), and the Vietoris–Begle theorem in the form [S2, Corollary 14], as the quotient maps

$$ \begin{align*} L\mathop {\backslash }\mathop{\rm pr}\nolimits _{1,2}:L\mathop {\backslash }(X\times E^N\times E)\to X\,{}_L\!\times E^N,\quad L\mathop {\backslash }\mathop{\rm pr}\nolimits _{1,3}:L\mathop {\backslash }(X\times E^N\times E)\to X\,{}_L\!\times E \end{align*} $$

are fiber bundles with fibers E and $E^N$ , respectively. From the left triangle, it follows that $(L\mathop {\backslash } \Delta )^*$ is an isomorphism. Therefore, it follows from the right triangle that $\iota ^*$ is also an isomorphism.

Corollary 2.7. Let L be a closed subgroup of G, X be a left L-space, and ${{\mathfrak n}_{G}<N' <N}$ . Then the restriction map

$$ \begin{align*} H^n(X\,{}_L\!\times E^N,\Bbbk)\to H^n(X\,{}_L\!\times E^{N'},\Bbbk) \end{align*} $$

is an isomorphism for $n\leqslant 2(N-{\mathfrak n}_{G})$ .

Remark 2.8. We always mean the choice of $E$ as the direct limit of $E^N$ in the remainder of the paper. If, however, we replace it by $E^N$ , then we write $f^N$ instead of f, where f is either a map between spaces whose definitions depend on E or a subset of such a space. We refer to $f^N$ as a compact version of f.

2.9 Ordinary push-forward

For any topological space X, we consider the dualizing complex $\omega _X=a_X^!\Bbbk $ [KS, Definition 3.1.16]. This complex allows us to define the Borel–Moore homology $H^{\mathrm {BM}}_i(X,\Bbbk )={\mathbb H}^{-i}(X,\omega _X)$ , where ${\mathbb H}^{\bullet }(X,\_\!\_\,)$ is the hypercohomology functor [Di, Definition 2.1.4].

Any proper map $f:X\to Y$ induces the push-forward map $f_*:H^{\mathrm {BM}}_i(X,\Bbbk )\to H^{\mathrm {BM}}_i(Y,\Bbbk )$ . Suppose additionally that X and Y are orientable topological manifolds of dimensions n and m, respectively. This means that there exist isomorphisms $\omega _X\cong \Bbbk [n]$ and $\omega _Y\cong \Bbbk [m]$ , which we fix. Then we get the following map between the cohomologies:

which we also denote by $f_*$ . This map is also called the Gysin map. It has the following property [I, IX.7.3].

Proposition 2.9 (Projection formula).

For any proper continuous map $f:X\to Y$ between oriented topological manifolds, $\xi \in H^{\bullet }(X,\Bbbk )$ and $\eta \in H^{\bullet }(Y,\Bbbk )$ , there holds

$$ \begin{align*} f_*(\xi\cup f^*\eta)=f_*(\xi)\cup\eta. \end{align*} $$

2.10 Orientation of quotient spaces

Let U be an oriented subspace of an oriented real vector space V. We fix the following orientation of the quotient space $V/U$ . Let $v_1,\ldots ,v_n$ be an oriented basis of V such that $v_1,\ldots ,v_m$ is an oriented basis of U for some $m\leqslant n$ . Then the orientation of $V/U$ is defined by declaring the basis ${v_{m+1}+U,\ldots ,v_n+U}$ to be oriented. We define the orientation of the quotient of oriented vector bundles by defining the orientation of each fiber using the rule just described.

2.11 Compatibly oriented squares

We follow here the presentation of this topic by Fulton [F, Appendix A: Algebraic topology, Section 5]. For an embedding $X\hookrightarrow Y$ of smooth manifolds, we denote by $\nu _{X,Y}$ the normal bundle of X in Y. If X and Y are oriented, then $\nu _{X,Y}$ is orientated as described in Section 2.10.

Consider a Cartesian square

where $X,X',Y,Y'$ are compact smooth oriented manifolds and $f,f',g,g'$ are smooth maps. By the Whitney embedding theorem (for example, [Lee, Theorem 6.15]), there exists a closed embedding $\iota :X\hookrightarrow {\mathbb R}^M$ , where $M=2\dim X+1$ . Then we get the closed embedding $f\times \iota :X\hookrightarrow Y\times {\mathbb R}^M$ and also the closed embedding $f'\times \iota g':X'\hookrightarrow Y'\times {\mathbb R}^M$ .

We say that the above square is compatibly oriented if

(2-3) $$ \begin{align} \nu_{X',Y'\times{\mathbb R}^M}\cong (g')^*\nu_{X,Y\times{\mathbb R}^M} \end{align} $$

as oriented vector bundles. If this isomorphism holds and $\dim X-\dim Y=\dim X'-\dim Y'$ , then

(2-4) $$ \begin{align} f^{\prime}_*(g')^*=g^*f_*. \end{align} $$

We refer to this property as the naturality of the push-forward.

2.12 Smooth structures on Borel constructions

Let L be a closed connected subgroup of a compact Lie group G. By the quotient manifold theorem [Lee, Theorem 21.10], the space $L\mathop {\backslash } E^N$ is a smooth manifold. It is orientable being simply connected by Corollary 2.5. Therefore, we consider only local coordinates on $L\mathop {\backslash } E^N$ from a chosen oriented atlas.

Let X be any smooth manifold acted upon smoothly by L on the left. Applying the quotient manifold theorem once again, we get that the space $X\;{}_L\! \times E^N$ is a smooth manifold. Its smooth structure can be described as follows. Let $L(x_0,e_0)$ be an arbitrary point of $X\;{}_L\! \times E^N$ . There exists a coordinate chart U of $L\mathop {\backslash } E^N$ containing $Le_0$ . Let $(u^1,\ldots ,u^k)$ be the coordinates on U.

Shrinking U if necessary, we may suppose that the restriction of the fiber bundle $p:E^N\to L\mathop {\backslash } E^N$ to U is a trivial bundle, that is, there exists an L-equivariant diffeomorphism h such that the diagram

is commutative. We set ${\mathbf l}=\mathop{\rm pr}\nolimits _1h^{-1}$ . This map is smooth and has the usual (refer to the proof of Proposition 2.3) property ${\mathbf l}(le)=l{\mathbf l}(e)$ for any $l\in L$ and $e\in p^{-1}(U)$ .

The restriction of the fiber bundle $\mathop {\mathbf {can}}\nolimits :X\;{}_L\! \times E^N\to L\mathop {\backslash } E^N$ to U is also trivial. This trivialization is given by $L(x,e)\mapsto ({\mathbf l}(e)^{-1}x,Le)$ . Then the coordinates in the vicinity of $L(x_0,e_0)$ are given by the local coordinates $(x^1,\ldots ,x^n,u^1,\ldots ,u^k)$ , where $(x^1,\ldots ,x^n)$ are the local coordinates on X in the vicinity of ${\mathbf l}(e_0)^{-1}x_0$ . If $(\tilde x^1,\ldots ,\tilde x^n,\tilde u^1,\ldots ,\tilde u^k)$ are different local coordinates in a vicinity of $L(x_0,e_0)$ with a possibly different trivialization function $\tilde {\mathbf l}$ , then the Jacobian matrix of the base change is equal to

$$ \begin{align*} \frac{\partial(\tilde x^1,\ldots,\tilde x^n,\tilde u^1,\ldots,\tilde u^k)}{\partial(x^1,\ldots,x^n,u^1,\ldots,u^k)}(L(x,e)) = \left( \begin{array}{@{}cc@{}} \dfrac{\partial(\tilde f^1,\ldots,\tilde f^n)}{\partial(x^1,\ldots,x^n)}({\mathbf l}(e)^{-1}x)&0\\[8pt] *& \dfrac{\partial(\tilde u^1,\ldots,\tilde u^k)}{\partial(u^1,\ldots,u^k)}(Le) \end{array} \right), \end{align*} $$

where f is the map $f(x)=\tilde {\mathbf l}(e)^{-1}{\mathbf l}(e)x$ and $\tilde f^i=\tilde x^if$ . Note that the multiplication constant $\tilde {\mathbf l}(e)^{-1}{\mathbf l}(e)$ smoothly depends only on $Le$ . The multiplication by this constant is responsible to the $*$ -part in the above matrix. This part is the zero matrix if we do not change the local trivialization of $E^N\to L\mathop {\backslash } E^N$ .

If X is oriented, then L acts on X by orientation-preserving diffeomorphisms. Hence,

$$ \begin{align*} \det\frac{\partial(\tilde f^1,\ldots,\tilde f^n)}{\partial(x^1,\ldots,x^n)}({\mathbf l}(e)^{-1}x)>0 \end{align*} $$

and the atlas described above on $X\;{}_L\! \times E^N$ is oriented.

2.13 Equivariant push-forward

Let X and Y be compact smooth oriented manifolds acted upon smoothly on the left by a closed connected subgroup L of a compact Lie group G. Let $f:Y\to X$ be a smooth L-equivariant map. For any $N>{\mathfrak n}_{G}$ , we get the smooth proper map $f\;{}_L\! \times \mathrm {id}:Y\;{}_L\! \times E^N\to X\;{}_L\! \times E^N$ , which we denote by $f^N$ . As both the domain and codomain of this map are smooth oriented manifolds, we can consider the ordinary push-forward

$$ \begin{align*} f^N_*:H^n(Y\;{}_L\! \times E^N,\Bbbk)\to H^{n+d}(X\;{}_L\! \times E^N,\Bbbk), \end{align*} $$

where $d=\dim X-\dim Y$ . So by Proposition 2.6, we actually get the map

$$ \begin{align*} f_\star:H^n_L(Y,\Bbbk)\to H_L^{n+d}(X,\Bbbk), \end{align*} $$

as soon as $n\leqslant \min \{2(N-{\mathfrak n}_{G}),2(N-{\mathfrak n}_{G})-d\}$ , defined by

(2-5) $$ \begin{align} f_\star(m)=(i_X^*)^{-1}f_*^Ni_Y^*(m) \end{align} $$

for $m\in H^n_L(Y,\Bbbk )$ , where $i_X:X\;{}_L\! \times E^N\hookrightarrow X\;{}_L\! \times E$ and $i_Y:Y\;{}_L\! \times E^N\hookrightarrow Y\;{}_L\! \times E$ are the natural embeddings.

We claim that the definition of $f_\star $ does not depend of N. Indeed, let $N'>N$ . In this case, we have the map $f^{\prime }_\star $ defined by a formula similar to (2-5). To prove that $f^{\prime }_\star =f_\star $ , we consider the diagram

As both triangles and trapezoids are commutative, it suffices to prove that the perimeter is also so. This fact follows from (2-4) as soon as we prove that the square

is compatibly oriented.

First note that the embedding $E^N\hookrightarrow E^{N'}$ produces an embedding $L\mathop {\backslash } E^N\hookrightarrow L\mathop {\backslash } E^{N'}$ . Therefore, we always choose the coordinates $(u^1,\ldots ,u^{k'})$ on an open subspace ${U'\subset L\mathop {\backslash } E^{N'}}$ so that the intersection $U'\cap E^N$ is defined by the equalities ${u^{k+1}=0,\ldots ,u^{k'}=0}$ . Shrinking $U'$ if necessary, we assume that the fiber bundle $p':E^{N'}\to L\mathop {\backslash } E^{N'}$ is trivial and consider the trivialization function ${\mathbf l}':(p')^{-1}(U')\to L$ as in Section 2.12.

Let $\iota :Y\;{}_L\! \times E^{N'}\hookrightarrow {\mathbb R}^M$ be an embedding. We denote by $x^1,\ldots ,x^n$ , $y^1,\ldots ,y^m$ , and $z^1,\ldots ,z^M$ local coordinates on X, Y, and ${\mathbb R}^M$ , respectively.

We abbreviate

$$ \begin{align*} \mathbb B'=(X\;{}_L\! \times E^{N'})\times{\mathbb R}^M,\quad \mathbb B=(X\;{}_L\! \times E^N)\times{\mathbb R}^M. \end{align*} $$

According to the general plan described in Section 2.11, we need to consider the embedding $ \beta '=f^{N'}\times \iota :Y\;{}_L\! \times E^{N'}\hookrightarrow \mathbb B' $ , and its pullback $ \beta :Y\;{}_L\! \times E^N\hookrightarrow \mathbb B $ being in our case simply the restriction of $\beta '$ , that is, $\beta =f^N\times \iota |_{Y{}_L\! \times E^N}$ .

Let $a\in Y{}_L\! \times E^N$ be an arbitrary point. We set $b=\beta (a)=\beta '(a)$ . Choosing the representation $a=L(y,e)$ with $\mathbf l'(e)=1$ , we compute the differential

$$ \begin{align*}T_a\beta ':T_a(Y{}_L\! \times E^{N'})\hookrightarrow T_b\mathbb B'\end{align*} $$

in coordinates as follows:

(2-6) $$ \begin{align} T_a\beta'\bigg(\frac{\partial}{\partial y^i}\bigg)=\sum_{j=1}^n\frac{\partial f^j}{\partial y^i}(y)\frac{\partial}{\partial x^j}+\sum_{q=1}^M\frac{\partial\iota^q}{\partial y^i}(a)\frac{\partial}{\partial z^q},\quad T_a\beta'\bigg(\frac{\partial}{\partial u^i}\bigg)=\frac{\partial}{\partial u^i}+\sum_{q=1}^M\frac{\partial\iota^q}{\partial u^i}(a)\frac{\partial}{\partial z^q}. \end{align} $$

Therefore, we can choose $v_1,\ldots ,v_r\in T_b\mathbb B'$ in the span of ${\partial }/{\partial x^j}$ and ${\partial }/{\partial z^q}$ so that the sequence

(2-7) $$ \begin{align} \bigg(T_a\beta'\bigg(\frac{\partial}{\partial y^1}\bigg),\ldots,T_a\beta'\bigg(\frac{\partial}{\partial y^m}\bigg),T_a\beta'\bigg(\frac{\partial}{\partial u^1}\bigg),\ldots,T_a\beta'\bigg(\frac{\partial}{\partial u^{k'}}\bigg),v_1,\ldots,v_r\bigg) \end{align} $$

is an oriented basis of $T_b\mathbb B'$ . Note that our choice guarantees that $v_1,\ldots ,v_r\in T_a\mathbb B$ . By the convention of Section 2.10, the sequence $(v_1+\mathop{\rm im} T_a\beta ',\ldots ,v_r+\mathop{\rm im} T_a\beta ')$ is an oriented basis of the fiber $(\nu _{Y{}_L\! \times E^{N'},\mathbb B'})_b=T_b\mathbb B'/\mathop{\rm im} T_a\beta '$ . By (2-6), the transition matrix from (2-7) to the oriented basis

$$ \begin{align*} \bigg(\frac{\partial}{\partial x^1},\ldots,\frac{\partial}{\partial x^n},\frac{\partial}{\partial u^1},\ldots,\frac{\partial}{\partial u^{k'}},\frac{\partial}{\partial z^1},\ldots,\frac{\partial}{\partial z^M}\bigg) \end{align*} $$

of $T_b\mathbb B'$ has the form

$$ \begin{align*} \left( \begin{array}{ccc} F&0&V\\ 0&I_{k'}&0\\ Z_1&Z_2&Z_3 \end{array} \right) \end{align*} $$

for the matrices F, V, $Z_1$ , $Z_2$ , $Z_3$ of sizes $n\times m$ , $n\times r$ , $M\times n$ , $M\times k'$ , $M\times r$ , respectively. By construction, the determinant of the above matrix is positive. Note that $k'-k=2(N'-N){\mathfrak n}_{G}$ is even. Therefore, if we cross out the rows and columns corresponding to coordinates $u^{k+1},\ldots ,u^{k'}$ , we get a matrix with positive determinant. Repeating the above arguments for the space $\mathbb B$ (in reverse order), we get that $(v_1+\mathop{\rm im} T_a\beta ,\ldots ,v_r+\mathop{\rm im} T_a\beta )$ is an oriented basis of the fiber $(\nu _{Y{}_L\! \times E^N,\mathbb B})_b$ . This fact proves (2-3).

2.14 Semisimple groups

Let G be a semisimple compact Lie group. Then G can be described externally as the set of points fixed by some analytic automorphism of the corresponding complex Chevalley group $G^c$ [St, Remark following Theorem 16].

We consider a maximal torus $K<G$ and the Weyl group $W=N_G(K)/K$ . For any $w\in W$ , we arbitrarily choose its lifting $\dot w\in N_G(K)$ . We use the abbreviation $wK=\dot {w}K$ .

The group G has the Bruhat decomposition $G=\bigsqcup _{w\in W}K_w$ , where $K_w=G\cap (BwB)$ and B is the Borel subgroup of $G^c$ corresponding to a chosen Bruhat order $\leqslant $ on W [St, Corollary 5 of Lemma 45]. Taking the quotient, we get the decomposition ${G/K=\bigsqcup _{w\in W}K_w/K}$ into Schubert cells. We can compute their closures, called Schubert varieties, as $\overline {K_w/K}=\bigsqcup _{w'\leqslant w}K_{w'}$ .

We have $K\cong (S^1)^d$ for some d, where $S^1$ is the unit circle. We get the map ${\rho _w:E\to E}$ given by $\rho _w(e)=\dot we$ . This map factors through the action of K as ${\rho _w(ke)=k'\rho _w(e)}$ , where $k'=\dot wk\dot w^{-1}\in K$ , and we get the map $K\mathop {\backslash }\rho _w:K\mathop {\backslash } E\to K\mathop {\backslash } E$ and hence its pull-back $(K\mathop {\backslash }\rho _w)^*:H^{\bullet }_K(\mathrm {pt},\Bbbk )\to H^{\bullet }_K(\mathrm {pt},\Bbbk )$ . We think of this map as a left action of W on $H^{\bullet }_K(\mathrm {pt},\Bbbk )$ :

(2-8) $$ \begin{align} w(\mu)=(K\mathop{\backslash}\rho_{w^{-1}})^*(\mu). \end{align} $$

This formula agrees with the following standard representation of $H^{\bullet }_K(\mathrm {pt},\Bbbk )$ as a polynomial ring, refer to [Br, Section 1, Example 2] and [J, 1.7, 1.8]. Let us consider for each character $\lambda :K\to S^1$ the representation ${\mathbb C}_\lambda $ being the field of complex numbers ${\mathbb C}$ as the vector space and having the following left K-action: $kc=\lambda (k)c$ . We denote the line bundle $\mathop {\mathbf {can}}\nolimits :({\mathbb C}_\lambda ){}_K\! \times E\to K\mathop {\backslash } E$ by $\mathcal L(\lambda )$ . Its Euler class (that is, the first Chern class) $\mathop{\rm Eu}\nolimits (\mathcal L(\lambda ))$ is identified with $\lambda $ itself. Thus, choosing $\varepsilon _1,\ldots ,\varepsilon _d$ freely generating the character group of K, we get that the cohomology ring $H_K^{\bullet }(\mathrm {pt},\Bbbk )$ is a polynomial ring over $\Bbbk $ in variables $\varepsilon _i$ .

For any root $\alpha $ , we denote by $G_\alpha $ the subgroup of G generated by the image of the root homomorphism $\varphi _\alpha :\mathop {\rm SU}\nolimits _2\to G$ and the torus K [BS, Ch. III (3.1)]. An alternative (external) description of this subgroup is given in [St, Lemma 45]. As $G_\alpha =G_{-\alpha }$ , we can denote $G_{\omega _\alpha }=G_\alpha $ , where $\omega _\alpha \in W$ is the reflection through the plane perpendicular to $\alpha $ . We call elements $\omega _\alpha $ reflections. In what follows, for any reflection t, we denote by $\alpha _t$ the positive root such that $t=\omega _{\alpha _t}$ . We also reserve the letter s (with indices or accents, primed or underlined) to denote simple reflections or sequences of simple reflections. This notation is used only in Sections 6.4–6.9.

3 The tensor product morphism

3.1 Twisted action

Let G be a topological group, and L and R be subgroups. We assume that L and R act on G on the left and on the right, respectively, by multiplication. As both actions commute, the group L acts continuously on the quotient space $G/R$ on the left.

Let X be another left L-space and $A:X\to G/R$ be an L-equivariant continuous map. We call A a twisting map. For any left G-space E, the map A allows us to define the map

$$ \begin{align*} v_A:X\,{}_L\!\times\,E\to R\mathop{\backslash} E \end{align*} $$

by

(3-1) $$ \begin{align} L(x,e)\mapsto A(x)^{-1}e. \end{align} $$

Note that $A(x)^{-1}\in R\mathop {\backslash } G$ . The reader can easily check that $v_A$ is well defined and continuous. We call this map the projection twisted by A.

Let us suppose that the quotient maps $E\to L\mathop {\backslash } E$ and $E\to R\mathop {\backslash } E$ are universal principal L- and R-bundles, respectively. Then we get the map between cohomologies $v_A^*:H^{\bullet }_R(\mathrm {pt},\Bbbk )\to H^{\bullet }_L(X,\Bbbk )$ , which induces the following right $H^{\bullet }_R(\mathrm {pt},\Bbbk )$ -action on $H^{\bullet }_L(X,\Bbbk )$ :

(3-2) $$ \begin{align} mb=m\cup v_A^*(b). \end{align} $$

We call this action the action twisted by A.

A priori, this construction of a right module depends on the choice of E. However, we get the following result.

Lemma 3.1. Up to isomorphism, the right $H^{\bullet }_R(\mathrm {pt},\Bbbk )$ -module $H^{\bullet }_L(X,\Bbbk )$ is independent of the choice of E.

Proof. Let $\widetilde E$ be another left G-space such that $\widetilde E\to L\mathop {\backslash }\widetilde E$ and $\tilde E\to R\mathop {\backslash }\tilde E$ are universal principal L- and R-bundles, respectively. We use the following notation only in this proof:

$$ \begin{align*} \widetilde H_L^{\bullet}(X,\Bbbk)=H^{\bullet}(X{}_L\!\times\widetilde E,\Bbbk), \quad \widetilde H_R^{\bullet}(\mathrm{pt},\Bbbk)=H^{\bullet}(R\mathop{\backslash}\widetilde E,\Bbbk). \end{align*} $$

We also have the map $\tilde v_A:X{}_L\!\times \widetilde E\to R\mathop {\backslash }\widetilde E$ similar to $v_A$ also given by (3-1). This map defines the structure of a right $\widetilde H^{\bullet }_R(\mathrm {pt},\Bbbk )$ -module on $\widetilde H^{\bullet }_L(X,\Bbbk )$ by

(3-3) $$ \begin{align} \tilde m\tilde b=\tilde m\cup \tilde v_A^*(\tilde b). \end{align} $$

Let us make L and R act on the products $X\times E\times \widetilde E$ and $E\times \widetilde E$ , respectively, diagonally: $l(x,e,\tilde e)=(lx,le,l\tilde e)$ and $r(e,\tilde e)=(re,r\tilde e)$ . Let $q_A$ be the map given by $L(x,e,\tilde e)\mapsto A(x)^{-1}(e,\tilde e)$ . Then we get the following diagram:

(3-4)

If we forget about the dashed arrows, then we get a commutative diagram (as the underlying diagram for sets is commutative). Therefore, the central rectangle (with the dashed arrows) is also commutative, because all slant arrows are isomorphisms. As all maps preserve the additive structure on cohomologies, it remains to check Condition (2-1): for $m\in H_L^{\bullet }(X,\Bbbk )$ and $b\in H_R^{\bullet }(\mathrm {pt},\Bbbk )$ ,

$$ \begin{align*} \mu(mb)=\mu(m\cup v_A^*(b))=\mu(m)\cup \mu v_A^*(b)=\mu(m)\cup \tilde v_A^*\iota(b)=\mu(m)\iota(b), \end{align*} $$

where we use the multiplication rules (3-2) and (3-3), and the fact that $\mu $ preserves the cup product.

Corollary 3.2 (of Lemma 3.1).

Up to isomorphism, the $H_L^{\bullet }(\mathrm {pt},\Bbbk )$ - $H^{\bullet }_R(\mathrm {pt},\Bbbk )$ - bimodule $H^{\bullet }_L(X,\Bbbk )$ is independent of the choice of E.

Proof. It suffices to prove a result similar to Lemma 3.1 for the canonical action. We can do it if in (3-4), we replace: R with L; $v_A$ and $\tilde v_A$ with the canonical projections $X\,{}_L\!\times \,E\to L\mathop {\backslash } E$ and $X\,{}_L\!\times \,\tilde E\to L\mathop {\backslash } \tilde E$ , respectively; $q_A$ with $L\mathop {\backslash }\mathop{\rm pr}\nolimits _{2,3}$ .

Remark 3.3. The above stipulation that both $E\to L\mathop {\backslash } E$ and $E\to R\mathop {\backslash } E$ are universal principal L- and R-bundles usually is the result of the fact that G is a Lie group, L and R are its closed subgroups, and the quotient map $E\to G\mathop {\backslash } E$ is a universal principal G-bundle.

Remark 3.4. If $R=L$ and $A:X\to G/L$ is defined by $A(x)=L$ for any $x\in X$ , then $v_A$ is the canonical projection. In this case, the corresponding right action (3-2) of $H^{\bullet }_L(\mathrm {pt},\Bbbk )$ on $H_L^{\bullet }(X,\Bbbk )$ is canonical.

3.2 Pull-back as a bimodule homomorphism

Keeping the notation of the previous section, let additionally Y be another L-space and $f:Y\to X$ be an L-equivariant continuous map. Then the composition $Af:Y\to G/R$ is also L-equivariant.

Lemma 3.5. The equivariant pull-back $f^{\star }:H^{\bullet }_L(X,\Bbbk )\to H^{\bullet }_L(Y,\Bbbk )$ is a homomorphism of bimodules, where the left actions are canonical and the right actions on the domain and codomain are twisted by A and $Af$ , respectively.

Proof. First, we prove the claim about the left actions. We get the following commutative diagram:

(3-5)

Let $a\in H_L^{\bullet }(\mathrm {pt},\Bbbk )$ and $m\in H^{\bullet }_L(X,\Bbbk )$ . It follows from the above diagram that

$$ \begin{align*} f^{\star}(am)=f^{\star}(\mathop{\mathbf{can}}\nolimits^*(a)\cup m)=f^{\star}\mathop{\mathbf{can}}\nolimits^*(a)\cup f^{\star}(m)=\mathop{\mathbf{can}}\nolimits^*(a)\cup f^{\star}(m)=af^{\star}(m). \end{align*} $$

Now let us deal with the right actions. It follows directly from definition that

(3-6) $$ \begin{align} v_{Af}=v_A(f\,{}_L\!\times\,\mathrm{id}). \end{align} $$

Hence, for any $m\in H^{\bullet }_L(X,\Bbbk )$ and $b\in H_R^{\bullet }(\mathrm {pt},\Bbbk )$ ,

$$ \begin{align*} f^{\star}(mb)=f^{\star}(m\cup v_A^*(b))=f^{\star}(m)\cup f^{\star} v_A^*(b)=f^{\star}(m)\cup v_{Af}^*(b)=f^{\star}(m)b.\\[-40pt] \end{align*} $$

3.3 Push-forward as a bimodule homomorphism

Suppose we are in the situation of Section 2.13, so $f\;{}_L\! \times \mathrm {id}:Y\;{}_L\! \times E^N\to X\;{}_L\! \times E^N$ is denoted by $f^N$ .

Let R be a closed subgroup of G and $A:X\to G/R$ be an L-equivariant continuous map (as in Section 3.1). We get the commutative diagrams (refer to Remark 2.8 about the notation)

(3-7)

Let $m\in H_L^n(Y,\Bbbk )$ and $b\in H_R^l(\mathrm {pt},\Bbbk )$ . For N big enough, we get by (2-5), the commutativity of diagrams (3-7), the projection formula (Proposition 2.9), and a compact version of (3-6) that

$$ \begin{align*} f_\star(mb)&=f_\star(m\cup v_{Af}^*(b))=(i_X^*)^{-1}f_*^Ni_Y^*(m\cup v_{Af}^*(b))\\ &=(i_X^*)^{-1}f_*^N(i_Y^*(m)\cup(v_{Af}i_Y)^*(b)) =(i_X^*)^{-1}f_*^N(i_Y^*(m)\cup(v^N_{Af})^*i_R^*(b))\\ &=(i_X^*)^{-1}f_*^N(i_Y^*(m)\cup (f^N)^*(v^N_A)^*i_R^*(b)) =(i_X^*)^{-1}(f_*^Ni_Y^*(m)\cup(i_Rv^N_A)^*(b))\\ &=(i_X^*)^{-1}(f_*^Ni_Y^*(m)\cup i_X^*v_A^*(b)) =(i_X^*)^{-1}f_*^Ni_Y^*(m)\cup v_A^*(b)=f_\star(m)b. \end{align*} $$

We also get the commutative diagrams

(3-8)

Suppose that the cohomology $H_L^{\bullet }(\mathrm {pt},\Bbbk )$ vanishes in odd degrees. Let $a\in H_R^{2l}(\mathrm {pt},\Bbbk )$ and $m\in H_L^n(Y,\Bbbk )$ . For N big enough, we get by (2-5), the commutativity of diagrams (3-8), the projection formula (Proposition 2.9), the graded-commutativity of the cup product, and a compact version of (3-5) that

$$ \begin{align*} f_\star(am)&=f_\star(\mathop{\mathbf{can}}\nolimits^*(a)\cup m)=(i_X^*)^{-1}f_*^Ni_Y^*(\mathop{\mathbf{can}}\nolimits^*(a)\cup m)\\ &=(i_X^*)^{-1}f_*^N((\mathop{\mathbf{can}}\nolimits i_Y)^*(a)\cup i_Y^*(m))\\ &=(i_X^*)^{-1}f_*^N(\mathop{\mathbf{can}}\nolimits^* i_L^*(a)\cup i_Y^*(m))=(i_X^*)^{-1}f_*^N((f^N)^*\mathop{\mathbf{can}}\nolimits^*i_L^*(a)\cup i_Y^*(m))\\ &=(i_X^*)^{-1}f_*^N(i_Y^*(m)\cup(f^N)^*(i_L\mathop{\mathbf{can}}\nolimits)^*(a))=(i_X^*)^{-1}(f_*^Ni_Y^*(m)\cup(\mathop{\mathbf{can}}\nolimits i_X)^*(a))\\ &=(i_X^*)^{-1}f_*^Ni_Y^*(m)\cup\mathop{\mathbf{can}}\nolimits^*(a)=\mathop{\mathbf{can}}\nolimits^*(a)\cup f_\star(m)=af_\star(m). \end{align*} $$

So we have proved the following counterpart of Lemma 3.5.

Lemma 3.6. The equivariant push-forward $f_\star :H^{\bullet }_L(Y,\Bbbk )\to H^{\bullet +\dim X-\dim Y}_L(X,\Bbbk )$ is a homomorphism of right $H_R^{\bullet }(\mathrm {pt},\Bbbk )$ -modules, where the right actions on the domain and codomain are twisted by $Af$ and A, respectively.

If, moreover, the cohomology $H_L^{\bullet }(\mathrm {pt},\Bbbk )$ vanishes in odd degrees, then $f_\star $ is a homomorphism of left $H_L^{\bullet }(\mathrm {pt},\Bbbk )$ -modules, where both left actions of $H_L^{\bullet }(\mathrm {pt},\Bbbk )$ are canonical.

3.4 The embedding of Borel constructions

We fix the setup that we preserve until the end of Section 3. Let $L,R,P,Q$ be subgroups of a topological group G such that $R\subset P$ and $Q\subset P$ . Let X and Y be topological spaces such that:

1. (i) L acts on the left on X;

2. (ii) R acts on the right on X;

3. (iii) Q acts on the left on Y.

Assuming that R and Q act on P on the left and on the right, respectively, via multiplication, we can write these data as follows:

$$ \begin{align*} L\circlearrowright X\circlearrowleft R\circlearrowright P\circlearrowleft Q\circlearrowright Y. \end{align*} $$

We also assume that:

1. (iv) the actions of L and R on X commute.

Let additionally:

1. (v) $\alpha :X\to G$ be a continuous R- and L-equivariant map.

In that case, we get the morphism of left L-spaces $A:X/R\to G/R$ given by

(3-9) $$ \begin{align} A(xR)=\alpha(x)R. \end{align} $$

Let E be a left G-space. Then we are in the situation of Section 3.1 (with X replaced by $X/R$ ) and we have the map $v_A:(X/R)\,{}_L\!\times \,E\to R\mathop {\backslash } E$ given by (3-1).

In view of item (iv), the group L acts on the left on $X\mathop {\times }\limits _R P\mathop {\times }\limits _QY$ by $ l[x:p:y]=[lx:p:y] $ . We consider the map

$$ \begin{align*} \varphi:\big(X\mathop{\times}\limits_R P\mathop{\times}\limits_QY\big)\,{}_L\times E\to((X/R)\,{}_L\times E)\times(Y\,{}_Q\times E) \end{align*} $$

defined by

(3-10) $$ \begin{align} L([x:p:y],e)\mapsto(L(xR,e),Q(y,p^{-1}\alpha(x)^{-1}e)). \end{align} $$

The reader can easily check that this map is well defined and continuous.

We get the following diagram:

(3-11)

where $\pi _R$ and $\pi _Q$ are the natural quotient maps. In general, the rectangle on the right is not commutative. However, we get the following result.

Lemma 3.7. The image of $\varphi $ is equal to $((X/R)\,{}_L\!\times \,E)\times _{\pi _R\,v_A\mathop{\rm pr}\nolimits _1=\pi _Q\mathop {\mathbf {can}}\nolimits \mathop{\rm pr}\nolimits _2}(Y\,{}_Q\!\times \,E)$ .

Proof. It follows from (3-10) that the two maximal paths of diagram (3-11) commute, that is, $\pi _R\,v_A\mathop{\rm pr}\nolimits _1\varphi =\pi _Q \mathop {\mathbf {can}}\nolimits \mathop{\rm pr}\nolimits _2\varphi $ . Thus, the image of $\varphi $ is contained in the fiber product.

Conversely, let $a=(L(xR,e),Q(y,e'))$ be an arbitrary point of the fiber product. Hence, $P\alpha (x)^{-1}e=Pe'$ . Thus, there exists an element $p\in P$ such that $pe'=\alpha (x)^{-1}e$ . We get $\varphi (L([x:p:y],e))=a$ .

Lemma 3.8. Suppose that P acts freely on E. Then $\varphi $ is an embedding.

Proof. Let $L([x:p:y],e)$ and $L([x':p':y'],e')$ be two orbits mapped to the same pair by $\varphi $ . As $L(xR,e)=L(x'R,e')$ , there exists $l\in L$ such that $lxR=x'R$ and $le=e'$ . From the first equality, it follows that there exists $r\in R$ such that $lxr=x'$ . We get

(3-12) $$ \begin{align}L([x:p:y],e)&=L([lx:p:y],le)=L([lxr:r^{-1}p:y],e') \nonumber\\ &=L([x':r^{-1}p:y],e')\mathop{\longmapsto}\limits^{\ \ {\rm pr}_2\varphi\ \ }Q(y,p^{-1}r\alpha(x')^{-1}e'). \end{align} $$

As $L([x':p':y'],e')$ is mapped by $\mathop{\rm pr}\nolimits _2\varphi $ to the same orbit,

$$ \begin{align*} Q(y,p^{-1}r\alpha(x')^{-1}e')=Q(y',(p')^{-1}\alpha(x')^{-1}e'). \end{align*} $$

Therefore, there exists $q\in Q$ such that $qy=y'$ and $qp^{-1}r\alpha (x')^{-1}e'=(p')^{-1}\alpha (x')^{-1}e'$ . From the last equality and the freeness of the action of P on E, we get $qp^{-1}r=(p')^{-1}$ . Hence, $r^{-1}p=p'q$ and, applying (3-12),

$$ \begin{align*} L([x:p:y],e)&=L([x':r^{-1}p:y],e')=L([x':p'q:y],e')\\ &=L([x':p':qy],e')=L([x':p':y'],e'), \end{align*} $$

as required.

Theorem 3.9. Suppose that the quotient map $E\to P\mathop {\backslash } E$ is a principal P-bundle. Then $\varphi $ is a topological embedding.

Proof. We denote this quotient map by $\pi $ and by D the fiber product from the formulation of Lemma 3.7. Let a be any point of D. The assumption of this lemma implies that there exists an open neighborhood $U\subset P\mathop {\backslash } E$ of the point $\pi _Rv_A\mathop{\rm pr}\nolimits _1(a)=\pi _Q\mathop {\mathbf {can}}\nolimits \mathop{\rm pr}\nolimits _2(a)$ and a P-equivariant homeomorphism $h:P \times U\stackrel \sim \to \pi ^{-1}(U)$ such that the diagram

is commutative. We set $\mathbf p=\mathop{\rm pr}\nolimits _1 h^{-1}$ . Clearly, $\mathbf p(pe)=p\mathbf p(e)$ for any $p\in P$ and ${e\in \pi ^{-1}(U)}$ .

We define the continuous function

$$ \begin{align*} \xi:(\pi_Rv_A)^{-1}(U)\times(\pi_Q\mathop{\mathbf{can}}\nolimits)^{-1}(U)\to (X\mathop{\times}\limits_R P\mathop{\times}\limits_QY)\,{}_L\!\times\,E \end{align*} $$

as follows. Let $d=(L(xR,e),Q(y,e'))$ be a point of the domain of $\xi $ . We set

$$ \begin{align*} \xi(d)=L([x:\mathbf p(\alpha(x)^{-1}e)\mathbf p(e')^{-1}:y],e). \end{align*} $$

One can easily check that this definition does not depend on the choice of $x,y,e,e'$ in the representation of d.

Now suppose that $d\in D$ . Then we get $P\alpha (x)^{-1}e=Pe'$ . Let us write $\alpha (x)^{-1}e=pe'$ for the corresponding $p\in P$ . We get

$$ \begin{align*} \varphi\xi(d)&=(L(xR,e),Q(y ,\mathbf p(e')\mathbf p(\alpha(x)^{-1}e)^{-1}\alpha(x)^{-1}e))\\ &=(L(xR,e),Q(y ,\mathbf p(e')\mathbf p(pe')^{-1}pe'))\\ &=(L(xR,e),Q(y ,\mathbf p(e')\mathbf p(e')^{-1}p^{-1}pe')) =(L(xR,e),Q(y ,e'))=d. \end{align*} $$

This calculation proves that the restriction of $\xi $ to $(\pi _Rv_A)^{-1}(U)\times (\pi _Q\mathop {\mathbf {can}}\nolimits )^{-1}(U)\cap D$ inverts $\varphi $ . As a belongs to the last subset, all such subsets cover D. Thus, the required claim follows from Lemma 3.8 and Proposition 2.1.

3.5 Canonical and twisted projections for the triple product

By (3-10), we get the following commutative diagram:

(3-13)

Now let M be a subgroup of G and $B:Y\to G/M$ be a Q-equivariant continuous map. We consider the map $\alpha B:X\mathop {\times }\limits _R P\mathop {\times }\limits _Q Y\to G/M$ given by

(3-14) $$ \begin{align} [x:p:y]\mapsto \alpha(x)p B(y). \end{align} $$

It is easy to check that this map is well defined, continuous, and L-equivariant. By (3-10), we get the following commutative diagram:

(3-15)

3.6 The difference

In this section, we want to study the difference

$$ \begin{align*} ((X/R)\,{}_L\!\times\,E)\times(Y\,{}_Q\!\times\,E)-\mathop{\rm im}\varphi. \end{align*} $$

To this end, we claim some additional properties of E.

Lemma 3.10. Suppose that P acts freely on E. Let U be a compact Lie group acting continuously on E on the right so that this action and the left action of G commute. Suppose that the space $R\mathop {\backslash } E$ is Hausdorff and is acted upon by U transitively. Then the projection to the first component

$$ \begin{align*} \omega:((X/R)\,{}_L\!\times\,E)\times(Y\,{}_Q\!\times\,E)-\mathop{\rm im}\varphi\to(X/R)\,{}_L\!\times\,E \end{align*} $$

is a fiber bundle with fiber homeomorphic to

$$ \begin{align*} F_{\bar e}=\{Q(y,e)\in Y\,{}_Q\!\times\,E\mathbin{\rm |} \bar e\ne Pe\}=Y\,{}_Q\!\times\,E-(\pi_Q\mathop{\mathbf{can}}\nolimits)^{-1}(\bar e), \end{align*} $$

where $\bar e$ is an arbitrary point of $P\mathop {\backslash } E$ .

Proof. We denote the action of U by $\cdot $ . We make U act on $Y\,{}_Q\!\times \,E$ on the right by the rule $Q(y,e)\cdot u=Q(y,e\cdot u)$ . Then we obviously get $F_{\bar e}\cdot u=F_{\bar e\cdot u}$ . As U acts transitively on $R\mathop {\backslash } E$ , it also acts transitively on $P\mathop {\backslash } E$ . Therefore, the spaces $F_{\bar e}$ are homeomorphic for different points $\bar e$ . We rely on the notation of Diagram (3-11).

Let $a\in (X/R)\,{}_L\!\times \,E$ be an arbitrary point. By Lemma 3.8,

$$ \begin{align*} \omega^{-1}(a)=\{a\}\times F_{\pi_Rv_A(a)}\cong F_{\pi_Rv_A(a)}\cong F_{\bar e}. \end{align*} $$

We consider the map $t:U\to R\mathop {\backslash } E$ defined by $t(u)=v_A(a)u$ . Let V be the stabilizer of $v_A(a)$ in U. Note that V is a Lie group as it is closed in U. Let us consider the commutative diagram

The bottom map, which is given by $Vu\mapsto v_A(a)\cdot u$ , is continuous and bijective. It is a homeomorphism, being a map from a compact space to a Hausdorff space. As the natural projection $U\to V\mathop {\backslash } U$ is a principal V-bundle, it has a continuous section in an open neighborhood of any point of $V\mathop {\backslash } U$ . From the diagram above, we get the same property for the map t. In particular, there exist an open neighborhood W of $v_A(a)$ in $R\mathop {\backslash } E$ and a continuous section $s:W\to U$ of t. In other words,

(3-16) $$ \begin{align} w=t(s(w))=v_A(a)\cdot s(w) \end{align} $$

for any $w\in W$ .

Let $H=v_A^{-1}(W)$ . It is an open subset of $(X/R)\,{}_L\!\times \,E$ containing a. We construct the map $\sigma :H\times \omega ^{-1}(a)\to ((X/R)\,{}_L\!\times \,E)\times (Y\,{}_Q\!\times \,E)$ by

$$ \begin{align*} (h,(a,Q(y,e)))\mapsto(h,Q(y,e\cdot sv_A(h))). \end{align*} $$

This map is obviously well defined and continuous. Let us prove that $\mathop{\rm im}\sigma \cap \mathop{\rm im}\varphi =\varnothing $ . By Lemma 3.8, we have to prove the inequality

(3-17) $$ \begin{align} \pi_Rv_A(h)\ne\pi_Q( Qe\cdot sv_A(h) )=Pe\cdot sv_A(h). \end{align} $$

As the G- and U-actions on E commute, the map $\pi _R$ is U-equivariant. Therefore, (3-17) is equivalent to

$$ \begin{align*} \pi_R(v_A(h)\cdot sv_A(h)^{-1})\ne Pe. \end{align*} $$

Applying (3-16) for $w=v_A(h)$ , to compute the left-hand side, we get the equivalent inequality

$$ \begin{align*} \pi_Rv_A(a)\ne Pe, \end{align*} $$

which holds by Lemma 3.8, as $(a,Q(y,e))\notin \mathop{\rm im}\varphi $ . Thus, we can consider $\sigma $ as a continuous map from $H\times \omega ^{-1}(a)$ to $\omega ^{-1}(H)$ . The diagram

is obviously commutative.

To prove that $\sigma $ is a homeomorphism, we notice that its inverse map ${\omega ^{-1}(H)\to H\times \omega ^{-1}(a)}$ is given by

$$ \begin{align*} (h, Q(y,e) )\mapsto(h,(a,Q(y,e\cdot sv_A(h)^{-1}))).\\[-35pt] \end{align*} $$

To establish the required cohomological properties of the compact version of $F_{\bar e}$ (Lemma 4.8), we need the following result whose proof we leave to the reader.

Lemma 3.11. Suppose that the quotient map $E\to P\mathop {\backslash } E$ is a principal P-bundle. Then the composition

is a fiber bundle with fiber $Y\,{}_Q\times P$ .

3.7 The tensor product

The above results can be applied to equivariant cohomologies. Let us suppose that all quotient maps $E\to L\mathop {\backslash } E$ , $E\to P\mathop {\backslash } E$ , $E\to R\mathop {\backslash } E$ , $E\to Q\mathop {\backslash } E$ , $E\to M\mathop {\backslash } E$ are universal principal bundles for the respective groups. We denote by $\Theta $ the following composition:

(3-18)

The map $\times $ is the cross product and is given by $a\otimes b\mapsto \mathop{\rm pr}\nolimits _1^*(a)\cup \mathop{\rm pr}\nolimits _2^*(b)$ . The classical rule

(3-19) $$ \begin{align} (m\otimes n)(m'\otimes n')=(-1)^{ij}(m\cup m')\otimes(n\cup n')\end{align} $$

makes $H^{\bullet }_L(X/R,\Bbbk )\,{\otimes }_{\Bbbk }\, H^{\bullet }_Q(Y,\Bbbk )$ into an associative ring.

Using the notation of Section 3.5, we can get the following result.

Theorem 3.12. The map $\Theta $ is a homomorphism of rings and of left $H^{\bullet }_L(\mathrm {pt},\Bbbk )$ -modules with respect to the canonical actions. For any Q-equivariant continuous map $B:Y\to G/M$ , the map $\Theta $ is also a homomorphism of right $H^{\bullet }_M(\mathrm {pt},\Bbbk )$ -modules with respect to the actions twisted by B and $\alpha B$ on the domain and the codomain of $\Theta $ , respectively.

Proof. The fact that $\Theta $ is a homomorphism of rings can be proved following the calculation before [Ha, Theorem 3.16].

Let $a\in H^{\bullet }_L(\mathrm {pt},\Bbbk )$ , $m\in H^{\bullet }_L(X/R,\Bbbk )$ , and $n\in H^{\bullet }_Q(Y,\Bbbk )$ . As diagram (3-13) is commutative,

$$ \begin{align*} \Theta( a m\otimes n)&=\Theta((\mathop{\mathbf{can}}\nolimits^*( a)\cup m)\otimes n)=\varphi^*(\mathop{\rm pr}\nolimits_1^*(\mathop{\mathbf{can}}\nolimits^*( a)\cup m)\cup\mathop{\rm pr}\nolimits_2^*( n))\\ &=(\mathop{\mathbf{can}}\nolimits\mathop{\rm pr}\nolimits_1\varphi)^*( a)\cup\varphi^*(\mathop{\rm pr}\nolimits_1^*( m)\cup\mathop{\rm pr}\nolimits_2^*( n))\\&=\mathop{\mathbf{can}}\nolimits^*( a)\cup\Theta( m\otimes n) = a\Theta( m\otimes n). \end{align*} $$

Now let $ m\in H^{\bullet }_L(X/R,\Bbbk )$ , $ n\in H^{\bullet }_Q(Y,\Bbbk )$ , and $b\in H^{\bullet }_M(\mathrm {pt},\Bbbk )$ . As diagram (3-15) is commutative,

$$ \begin{align*} \Theta( m\otimes nb)&=\Theta( m\otimes (n\cup v_B^*(b)))=\varphi^*(\mathop{\rm pr}\nolimits_1^*( m)\cup\mathop{\rm pr}\nolimits_2^*( n\cup v_B^*(b)))\\ &=\varphi^*(\mathop{\rm pr}\nolimits_1^*( m)\cup \mathop{\rm pr}\nolimits_2^*( n))\cup (v_B\mathop{\rm pr}\nolimits_2\varphi)^*(b)\\ &=\Theta( m\otimes n)\cup v_{\alpha B}^*(b) =\Theta( m\otimes n)b.\\[-42pt] \end{align*} $$

Now let us look more closely at the tensor product $H^{\bullet }_L(X/R,\Bbbk )\,{\otimes }_{\Bbbk }\, H^{\bullet }_Q(Y,\Bbbk )$ . According to Section 3.1, the left factor $H^{\bullet }_L(X/R,\Bbbk )$ is a right $H_R^{\bullet }(\mathrm {pt},\Bbbk )$ -module with the action twisted by A. However, the right factor $H^{\bullet }_Q(Y,\Bbbk )$ is a left $H_Q^{\bullet }(\mathrm {pt},\Bbbk )$ -module with respect to the canonical action (Section 2.7). Moreover, the quotient maps $\pi _R$ and $\pi _Q$ , refer to Diagram (3-11), yield the following maps:

$$ \begin{align*} \pi_R^*:H_P^{\bullet}(\mathrm{pt},\Bbbk)\to H_R^{\bullet}(\mathrm{pt},\Bbbk),\quad \pi_Q^*:H_P^{\bullet}(\mathrm{pt},\Bbbk)\to H_Q^{\bullet}(\mathrm{pt},\Bbbk). \end{align*} $$

They allow us to define the structure of a right $H_P^{\bullet }(\mathrm {pt},\Bbbk )$ -module on $H^{\bullet }_L(X/R,\Bbbk )$ and of a left $H_P^{\bullet }(\mathrm {pt},\Bbbk )$ -module on $H^{\bullet }_Q(Y,\Bbbk )$ .

Lemma 3.13. The map $\Theta $ factors through $H^{\bullet }_L(X/R,\Bbbk )\otimes _{H_P^{\bullet }(\mathrm {pt},\Bbbk )}H^{\bullet }_Q(Y,\Bbbk )$ .

Proof. Let $m\in H^{\bullet }_L(X/R,\Bbbk )$ , $n\in H^{\bullet }_Q(Y,\Bbbk )$ , and $a\in H_P^{\bullet }(\mathrm {pt},\Bbbk )$ . By Lemma 3.7 and Diagram (3-18) defining $\Theta $ ,

$$ \begin{align*} \Theta(m a\otimes n)&=\Theta(m\pi_R^*( a)\otimes n)=\Theta(m\cup v_A^*\pi_R^*( a)\otimes n) =\varphi^*(\mathop{\rm pr}\nolimits_1^*(m\cup v_A^*\pi_R^*( a))\cup\mathop{\rm pr}\nolimits_2^*( n))\\ &=\varphi^*\mathop{\rm pr}\nolimits_1^*(m)\cup (\pi_R v_A \mathop{\rm pr}\nolimits_1 \varphi)^*( a)\cup\varphi^*\mathop{\rm pr}\nolimits_2^*( n)\\ &=\varphi^*\mathop{\rm pr}\nolimits_1^*(m)\cup (\pi_Q \mathop{\mathbf{can}}\nolimits \mathop{\rm pr}\nolimits_2\varphi)^*( a)\cup\varphi^*\mathop{\rm pr}\nolimits_2^*( n)\\ &=\varphi^*(\mathop{\rm pr}\nolimits_1^*(m)\cup \mathop{\rm pr}\nolimits_2^* \mathop{\mathbf{can}}\nolimits^* \pi_Q^*( a)\cup\mathop{\rm pr}\nolimits_2^*( n)) =\varphi^*(\mathop{\rm pr}\nolimits_1^*(m)\cup \mathop{\rm pr}\nolimits_2^*(\mathop{\mathbf{can}}\nolimits^* \pi_Q^*( a)\cup n))\\ &=\Theta(m\otimes \mathop{\mathbf{can}}\nolimits^*\pi_Q^*( a)\cup n)=\Theta(m\otimes \pi_Q^*( a) n)=\Theta(m\otimes a n).\\[-42pt] \end{align*} $$

We denote the map induced by $\Theta $ as follows:

$$ \begin{align*} \theta:H^{\bullet}_L(X/R,\Bbbk)\otimes_{H_P^{\bullet}(\mathrm{pt},\Bbbk)}H^{\bullet}_Q(Y,\Bbbk)\to H_L^{\bullet}(X\mathop{\times}\limits_R P\mathop{\times}\limits_Q Y,\Bbbk). \end{align*} $$

We make the left-hand side into a ring using product (3-19).

Corollary 3.14. The map $\theta $ is a homomorphism of rings and of left $H^{\bullet }_L(\mathrm {pt},\Bbbk )$ - modules with respect to the canonical actions. For any Q-equivariant continuous map ${B:Y\to G/M}$ , the map $\theta $ is also a homomorphism of right $H^{\bullet }_M(\mathrm {pt},\Bbbk )$ -modules with respect to the actions twisted by B and $\alpha B$ on the domain and the codomain of $\theta $ , respectively.

Proof. The result follows from Theorem 3.12.

4 The isomorphism

We prove that the map $\theta $ introduced in Section 3 is an isomorphism under certain restrictions, which we are going to formulate. First, we assume the following two conditions:

1. (I) the ring $\Bbbk $ has finite global dimension $\mathop {\mathrm {gld}}(\Bbbk )$ ;

2. (II) G is a compact Lie group and L, R, P, Q, M are closed subgroups.

These conditions are supposed to hold for the rest of the paper.

4.1 Künneth formula

Let $X_1,\ldots ,X_m$ be topological spaces such that $H^n(X_j,\Bbbk )$ are free of finite rank for all $n\leqslant N$ and $j=2,\ldots ,m$ . Then for any $n\leqslant N-\mathop {\mathrm {gld}}(\Bbbk )$ , we have the isomorphism

$$ \begin{align*} \bigoplus_{i_1+\cdots+i_m=n}H^{i_1}(X_1,\Bbbk)\otimes\cdots\otimes H^{i_m}(X_m,\Bbbk)\stackrel\sim\to H^n(X_1\times\cdots\times X_m,\Bbbk) \end{align*} $$

that is given by the cross product $a_1\otimes \cdots \otimes a_m\mapsto p_1^*(a_1)\cup \cdots \cup p_m^*(a_m)$ .

This isomorphism and Proposition 2.4 prove that $H^n((E^N)^m,\Bbbk )=0$ for any ${0<n\leqslant 2(N-{\mathfrak n}_{G})}$ and natural number m. Moreover, the space $E^m$ is contractible. Hence, we get the following result similar to Proposition 2.6.

Proposition 4.1. Suppose that for each $i=1,\ldots ,m$ , there is a left $L^{(i)}$ -space $X^{(i)}$ for a closed subgroup $L^{(i)}$ of G. Then the restriction map

$$ \begin{align*} H^n((X^{(1)}&\,{}_{L^{(1)}}\!\times E)\times\cdots\times(X^{(m)}\,{}_{L^{(m)}}\!\times E),\Bbbk)\\&\to H^n((X^{(1)}\,{}_{L^{(1)}}\!\times E^N)\times\cdots\times(X^{(m)}\,{}_{L^{(m)}}\!\times E^N),\Bbbk) \end{align*} $$

is an isomorphism for $n\leqslant 2(N-{\mathfrak n}_{G})$ .

4.2 An auxiliary lemma

We are going to use the following result proved in [S2, Lemma 18].

Proposition 4.2. Let S be a locally compact Hausdorff space, $p:S\to T$ be a fiber bundle with fiber F, $t\in T$ be a point, and $\Bbbk $ be a commutative ring. Suppose that T is compact, Hausdorff, connected, and simply connected, all $H_c^n(F,\Bbbk )$ are free of finite rank, $H_c^n(F,\Bbbk )=0$ for odd n, and $H_c^n(T,\Bbbk )=0$ for odd $n\leqslant N$ .

Then the following are true.

1. (1) The restriction map $H_c^n(S,\Bbbk )\to H_c^n(p^{-1}(t),\Bbbk )$ is surjective for all $n<N$ .

2. (2) $H_c^n(S-p^{-1}(t),\Bbbk )=0$ for odd $n<N$ .

3. (3) If $H_c^n(T,\Bbbk )$ are free of finite rank for $n\leqslant N$ , then the $\Bbbk $ -modules $H_c^n(S-p^{-1}(t),\Bbbk )$ are also free of finite rank for $n<N$ .

4.3 Leray spectral sequence with compact support

For any topological space S and a commutative ring $\Bbbk $ , we denote by the constant sheaf on S. In the formulation of the next result (refer, for example, to [Di, Corollary 2.3.24]), we use the direct image functor $f_!$ with compact (proper) support for a continuous map f between locally compact spaces and its qth right derived functor $R^q\!f_!$ [KS, II.2.5, II.2.6].

Proposition 4.3. Let $f:S\to T$ be a continuous map between locally compact Hausdorff spaces. There exists a first quadrant spectral sequence with the second page converging to $H_c^{p+q}(S,\Bbbk )$ .

Let us consider the case where $f:S\to T$ is a fiber bundle with fiber F. In this case, the sheaf is locally constant. Indeed, applying the proper base change [KS, Proposition 2.6.7], we reduce the problem to the case where $S=F\times T$ and $f=\mathop{\rm pr}\nolimits _2$ . Applying the proper base change to the Cartesian square

we get

Taking the qth cohomology,

(4-1)

Corollary 4.4. Let $f:S\to T$ be a fiber bundle with fiber F, where S and T are locally compact and Hausdorff. Suppose that $H^q_c(F,\Bbbk )$ is free of finite rank for any q and T is simply connected. Then there exists a first quadrant spectral sequence with the second page $E_2^{p,q}=H_c^p(T,\Bbbk )\,{\otimes }_{\Bbbk }\, H^q_c(F,\Bbbk )$ converging to $H_c^{p+q}(S,\Bbbk )$ .

In particular, if $H_c^{\bullet }(T,\Bbbk )$ and $H^{\bullet }_c(F,\Bbbk )$ are free of finite rank in each degree and vanish in odd degrees, then $ H_c^{\bullet }(S,\Bbbk )\cong H_c^{\bullet }(T,\Bbbk )\,{\otimes }_{\Bbbk }\, H^{\bullet }_c(F,\Bbbk ) $ .

Proof. By the preceding arguments, we know that the sheaf is locally constant. It follows from [I, Proposition IV.4.20] that is constant. Thus, by (4-1), it is isomorphic to , where n is the rank of $H^q_c(F,\Bbbk )$ . To prove the first result, it suffices to substitute this sheaf into the spectral sequence of Proposition 4.3.

The second result follows from the fact that this spectral sequence collapses at the second page and $\mathop {\rm Ext}^1(\Bbbk ,M)=0$ for any $\Bbbk $ -module M.

Corollary 4.5. Let L be a connected compact Lie group such that $H^{\bullet }_L(\mathrm {pt},\Bbbk )$ is free of finite rank in each degree and vanishes in odd degrees. For any compact Hausdorff L-space X such that $H^{\bullet }(X,\Bbbk )$ is free of finite rank in each degree and vanishes in odd degrees, there is an isomorphism $ H^{\bullet }_L(X,\Bbbk )\cong H^{\bullet }_L(\mathrm {pt},\Bbbk )\,{\otimes }_{\Bbbk }\, H^{\bullet }(X,\Bbbk ) $ .

Proof. We assume that $G=L$ and the spaces $E^N$ are chosen as in Section 2.8. Let n be a nonnegative integer. We choose any N such that $n<2(N-{\mathfrak n}_{G})$ . Applying Corollary 4.4 together with Corollary 2.5 to the canonical projection ${X\,{}_L\!\times \,E^N\to L\mathop {\backslash } E^N}$ , we get the spectral sequence with the following second page: $ E_2^{p,q}=H^p(L\mathop {\backslash } E^N,\Bbbk )\,{\otimes }_{\Bbbk }\, H^q(X,\Bbbk ) $ . By Proposition 2.6, we get that $ {E_2^{p,q}=H_L^p(\mathrm {pt},\Bbbk )\,{\otimes }_{\Bbbk }\, H^q(X,\Bbbk ) }$ for $p\leqslant 2(N-{\mathfrak n}_{G})$ . The differentials coming to and from each $E_r^{p,q}$ for $p+q<2(N-{\mathfrak n}_{G})$ are zero. Therefore, $E_\infty ^{p,q}=E_2^{p,q}$ . As no extension problem emerges in this case,

$$ \begin{align*} H^n(X\,{}_L\!\times\,E^N)=\bigoplus_{p+q=n}H_L^p(\mathrm{pt},\Bbbk)\,{\otimes}_{\Bbbk}\, H^q(X,\Bbbk) \end{align*} $$

for $n<2(N-{\mathfrak n}_{G})$ . Proposition 2.6 applied to the left-hand side finishes the proof.

4.4 Restrictions on groups and spaces

We consider the following additional conditions:

1. (III) P, Q, and L are connected;

2. (IV) $H^n_P(\mathrm {pt},\Bbbk )$ , $H^n_Q(\mathrm {pt},\Bbbk )$ , and $H^n_L(\mathrm {pt},\Bbbk )$ are free of finite rank and vanish for odd n;

3. (V) X and Y are compact and Hausdorff;

4. (VI) the cohomologies of $X/R$ , $P/Q$ , and Y with coefficients in $\Bbbk $ are free of finite rank in each degree and vanish in odd degrees;

5. (VII) $X/R$ and $P/Q$ are simply connected;

6. (VIII) the quotient map $X\to X/R$ is a principal R-bundle.

By Proposition 2.2 and Condition (VIII), these conditions imply that the natural projections

$$ \begin{align*} P\mathop{\times}\limits_Q Y\to P/Q,\quad X\mathop{\times}\limits_R P\mathop{\times}\limits_Q Y\to X/R \end{align*} $$

are fiber bundles with fibers Y and $P\mathop {\times }\limits _Q Y$ , respectively. These projections are given by $[p:y]\mapsto pQ$ and $[x:p:y]\mapsto xR$ . To apply Proposition 2.2, we can consider the isomorphisms $P\mathop {\times }\limits _Q Y\cong Y\,{}_Q\!\times P$ and $X\mathop {\times }\limits _R P\mathop {\times }\limits _Q Y\cong (P\mathop {\times }\limits _Q Y)\,{}_R\!\times X$ given by $[p:y]\mapsto Q(y,p^{-1})$ and $[x:p:y]\mapsto R([p:y],x)$ , respectively. Here we consider X as a left R-space under the following action: $rx=xr^{-1}$ . We also have the isomorphisms $R\mathop {\backslash } X\cong X/R$ and $Q\mathop {\backslash } P\cong P/Q$ given by $Rx\mapsto xR$ and ${Qp\mapsto p^{-1}Q}$ , respectively. Our projections become canonical in the sense of Section 2.4 if we apply the identifications described just above. By Conditions (II) and (V), we get that all four spaces in the left- and right-hand sides of the above formulas are compact and Hausdorff. Applying Corollary 4.4 to the first sequence and using Conditions (VI) and (VII),

$$ \begin{align*} H^{\bullet}(P\mathop{\times}\limits_Q Y,\Bbbk)\cong H^{\bullet}(P/Q,\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(Y,\Bbbk). \end{align*} $$

Hence, we also get that the cohomology in the left-hand side vanishes in odd degrees and is free of finite rank in each degree. Now applying Corollary 4.4 to the second sequence and using Conditions (VI) and (VII) again,

(4-2) $$ \begin{align}H^{\bullet}(X\mathop{\times}\limits_R P\mathop{\times}\limits_Q Y,\Bbbk)&\cong H^{\bullet}(X/R,\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(P\mathop{\times}\limits_Q Y,\Bbbk)\nonumber\\&\cong H^{\bullet}(X/R,\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(P/Q,\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(Y,\Bbbk). \end{align} $$

This cohomology also vanishes in odd degrees and is free of finite rank in each degree.

Lemma 4.6. The space $(X/R)\,{}_L\!\times \,E^N$ is simply connected.

Proof. By Proposition 2.2, $(X/R)\,{}_L\!\times \,E^N\to L\mathop {\backslash } E^N$ is a fiber bundle with fiber $X/R$ . Therefore, the result follows from Condition (VII) and the long exact sequence of homotopy groups

$$ \begin{align*} \{1\}=\pi_1(X/R)\to \pi_1((X/R)\,{}_L\!\times\,E^N)\to \pi_1(L\mathop{\backslash} E^N)=\{1\}. \end{align*} $$

The last equality follows from Corollary 2.5.

4.5 Surjectivity

We use here the abbreviations (refer to Remark 2.8)

$$ \begin{align*} Z=X\mathop{\times}\limits_R P\mathop{\times}\limits_Q Y,\quad C^N=((X/R)\,{}_L\!\times\,E^N)\times(Y\,{}_Q\!\times\,E^N)-\mathop{\rm im}\varphi^N. \end{align*} $$

Lemma 4.7. $H^n((X/R)\;{}_L\!\times E^N,\Bbbk )=H^n(Z\;{}_L\!\times E^N,\Bbbk )=0$ for odd $n\leqslant 2(N-{\mathfrak n}_{G})$ .

Proof. The result follows from Proposition 2.6, Conditions (III), (IV), (VI), (4-2), and Corollary 4.5.

We are going to study the cohomologies with compact support of the spaces $C^N$ . First, we study the cohomology of the fiber $F^N_{\bar e}$ ; refer to Lemma 3.10 and Remark 2.8.

Lemma 4.8. For any $n<2(N-{\mathfrak n}_{G})$ and $\bar e\in P\mathop {\backslash } E^N$ , the cohomology $H_c^n(F^N_{\bar e},\Bbbk )$ is free of finite rank and vanishes if n is odd.

Proof. It suffices to apply Parts (2) and (3) of Proposition 4.2 to the fiber bundle $\pi _Q\mathop {\mathbf {can}}\nolimits :Y\,{}_Q\!\times \,E^N\to P\mathop {\backslash } E^N$ with fiber $Y\,{}_Q\times P\cong P\mathop {\times }\limits _Q Y$ ; refer to Lemma 3.11.

Lemma 4.9. $H_c^n(C^N,\Bbbk )=0$ for odd $n<2(N-{\mathfrak n}_{G})$ .

Proof. In view of Lemmas 4.6 and 4.8, we can apply Corollary 4.4 to the projection $\omega ^N$ as in Lemma 3.10 (refer to Remark 2.8 about the notation). The second page of this spectral sequence is equal to

$$ \begin{align*} E_2^{p,q}=H^p((X/R)\,{}_L\!\times\,E^N,\Bbbk)\,{\otimes}_{\Bbbk}\, H_c^q(F^N_{\bar e},\Bbbk) \end{align*} $$

if $q<2(N-{\mathfrak n}_{G})$ . It follows from Lemmas 4.7 and 4.8 that $E_r^{p,q}=0$ for any finite $r\geqslant 2$ if $p+q<2(N-{\mathfrak n}_{G})$ and either of p or q is odd. Thus, this fact is also true for $r=\infty $ .

Corollary 4.10. For any $n<2(N-{\mathfrak n}_{G})-1$ , the map

is surjective.

Proof. By Theorem 3.9, we get the exact sequence

Now the result follows from Lemmas 4.7 and 4.9.

Corollary 4.11. The map $\theta $ is surjective.

Proof. Under our assumption (VI), the left map (cross product) in (3-18) is an isomorphism by the Künneth formula. Therefore, it suffices to prove that $\varphi ^*$ is surjective. In each degree, this fact follows from Corollary 4.10 and Proposition 4.1 for N big enough.

Lemma 4.12. In each degree, the homomorphism $\theta $ induces a map between free $\Bbbk $ -modules of the same finite rank.

Proof. As is noted in [J, 1.5(3)], we have $H_P^{\bullet }(P/Q,\Bbbk )\cong H_Q(\mathrm {pt},\Bbbk )$ . Then the result follows from the following computation based on (4-2) and Corollary 4.5:

$$ \begin{align*} &H^{\bullet}_L(X/R,\Bbbk)\otimes_{H_P^{\bullet}(\mathrm{pt},\Bbbk)}H^{\bullet}_Q(Y,\Bbbk)\\&\quad\cong H_L^{\bullet}(X/R,\Bbbk)\otimes_{H_P^{\bullet}(\mathrm{pt},\Bbbk)}H_Q^{\bullet}(\mathrm{pt},\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(Y,\Bbbk)\\ &\quad\cong H_L^{\bullet}(X/R,\Bbbk)\otimes_{H_P^{\bullet}(\mathrm{pt},\Bbbk)}H^{\bullet}_P(\mathrm{pt},\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(P/Q,\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(Y,\Bbbk)\\ &\quad\cong H_L^{\bullet}(X/R,\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(P/Q,\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(Y,\Bbbk)\\ &\quad\cong H_L^{\bullet}(\mathrm{pt},\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(X/R,\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(P/Q,\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(Y,\Bbbk)\\ &\quad\cong H_L^{\bullet}(\mathrm{pt},\Bbbk)\,{\otimes}_{\Bbbk}\, H^{\bullet}(X\mathop{\times}\limits_R P\mathop{\times}\limits_Q Y,\Bbbk)\cong H_L^{\bullet}(X\mathop{\times}\limits_R P\mathop{\times}\limits_Q Y,\Bbbk).\\[-43pt] \end{align*} $$

To prove the main result of this section, let us remember the following proposition.

Proposition 4.13 [R, Theorem 3.6].

Let R be a commutative ring and let M be a finitely generated R-module. If $\beta :M\to M$ is an epic R-module homomorphism, then $\beta $ is an isomorphism.

Theorem 4.14. Suppose that Conditions (I)–(VIII) are satisfied. Then $\theta $ is an isomorphism of rings and left $H^{\bullet }_L(\mathrm {pt},\Bbbk )$ -modules. If M is another closed subgroup of G and $B:Y\to G/M$ is a Q-equivariant continuous map, then $\theta $ is an isomorphism of rings and $H^{\bullet }_L(\mathrm {pt},\Bbbk )$ - $H^{\bullet }_M(\mathrm {pt},\Bbbk )$ -bimodules.

Proof. Working in one degree at a time and composing $\theta $ with the isomorphism of Lemma 4.12, we get a surjective homomorphism from a finitely generated $\Bbbk $ -module to itself. Now it suffices to apply Proposition 4.13 to prove that $\theta $ is bijective. The remaining claims follow from Corollary 3.14.

We consider below two basic examples of how this theorem can be applied.

4.6 Equivariant cohomology of the flag variety

Let G be a semisimple compact Lie group and K be a maximal torus in G (as in Section 2.14).

Suppose that the order $|W|$ of the Weyl group is invertible in $\Bbbk $ . The map ${\pi _K:K\mathop {\backslash } E\to G\mathop {\backslash } E}$ given by $\pi _K(Ke)=Ge$ induces the isomorphism

(4-3) $$ \begin{align} \pi_K^*:H^{\bullet}_G(\mathrm{pt},\Bbbk)\stackrel\sim\to H_K^{\bullet}(\mathrm{pt},\Bbbk)^W, \end{align} $$

where the right-hand side is the subring of W-invariants (refer to the proof of [Br, Proposition 1]).

We are going to apply the results of the previous sections to the following data $X=G$ , $Y=G/K$ , $P=R=Q=G$ , $L=M=K$ , letting $\alpha :X\to G$ and $B:Y\to G/M$ be the identity maps on G and $G/K$ , respectively. The induced map $A:X/R\to G/R$ is then the identity map on $G/G$ . By Theorem 4.14, Condition (IV) being guaranteed by (4-3), and the calculation of $H_K^{\bullet }(\mathrm {pt},\Bbbk )$ , the homomorphism $\theta $ is an isomorphism and

$$ \begin{align*} H^{\bullet}_K(G\mathop{\times}\limits_GG\mathop{\times}\limits_G G/K,\Bbbk)\cong H_K^{\bullet}(G/G,\Bbbk)\otimes_{H^{\bullet}_G(\mathrm{pt},\Bbbk)}H_G^{\bullet}(G/K,\Bbbk). \end{align*} $$

As $G/G\cong \mathrm {pt}$ and the map $v_B:(G/K)\,{}_G\!\times \,E\to K\mathop {\backslash } E$ is a homeomorphism [J, 1.5], we get by (4-3) the well-known isomorphism of rings and bimodules

$$ \begin{align*} H^{\bullet}_K(G/K,\Bbbk)\cong H_K^{\bullet}(\mathrm{pt},\Bbbk)\otimes_{H^{\bullet}_K(\mathrm{pt},\Bbbk)^W}H_K^{\bullet}(\mathrm{pt},\Bbbk) \end{align*} $$

with the canonical action of $H_K^{\bullet }(\mathrm {pt},\Bbbk )$ on the left and on the right.

4.7 Standard bimodules

We continue to work here with the same groups G and K as in the previous section. Let us denote

(4-4) $$ \begin{align} {\mathcal R}=H^{\bullet}_K(\mathrm{pt},\Bbbk). \end{align} $$

This is the ${\mathcal R}$ - ${\mathcal R}$ -bimodule with respect to the cup product. For any $w\in W$ , we denote by ${\mathcal R}_w$ the ${\mathcal R}$ - ${\mathcal R}$ -bimodule equal to ${\mathcal R}$ as an abelian group whose left action $\cdot $ is untwisted and right action $\cdot _w$ is twisted by w:

$$ \begin{align*} r'\cdot r=r'r,\quad r\cdot_w r"=rw(r"). \end{align*} $$

The construction of this bimodule naturally arises as a special case of the twisted action described in Section 3.1. Indeed, let $A_w:\mathrm {pt}\to G/K$ be the map with the value $wK$ . Then we get the map $v_{A_w}:K\mathop {\backslash } E\cong \mathrm {pt}\,{}_K\!\times \,E\to K\mathop {\backslash } E$ , which coincides with the map $K\mathop {\backslash } \rho _{w^{-1}}$ described in Section 2.14. By (2-8), we get that the right action on $H_K^{\bullet }(\mathrm {pt},\Bbbk )$ on itself twisted by $A_w$ coincides with $\cdot _w$ .

Now let us compute the tensor product of these bimodules with the help of the isomorphism $\theta $ . Let $X=K$ , $Y=\mathrm {pt}$ , $L=R=P=Q=N=M=K$ , and $\alpha :X\to G$ be the map defined by $\alpha (k)=\dot {w}k$ . The last map becomes K-K-equivariant if we consider the right action of K on X by multiplication and define the left action by $k'\ast k=\dot {w}^{-1}k'\dot {w}k$ . Using this map $\alpha $ , we define the map $A:\mathrm {pt}\cong K/K\to G/K$ by (3-9). Obviously, $A=A_w$ .

Let us choose any $w'\in W$ and set $B=A_{w'}$ . By (3-14),

$$ \begin{align*}\alpha B([k:1:{pt}])=\dot wk\dot w'K=\dot w\dot w'(\dot w'^{-1}k\dot w')K=\dot w\dot w'K=ww'K. \end{align*} $$

Hence, $\alpha B=A_{ww'}$ under the identification $K\mathop {\times }\limits _KK\mathop {\times }\limits _K\mathrm {pt}\cong \mathrm {pt}$ .

As P, Q, L are connected, $X/R$ , $P/Q$ , Y are singletons, and $H_K^{\bullet }(\mathrm {pt},\Bbbk )$ is the polynomial ring in finitely many variables of the second degree, Conditions (I)–(VIII) are satisfied. By Theorem 4.14, the homeomorphism $\theta $ is an isomorphism and it reads as the classical ${\mathcal R}$ - ${\mathcal R}$ -bimodule isomorphism

$$ \begin{align*} {\mathcal R}_w\otimes_{{\mathcal R}}{\mathcal R}_{w'}\cong{\mathcal R}_{ww'}. \end{align*} $$

5 Bott–Samelson varieties

5.1 Computation of the equivariant cohomology

Let G be a semisimple compact Lie group. We use Abbreviation (4-4). Additionally, we assume that $2$ is invertible in $\Bbbk $ . For any reflection t, we have two rings

$$ \begin{align*} {\mathcal R}(t)=H^{\bullet}_{G_t}(\mathrm{pt},\Bbbk),\quad {\mathcal R}^t=\{r\in{\mathcal R}\mathbin{\rm |} t(r)=r\}, \end{align*} $$

where $G_t$ is the group defined in the last paragraph of Section 2.14.

Lemma 5.1. For any reflection t, the quotient map $\pi _t:K\mathop {\backslash } E\to G_t\mathop {\backslash } E$ induces the isomorphism $\pi _t^*:{\mathcal R}(t)\stackrel \sim \to {\mathcal R}^t$ .

Proof. The result follows from the proof of [Br, Proposition 1] applied to the group $G_t$ , as its Weyl group consists of $2$ elements and $2$ is invertible in $\Bbbk $ .

For a sequence of reflections $\underline {t}=(t_1,\ldots ,t_n)$ , we define the following space:

$$ \begin{align*} \mathrm{BS}(\underline{t})=G_{t_1}\mathop{\times}\limits_K{G_{t_2}}\mathop{\times}\limits_K\cdots\mathop{\times}\limits_KG_{t_n}/K \end{align*} $$

called the Bott–Samelson variety for sequence $\underline {t}$ . The sequence $\underline {t}$ can be empty, in which case $\mathrm {BS}(\underline {t})$ is just the singleton. In what follows, we use the natural identification $\mathrm {pt}\,{}_K\!\times E\cong K\mathop {\backslash } E$ given by $K(pt,e)=Ke$ .

The torus K acts on the left on $\mathrm {BS}(\underline {t})$ (via the first factor for nonempty $\underline {t}$ ). Therefore, we can consider the equivariant cohomology denoted as follows:

$$ \begin{align*} H(\underline{t})=H_K^{\bullet}(\mathrm{BS}(\underline{t}),\Bbbk). \end{align*} $$

It is a left ${\mathcal R}$ -module with respect to the canonical action. However, there is the K-equivariant map

(5-1) $$ \begin{align} A_{\underline{t}}:\mathrm{BS}(\underline{t})\to G/K \end{align} $$

given by . Therefore, $H(\underline {t})$ is also a right ${\mathcal R}$ -module with the action twisted by $A_{\underline {t}}$ according to Section 3.1.

We represent $H(\underline {t})$ graphically by

If we need to indicate the elements of $\underline {t}$ directly, then we use the following notation:

$$ \begin{align*} \mathrm{BS}(t_1,\ldots,t_n)=\mathrm{BS}(\underline{t}),\quad H(t_1,\ldots,t_n)=H(\underline{t}). \end{align*} $$

We consider the following map $\varphi _{\underline {t}}:\mathrm {BS}(\underline {t})\,{}_K\!\times E\to (K\mathop {\backslash } E)^{n+1}$ :

This map can be constructed inductively with the help of the embedding $\varphi $ constructed in Section 3.4 as follows. If $\underline {t}=\underline {\varnothing }$ , then $\varphi _{\underline {t}}$ is the identity map.

Now suppose that $\underline {t}$ is not empty. Then we consider the following commutative diagram:

(5-2)

Here $\underline {t}'=(t_1,\ldots ,t_{n-1})$ is the truncated sequence (Section 2.2) and the map $\varphi $ is the map defined in Section 3.4 for the following set of data:

$$ \begin{align*} X=G_{t_1}\mathop{\times}\limits_K{G_{t_2}}\mathop{\times}\limits_K\cdots\mathop{\times}\limits_KG_{t_{n-1}},\quad Y=\mathrm{pt},\quad P=G_{t_n},\quad L=R=Q=K \end{align*} $$

and $\alpha :X\to G$ given by $[g_1:\cdots :g_{n-1}]\mapsto g_1\cdots g_{n-1}$ .

Lemma 5.2. The map $\varphi _{\underline {t}}$ is a topological embedding.

Proof. The result follows inductively from Diagram (5-2) and Theorem 3.9.

Using this embedding, we can define the map $\Theta _{\underline {t}}$ as the following composition:

where the first map is the cross product (Section 3.7). We consider the following commutative diagram:

(5-3)

where $\Theta $ is Map (3-18) corresponding to $\varphi $ . If we additionally set $M=K$ and define $B:Y\to G/M$ by $B(pt)=1M$ , then we get by Corollary 3.14 that $\Theta $ is a homomorphism of rings and ${\mathcal R}$ - ${\mathcal R}$ -modules. Note that (5-3) is commutative as (5-2) is so. Indeed,

$$ \begin{align*} \varphi^*(\mathop{\rm pr}\nolimits_1^*\varphi_{\underline{t}'}^*(\mathop{\rm pr}\nolimits_1^*(a_1)\cup\cdots\cup\mathop{\rm pr}\nolimits_{n+1}^*(a_1))\cup\mathop{\rm pr}\nolimits_2^*(a_{n+1})), \end{align*} $$

Hence, we need to prove that

$$ \begin{align*} \mathop{\rm pr}\nolimits_i\varphi_{\underline{t}'}\mathop{\rm pr}\nolimits_1\varphi=\mathop{\rm pr}\nolimits_i\varphi_{\underline{t}}\text{ for }1\leqslant i\leqslant n,\quad \mathop{\rm pr}\nolimits_2\varphi=\mathop{\rm pr}\nolimits_{n+1}\varphi_{\underline{t}}. \end{align*} $$

Both equalities follow if we append $\mathop{\rm pr}\nolimits _i$ to the left at both sides of the commutativity condition $(\varphi _{\underline {t}'}\times \mathrm {id})\varphi =\varphi _{\underline {t}}$ of (5-2). As $\Theta _{\underline {\varnothing }}=\mathrm {id}$ , we can use Diagram (5-3) to compute $\Theta _{\underline {t}}$ inductively. This computation and Corollary 3.14 prove that $\Theta _{\underline {t}}$ is a homomorphism of rings and ${\mathcal R}$ - ${\mathcal R}$ -bimodules.

Let us consider now the tensor product:

$$ \begin{align*} {\mathcal R}^{\otimes \underline{t}}={\mathcal R}\otimes_{{\mathcal R}(t_1)}\cdots\otimes_{{\mathcal R}(t_n)}{\mathcal R}, \end{align*} $$

where each ${\mathcal R}(t_i)$ acts on the left and on the right on ${\mathcal R}$ through $\pi _{t_i}$ , that is, $bm\hspace{-1pt}=\hspace{-1pt}\pi _{t_i}^*(b)\hspace{-1pt}\cup\hspace{-1pt} m$ and $mb=m\cup \pi _{t_i}^*(b)$ for any $m\in {\mathcal R}$ and $b\in {\mathcal R}(t_i)$ . In view of Lemma 5.1,

$$ \begin{align*} {\mathcal R}^{\otimes \underline{t}}={\mathcal R}\otimes_{{\mathcal R}^{t_1}}\cdots\otimes_{{\mathcal R}^{t_n}}{\mathcal R}. \end{align*} $$

We use the first equality when we apply the (iso)morphisms $\theta $ introduced in Section 3.7 and the second equality to perform algebraic computations.

Theorem 5.3. The map $\Theta _{\underline {t}}$ factors through the natural projection ${\mathcal R}^{\,{\otimes }_{\Bbbk }\, n+1}\to {\mathcal R}^{\otimes \underline {t}}$ to an isomorphism of rings and ${\mathcal R}$ - ${\mathcal R}$ -bimodules $\theta _{\underline {t}}:{\mathcal R}^{\otimes \underline {t}}\stackrel \sim \to H(\underline {t})$ .

Proof. Let us apply induction on the length of $\underline {t}$ . There is nothing to prove if $\underline {t}=\underline {\varnothing }$ , as $\Theta _{\underline {\varnothing }}=\mathrm {id}$ . Now suppose that $\underline {t}$ is not empty. We consider the following diagram:

where $\theta $ is the map corresponding to $\Theta $ from (5-3), as described in Section 3.7, and the dashed arrow is defined so that the trapezoid containing it is commutative. We need to prove that the triangle containing this arrow is also commutative. This is however so, as all other triangles, both trapezoids as well as the outer perimeter are commutative. The last claim follows from the commutativity of (5-3) and the inductive definition of $\theta _{\underline {t}'}$ . Note that $\theta $ is an isomorphism by Theorem 4.14, the validity of Condition (VIII) being guaranteed inductively by Lemma 2.3. Thus, $\theta _{\underline {t}}$ is a composition of isomorphisms and therefore is an isomorphism itself.

5.2 Concatenation

Our next aim is to prove that the isomorphisms $\theta _{\underline {t}}$ of Theorem 5.3 behave well under the concatenation of sequences. Let $\underline {t}=(t_1,\ldots ,t_n)$ and $\underline {r}=(r_1,\ldots ,r_m)$ be sequences of reflections. As in Section 3.4, we consider the embedding

$$ \begin{align*} \varphi_{\underline{t},\underline{r}}:\mathrm{BS}(\underline{tr})\,{}_K\!\times E\to(\mathrm{BS}(\underline{t})\,{}_K\!\times E)\times(\mathrm{BS}(\underline{r})\,{}_K\!\times E) \end{align*} $$

for the following set of data:

$$ \begin{align*} X=G_{t_1}\mathop{\times}\limits_K{G_{t_2}}\mathop{\times}\limits_K\cdots\mathop{\times}\limits_KG_{t_n},\quad Y=\mathrm{BS}(\underline{r}),\quad L=R=P=Q=K, \end{align*} $$

and $\alpha :X\to G$ defined by $[g_1:\cdots :g_n]\mapsto g_1\cdots g_n$ . Here we use the representation

$$ \begin{align*} \mathrm{BS}(\underline{tr})=X\mathop{\times}\limits_KK\mathop{\times}\limits_KY, \end{align*} $$

thus assuming

(5-4)

Setting additionally $M=K$ and defining $B:Y\to G/M$ by , we get by Theorem 4.14 the following isomorphisms of rings and ${\mathcal R}$ - ${\mathcal R}$ -bimodules:

where $\theta _{\underline {t},\underline {r}}$ is induced by $\varphi _{\underline {t},\underline {r}}$ as in Section 3.7.

Theorem 5.4. There is the following commutative diagram:

where the isomorphism of the bottom arrow is given by

$$ \begin{align*} (a_1\otimes\cdots\otimes a_{n+1})\otimes(b_1\otimes\cdots\otimes b_{m+1})\mapsto a_1\otimes\cdots\otimes a_n \otimes (a_{n+1}\cup b_1)\otimes b_2\otimes\cdots\otimes b_{m+1}. \end{align*} $$

Proof. Following the upper path,

$$ \begin{align*}\hspace{33pt} \varphi_{\underline{t},\underline{r}}^*(\mathop{\rm pr}\nolimits_1^*\varphi_{\underline{t}}^*(\mathop{\rm pr}\nolimits_1^*(a_1)\cup\cdots\cup\mathop{\rm pr}\nolimits_{n+1}^*(a_{n+1}))\cup\mathop{\rm pr}\nolimits_2^*\varphi_{\underline{r}}^*(\mathop{\rm pr}\nolimits_1^*(b_1)\cup\cdots\cup\mathop{\rm pr}\nolimits_{m+1}^*(b_{m+1}))). \end{align*} $$

Following the lower path,

Comparing the right-hand sides, we see that we need to prove the formulas

$$ \begin{align*} \mathop{\rm pr}\nolimits_i\varphi_{\underline{t}}\mathop{\rm pr}\nolimits_1\varphi_{\underline{t},\underline{r}}=\mathop{\rm pr}\nolimits_i\varphi_{\underline{tr}}\text{ for }1\leqslant i\leqslant n+1,\quad \mathop{\rm pr}\nolimits_j\varphi_{\underline{r}}\mathop{\rm pr}\nolimits_2\varphi_{\underline{t},\underline{r}}=\mathop{\rm pr}\nolimits_{j+n}\varphi_{\underline{tr}}\text{ for }1\leqslant j\leqslant m+1, \end{align*} $$

which follow from elementary calculations.

The maps $\varphi _{\underline {t},\underline {r}}$ were introduced for the universal principal bundle E. In what follows, we also use their compact versions $\varphi _{\underline {t},\underline {r}}^N$ (Remark 2.8).

5.3 Bott towers

We remember the main constructions of [GK]. Let n be a nonnegative integer and $\underline {c}=\{c_{i,j}\}_{1\leqslant i<j\leqslant n}$ be a collection of integers. The Bott tower [GK, Section 2.2] corresponding to $\underline {c}$ is the quotient

$$ \begin{align*} \mathrm{BT}(\underline{c})=({\mathbb C}^2-\{(0,0)\})^n/({\mathbb C}^\times)^n \end{align*} $$

with respect to the following action of $({\mathbb C}^\times )^n$ :

(5-5) $$ \begin{align} &(z_1,w_1,\ldots,z_n,w_n)(1,\ldots,1,a_i,1,\ldots,1)\nonumber\\ &\quad=(z_1,w_1,\ldots,z_{i-1},w_{i-1}, z_i a_i, w_i a_i,\ldots,z_j,w_j a_i^{c_{i,j}},\ldots), \end{align} $$

where $a_i$ is at the ith place. Note that $\mathrm {BT}(\underline {c})$ is a smooth complex manifold and thus is canonically oriented. We denote the orbit containing the sequence $(z_1,w_1,\ldots ,z_n,w_n)$ by $[z_1,w_1,\ldots ,z_n,w_n]$ . This notation agrees with the notation of points of Bott towers in [GK] and with our notation of points of $P^1(\mathbb C)$ introduced in Section 2.4. In the following lemma, we denote by $\langle \alpha _t,\alpha _r\rangle $ the integer such that $t(\alpha _r)=\alpha _r-\langle \alpha _r,\alpha _t\rangle \alpha _t$ .

Lemma 5.5. Let $\underline {t}=(t_1,\ldots ,t_n)$ be a sequence of reflections. Let us define $c_{i,j}=\langle \alpha _{t_j},\alpha _{t_i}\rangle $ and $\underline {c}=\{c_{i,j}\}_{1\leqslant i<j\leqslant n}$ . Then the manifolds $\mathrm {BT}(\underline {c})$ and $\mathrm {BS}(\underline {t})$ are homeomorphic.

Proof. Let us consider the three-dimensional sphere $S^3\hspace{-1pt}=\hspace{-1pt}\{(z,w)\hspace{-1pt}\in\hspace{-1pt} {\mathbb C}^2\mathbin{\rm |} |z|^2\hspace{-1pt}+\hspace{-1pt}|w|^2\hspace{-1pt}=\hspace{-1pt}1\}$ . We can construct the quotient $(S^3)^n/(S^1)^n$ with respect to the group action given by (5-5). Using the same notation for the orbits of this space as for the orbits of $\mathrm {BT}(\underline {c})$ , we define the homeomorphism $(S^3)^n/(S^1)^n\stackrel \sim \to \mathrm {BS}(\underline {t})$ as follows:

$$ \begin{align*} [z_1,w_1,\ldots,z_n,w_n]\mapsto\left.\left[\varphi_{\alpha_{t_1}}\!\!\left(\!\!\begin{array}{cc}z_1& -\bar w_1\\w_1&\bar z_1\end{array}\!\!\right):\cdots:\varphi_{\alpha_{t_n}}\!\!\left(\!\!\begin{array}{cc}z_n& -\bar w_n\\w_n&\bar z_n\end{array}\!\!\right)\right]\!\!\right]. \end{align*} $$

Here $\varphi _{\alpha _{t_i}}$ are the root homomorphisms as in Section 2.14. As the natural embedding $(S^3)^n\hookrightarrow ({\mathbb C}^2-\{(0,0)\})^n$ induces the homeomorphism $(S^3)^n/(S^1)^n\stackrel \sim \to \mathrm {BT}(\underline {c})$ , refer to [GK, Section 2.2], the required result follows.

The homomorphism described above defines two things: an orientation on $\mathrm {BS}(\underline {t})$ and a left K-action on $\mathrm {BT}(\underline {c})$ . This action is given by

$$ \begin{align*} k[z_1,w_1,\ldots,z_n,w_n]=[z_1,\alpha_{t_1}(k)^{-1}w_1,\ldots,z_n,\alpha_{t_n}(k)^{-1}w_n]. \end{align*} $$

Note that the coefficients $c_{i,j}$ are given by the same formula in [GK, Section 3.7] in the case where all reflections are simple.

In the special case of a sequence of length 1, we have $\mathrm {BS}(t)\cong \mathrm {BT}(\underline {\varnothing })=P^1(\mathbb C)$ . This isomorphism proves that

(5-6) $$ \begin{align} {}^{K\!}\mathrm{BS}(t)=\{1K,\dot tK\}, \end{align} $$

where $\dot t$ is a lifting of t (Section 2.14). We assume here and in the following that $\dot t$ is chosen within $G_t$ for any reflection t. Moreover, we assume that the neutral element of W is lifted to the neutral element of G. By Lemma 5.5,

Thus, in accordance with the identification of Section 2.14, we compute the equivariant Euler class (that is, the first Chern class), following the guidelines of [AF, Ch. 2, Section 3], as follows:

(5-7)

for N big enough.

5.4 Fixed points

Let $\underline {t}=(t_1,\ldots ,t_n)$ be a sequence of reflections. We denote by $\Gamma _{\underline {t}}$ the set of generalized combinatorial galleries whose elements are sequences $\underline {\gamma }=(\gamma _1,\ldots ,\gamma _n)$ , where $\gamma _i=t_i$ or $\gamma _i=1$ for each i.

Lemma 5.6. The set ${}^{K\!}\mathrm {BS}(\underline {t})$ consists of the points , where $n=|\underline {t}|$ and $\underline {\gamma }\in \Gamma _{\underline {t}}$ .

Proof. As K is normalized by W, the points are fixed by K. To prove the converse claim, let us apply induction on n. The case $n=0$ is obvious. Suppose that $n>0$ . Then $t_n$ is the last element of $\underline {t}$ . We consider the truncated sequence $\underline {t}'$ and two K-equivariant maps $\mathop{\rm tr}\nolimits :\mathrm {BS}(\underline {t})\to \mathrm {BS}(\underline {t}')$ and $\zeta :\mathrm {BS}(\underline {t})\to G/K$ given by

respectively. Let $a\in \!{}^{K\!}\mathrm {BS}(\underline {t})$ . Then $\mathop{\rm tr}\nolimits (a)\in \!{}^{K\!}\mathrm {BS}(\underline {t}')$ . By induction, we have a representation for some $(\gamma _1,\ldots \gamma _{n-1})\in \Gamma _{\underline {t}'}$ and $x_n\in G_{t_n}$ . However, $\zeta (a)\in \!{}^{K\!}(G/K)$ . Thus,

$$ \begin{align*} k\dot\gamma_1\cdots\dot\gamma_{n-1}x_nK=\dot\gamma_1\cdots\dot\gamma_{n-1}x_nK \end{align*} $$

for any $k\in K$ . Hence, $k'x_nK=x_nK$ , where $k'=(\dot \gamma _1\cdots \dot \gamma _{n-1})^{-1}k\dot \gamma _1\cdots \dot \gamma _{n-1}$ . As $k'$ is an arbitrary element of K, we get by (5-6) that $x_nK\in \!{}^{K\!}\mathrm {BS}(t_n)=\{1K,\dot t_nK\}$ . The result follows.

We identify $\underline {\gamma }$ with the point of $\mathrm {BS}(\underline {t})$ . For each $x\in W$ , we denote by $\Gamma _{\underline {t},x}$ the subset of $\Gamma _{\underline {t}}$ consisting of sequences $\underline {\gamma }$ such that $\gamma _1\cdots \gamma _n=x$ . According to Lemma 3.5, the embedding $i_{\underline {\gamma }}:\mathrm {pt}\hookrightarrow \mathrm {BS}(\underline {t})$ taking value $\underline {\gamma }\in \Gamma _{\underline {t},x}$ induces the homomorphism of ${\mathcal R}$ - ${\mathcal R}$ -bimodules

$$ \begin{align*} i_{\underline{\gamma}}^{\star}:H(\underline{t})\to{\mathcal R}_x. \end{align*} $$

Note that in this formula, the left actions are canonical, and the right actions on the domain and codomain are twisted by $A_{\underline {t}}$ and $A_{\underline {t}}i_{\underline {\gamma }}$ , respectively (Lemma 3.5). The last map takes only the value $xK$ . We can compute $i_{\underline {\gamma }}^{\star }$ in coordinates.

Theorem 5.7. For each $\underline {\gamma }\in \Gamma _{\underline {t},x}$ , the composition

is given by $ a_1\otimes \cdots \otimes a_{n+1}\mapsto a_1\cup \gamma _1(a_2)\cup \cdots \cup \gamma _1\cdots \gamma _n(a_{n+1}) $ .

Proof. Replacing $\theta _{\underline {t}}$ by $\Theta _{\underline {t}}$ , it remains to compute the following composition:

Following these maps,

(5-8)

It is easy to note that $\mathop{\rm pr}\nolimits _j\varphi _{\underline {t}}(i_{\underline {\gamma }}\times \mathrm {id})=K\mathop {\backslash }\rho _{(\gamma _1\cdots \gamma _{j-1})^{-1}}$ , where the last map is defined in Section 2.14. Therefore, by (2-8),

$$ \begin{align*} (\mathop{\rm pr}\nolimits_i\varphi_{\underline{t}}(i_{\underline{\gamma}}\times\mathrm{id}))^*(a_i)=(K\mathop{\backslash}\rho_{(\gamma_1\cdots\gamma_{i-1})^{-1}})^*(a_i) =\gamma_1\cdots\gamma_{i-1}(a_i). \end{align*} $$

The result follows from this formula and (5-8).

Using the Mayer–Vietoris isomorphism, we obtain that the restriction to ${}^{K\!}\mathrm {BS}(\underline {t})$ is the following homomorphism of ${\mathcal R}$ - ${\mathcal R}$ -bimodules:

$$ \begin{align*} H^{\bullet}_K(\mathrm{BS}(\underline{t}),\Bbbk)\to H^{\bullet}_K({}^K\mathrm{BS}(\underline{t}),\Bbbk)\stackrel\sim\to\bigoplus_{x\in W}\bigoplus_{\gamma\in\Gamma_{\underline{t},x}}{\mathcal R}_x. \end{align*} $$

We do not claim that this homomorphism is a monomorphism. However, this is true under some restrictions on $\Bbbk $ (for example, if $\Bbbk $ has no zero divisors, refer to [S1, Corollary 2.5]), in which case we say that the localization theorem holds.

6 Morphisms

6.1 The setup

In the notation of the rest of the paper, we replace any sequence $\underline {t}$ of length 1 by its unique element t. For example, $\varphi _{\underline {r},t}=\varphi _{\underline {r},\underline {t}}$ , $\theta _t=\theta _{\underline {t}}$ , $\theta _{\underline {r},t}=\theta _{\underline {r},\underline {t}}$ , ${\mathcal R}^{\otimes t}={\mathcal R}^{\otimes \underline {t}}$ , and so forth. We also no longer write the symbol of the cup product between elements of ${\mathcal R}$ .

We draw morphisms between bimodules $H(\underline {t})$ as usual from bottom to top. The easiest case is represented by trivial morphisms, which are drawn as vertical lines in the colors corresponding to the colors of the reflections:

Recall that for any reflection, we denote by $\alpha _t$ the positive root such that $t=\omega _{\alpha _t}$ (Section 2.14) and set

$$ \begin{align*} P_t(f)=\frac{f+t(f)}2,\quad \partial_t(f)=\frac{f-t(f)}{\alpha_t}. \end{align*} $$

The operator $\partial _t$ in the last formula is called the Demazure operator. We get $P_t(f)\in {\mathcal R}^t$ , $\partial _t(f)\in {\mathcal R}^t$ , and

(6-1) $$ \begin{align} f=P_t(f)+\partial_t(f)\,\frac{\alpha_t}2. \end{align} $$

An element m of an ${\mathcal R}$ - ${\mathcal R}$ -bimodule M is called central if $rm=mr$ for every $r\in {\mathcal R}$ . For example, if we consider ${\mathcal R}$ itself as ${\mathcal R}$ - ${\mathcal R}$ -bimodule, then all elements of ${\mathcal R}$ are central. However, for any reflection t, only the zero element of the standard bimodule ${\mathcal R}_t$ (Section 4.7) is central. Indeed, $m\in {\mathcal R}_t$ is central if and only if $rm=t(r)m$ for every $r\in {\mathcal R}$ . Substituting $r=\alpha _t$ , we get $2\alpha _tm=0$ . As $2$ is invertible, we get $m=0$ . Obviously, central elements are mapped to central ones by bimodule homomorphisms.

We use the shift of grading (Section 2.3) so that all homomorphisms of bimodules we consider are grading preserving. For example, we get the following exact sequence [EW, (3.4)]:

(6-2)

where $\lambda _t(r)=r({\alpha _t}/2)\otimes 1+r\otimes ({\alpha _t}/2)$ and $\sigma _t(f\otimes g)=ft(g)$ . Therefore, any central element of ${\mathcal R}\otimes _{{\mathcal R}^t}{\mathcal R}$ is in the kernel of $\sigma _t$ and thus in the image of $\lambda _t$ . Note that in [EW], t is supposed to be simple, but the above sequence is actually exact for any reflection t.

6.2 One-color morphisms

Let us fix a reflection t. Consider the natural embedding $\iota _t:\mathrm {pt}\to \mathrm {BS}(t)$ , which maps pt to . We get $\iota _t=i_{(1)}$ in the notation of Section 5.4. We get the equivariant pull-back

$$ \begin{align*} \iota_t^{\star}:H(t)\to {\mathcal R}, \end{align*} $$

which we represent as the diagram

(ι _t ^⋆)

This map is a homomorphism of ${\mathcal R}$ - ${\mathcal R}$ -bimodules by Lemma 3.5. By Theorem 5.7, we get that the composition map

is given by

(6-3) $$ \begin{align} \iota_t^{\star}\theta_t(a\otimes b)=ab. \end{align} $$

Now we consider the negated equivariant push-forward

$$ \begin{align*} -\iota_{t\star}:{\mathcal R}\to H(t)(2). \end{align*} $$

Recall that a number in round brackets means the degree shift (Section 2.3). We represent the above morphism as follows:

(−ι _t⋆)

By Lemma 3.6, this map is a homomorphism of ${\mathcal R}$ - ${\mathcal R}$ -bimodules. We want to compute the composition

(6-4)

It suffices to compute the image of $1$ . As the element $-\theta _t^{-1}i_{t\star }(1)$ is central and of degree $2$ , the short exact sequence (6-2) and the argument following it show that

$$ \begin{align*} -\theta_t^{-1}i_{s\star}(1)=c\alpha_t\otimes 1+c\otimes\alpha_t \end{align*} $$

for some $c\in \Bbbk $ . To compute this constant, first apply $-\theta _t$ and then $\iota _t^{\star }$ to the formula above. By (5-7), Theorem 5.7, and (6-3),

Hence, $c=1/2$ . As all maps in (6-4) are homomorphisms of bimodules,

$$ \begin{align*} \theta_t^{-1}(-i_{t\star})(d)=d\frac{\alpha_t}2\otimes 1+d\otimes\frac{\alpha_t}2. \end{align*} $$

Let $\mu _t:\mathrm {BS}(t,t)\to \mathrm {BS}(t)$ be the map given by . Taking the pull-back, we get the map

$$ \begin{align*} \mu_t^{\star}:H(t)\to H(t,t). \end{align*} $$

We draw this diagram as follows:

(μ _t⋆)

This map is a homomorphism of ${\mathcal R}$ - ${\mathcal R}$ -bimodules by Lemma 3.5. We are going to compute the composition

(6-5)

Computing in degree zero,

$$ \begin{align*} \mu_t^{\star}\theta_t(1\otimes 1)=1=\theta_{(t,t)}(1\otimes 1\otimes 1), \end{align*} $$

where the central unit is the constant unit function on $\mathrm {BS}(t,t){}_K\times E$ and all other units are the constant unit function on $K\mathop {\backslash } E$ . These functions are considered as cohomology classes and pull-back to constant unit functions, which explains the computation above.

As all maps in (6-5) are homomorphisms of bimodules,

$$ \begin{align*} \theta_{(t,t)}^{-1}\mu_t^{\star}\theta_t(a\otimes b)=a\otimes1\otimes b. \end{align*} $$

As expected, the merge diagram

(−μ _t⋆)

is defined to be the negated push-forward map $-\mu _{t\star }:H(t,t)\to H(t)(-2)$ . We postpone the computation of its coordinate form until we manage to extend diagram (−ι _t⋆ ) horizontally.

6.3 Horizontal extensions

We apply the concatenation properties proved in Section 5.2. First, let us consider the planar diagram

(ι _{ṟ, t} ^⋆)

for a reflection t and a sequence of reflections $\underline {r}=(r_1,\ldots ,r_n)$ (the black solid strings can be of any color). Let $\underline {r}t=(r_1,\ldots ,r_n,t)$ be the concatenated sequence and $\iota _{\underline {r},t}:\mathrm {BS}(\underline {r})\hookrightarrow \mathrm {BS}(\underline {r}t)$ be the embedding given by . We claim that the diagram

(6-6)

is commutative. Indeed, for any $a\in H(\underline {r})$ and $b\in H(t)$ ,

$$ \begin{align*} \theta_{\underline{r},\underline{\varnothing}}(\mathrm{id}\otimes\iota_t^{\star})(a\otimes b)=\theta_{\underline{r},\underline{\varnothing}}(a\otimes\iota_t^{\star}(b)) =\varphi_{\underline{r},\underline{\varnothing}}^*(\mathop{\rm pr}\nolimits_1^*(a)\cup\mathop{\rm pr}\nolimits_2^*\iota_t^{\star}(b)), \end{align*} $$

$$ \begin{align*} \iota_{\underline{r},t}^{\star}\theta_{\underline{r},t}(a\otimes b)=\iota_{\underline{r},t}^{\star}\varphi_{\underline{r},t}^*(\mathop{\rm pr}\nolimits_1^*(a)\cup\mathop{\rm pr}\nolimits_2^*(b)). \end{align*} $$

Comparing the results, we see that it suffices to prove the equalities

(6-7) $$ \begin{align} \mathop{\rm pr}\nolimits_1\varphi_{\underline{r},\underline{\varnothing}}=\mathop{\rm pr}\nolimits_1\varphi_{\underline{r},t}(\iota_{\underline{r},t}\, {\mathop{{}_{K}\times}}\, \mathrm{id}),\quad(\iota_t\, {\mathop{{}_{K}\times}}\, \mathrm{id})\mathop{\rm pr}\nolimits_2\varphi_{\underline{r},\underline{\varnothing}}=\mathop{\rm pr}\nolimits_2\varphi_{\underline{r},t}(\iota_{\underline{r},t}\, {\mathop{{}_{K}\times}}\, \mathrm{id}). \end{align} $$

They follow directly from the identification rule in (5-4) for concatenation operators and the definition in (3-10).

Now let us extend ( ι ^⋆ _ṟ,t ) to the right

(ι _{ṟ, t, v} ^⋆)

for another sequence of reflections $\underline {v}=(v_1,\ldots ,v_m)$ . Let $\underline {r}t\underline {v}=(r_1,\ldots ,r_n,t,v_1,\ldots ,v_m)$ be the concatenated sequence and $\iota _{\underline {r},t,\underline {v}}:\mathrm {BS}(\underline {rv})\hookrightarrow \mathrm {BS}(\underline {r}t\underline {v})$ be the map defined by . We get the commutative diagram

(6-8)

Inserting (6-3) to (6-6) and (6-8), we get the formula in coordinates

$$ \begin{align*} &\theta_{\underline{rv}}^{-1}\iota_{\underline{r},t,\underline{v}}^{\star}\theta_{\underline{r}t\underline{v}}(a_1\otimes\cdots\otimes a_{n+1}\otimes b_1\otimes\cdots\otimes b_{m+1})\\&\quad=a_1\otimes\cdots\otimes a_n\otimes a_{n+1}b_1\otimes b_2\otimes\cdots\otimes b_{m+1}. \end{align*} $$

Let us extend (−ι _t⋆ ) horizontally. To this end, we first prove that the diagram

(6-9)

is commutative. It is more difficult, as it involves push-forward operators. For any $a\in H(\underline {r})$ and $b\in {\mathcal R}$ , we get by the first equality of (6-7) and the projection formula (Proposition 2.9),

(6-10) $$ \begin{align} \iota_{\underline{r},t\star}\theta_{\underline{r},\underline{\varnothing}}(a\otimes b)&=\iota_{\underline{r},t\star}\varphi_{\underline{r},\underline{\varnothing}}^*(\mathop{\rm pr}\nolimits_1^*(a)\cup\mathop{\rm pr}\nolimits_2^*(b)) =\iota_{\underline{r},t\star}((\mathop{\rm pr}\nolimits_1\varphi_{\underline{r},\underline{\varnothing}})^*(a)\cup (\mathop{\rm pr}\nolimits_2\varphi_{\underline{r},\underline{\varnothing}})^*(b))\nonumber\\ &=\iota_{\underline{r},t\star}(\iota_{\underline{r},t}^{\star}(\mathop{\rm pr}\nolimits_1\varphi_{\underline{r},t})^*(a)\cup (\mathop{\rm pr}\nolimits_2\varphi_{\underline{r},\underline{\varnothing}})^*(b))\nonumber\\ &=(\mathop{\rm pr}\nolimits_1\varphi_{\underline{r},t})^*(a)\cup\iota_{\underline{r},t\star}(\mathop{\rm pr}\nolimits_2\varphi_{\underline{r},\underline{\varnothing}})^*(b). \end{align} $$

Let us consider the compatibly oriented Cartesian square

By (2-4), we get $(\iota _{\underline {r},t}\,{\mathop{{}_{K}\times}}\, \mathrm {id})_*(\mathop{\rm pr}\nolimits _2\varphi _{\underline {r},\underline {\varnothing }}^N)^*=(\mathop{\rm pr}\nolimits _2\varphi _{\underline {r},t}^N)^*(\iota _t\,{\mathop{{}_{K}\times}}\, \mathrm {id})_*$ . Taking the limit $N\to \infty $ , we get $\iota _{\underline {r},t\star }(\mathop{\rm pr}\nolimits _2\varphi _{\underline {r},\underline {\varnothing }})^*=(\mathop{\rm pr}\nolimits _2\varphi _{\underline {r},t})^*\iota _{t\star }$ . Applying this substitution to the right-hand side of (6-10),

$$ \begin{align*} \iota_{\underline{r},t\star}\theta_{\underline{r},\underline{\varnothing}}(a\otimes b)&=(\mathop{\rm pr}\nolimits_1\varphi_{\underline{r},t})^*(a)\cup(\mathop{\rm pr}\nolimits_2\varphi_{\underline{r},t})^*\iota_{t\star}(b)\\ &=\varphi_{\underline{r},t}^*(\mathop{\rm pr}\nolimits_1^*(a)\cup\mathop{\rm pr}\nolimits_2^*\iota_{t\star}(b))=\theta_{\underline{r},t}(a\otimes \iota_{t\star}(b))=\theta_{\underline{r},t}(\mathrm{id}\otimes\iota_{t\star})(a\otimes b). \end{align*} $$

This equality proves the commutativity of (6-9). We prove similarly that the diagram

is commutative. Computing in coordinates,

(6-11) $$ \begin{align} &\theta_{\underline{r}t\underline{v}}^{-1}(-\iota_{\underline{r},t,\underline{v}\star})\theta_{\underline{rv}}(a_1\otimes\cdots\otimes a_n\otimes d\otimes b_2\otimes\cdots\otimes b_{m+1})\nonumber\\ &\quad=a_1\otimes\cdots\otimes a_n\otimes\bigg( d\frac{\alpha_t}2\otimes 1+d\otimes\frac{\alpha_t}2\bigg)\otimes b_2\otimes\cdots\otimes b_{m+1}. \end{align} $$

This morphism is represented by the diagram

(−ι _{ṟ,t,v_⋆})

The split map $\mu _t^{\star }$ can be extended horizontally in the same way. Consider the diagram

(μ _{ṟ, t, v_} ^⋆)

for sequences of reflections $\underline {r}=(r_1,\ldots ,r_n)$ and $\underline {v}=(v_1,\ldots ,v_m)$ . Let $\mu _{\underline {r},t,\underline {v}}:\mathrm {BS}(\underline {r}tt\underline {v})\to \mathrm {BS}(\underline {r}t\underline {v})$ be the map given by

where $\underline {r}tt\underline {v}=(r_1,\ldots ,r_n,t,t,v_1,\ldots ,v_m)$ . Arguing as for $\iota _{\underline {r},t,\underline {v}}^{\star }$ ,

$$ \begin{align*} \theta_{\underline{r}tt\underline{v}}^{-1}\mu_{\underline{r},t,\underline{v}}^{\star}\theta_{\underline{r}t\underline{v}}(a_1\otimes\cdots\otimes a_{n+1}\otimes b_1\otimes\cdots\otimes b_{m+1}) =a_1\otimes\cdots\otimes a_{n+1}\otimes1\otimes b_1\otimes\cdots\otimes b_{m+1}. \end{align*} $$

At this point, we can compute the coordinate form of the merge diagram (−μ _t⋆ ). We clearly have $\mu _t\iota _{t,t,\underline {\varnothing }}=\mathrm {id}$ . Taking the push-forwards, we get $(-\mu _{t\star })(-\iota _{t,t,\underline {\varnothing }\star })=\mathrm {id}$ . Expressed diagrammatically, we get our first relation:

Note that we have proved this relation without resorting to coordinatization. By (6-11),

$$ \begin{align*} 1\otimes1=\theta_t^{-1}\mu_{t\star}\iota_{t,t,\varnothing\star}\theta_t(1\otimes 1)&=\theta_t^{-1}(-\mu_{t\star})\theta_{(t,t)}\bigg(1\otimes\frac{\alpha_t}2\otimes 1+1\otimes 1\otimes\frac{\alpha_t}2\bigg)\\ &=\theta_t^{-1}(-\mu_{t\star})\theta_{(t,t)}\bigg(1\otimes\frac{\alpha_t}2\otimes 1\bigg)-\theta_t^{-1}\mu_{t\star}\theta_{(t,t)}(1\otimes 1\otimes 1)\frac{\alpha_t}2. \end{align*} $$

As $\theta _t^{-1}\mu _{t\star }\theta _{(t,t)}(1\otimes 1\otimes 1)=0$ for the degree reason,

$$ \begin{align*} \theta_t^{-1}(-\mu_{t\star})\theta_{(t,t)}\bigg(1\otimes\frac{\alpha_t}2\otimes 1\bigg)=1\otimes1. \end{align*} $$

Let us take any $b\in H(t)$ . Applying (6-1) and the above formula,

$$ \begin{align*} &\theta_t^{-1}(-\mu_{t\star})\theta_{(t,t)}(1\otimes b\otimes 1)\\ &\quad=-P_t(b)\,\theta_t^{-1}\mu_{t\star}\theta_{(t,t)}(1\otimes 1\otimes 1) +\partial_t(b)\,\theta_t^{-1}(-\mu_{t\star})\theta_{(t,t)}\bigg(1\otimes\frac{\alpha_t}2\otimes 1\bigg) =\partial_t(b)\otimes 1. \end{align*} $$

As this map is a homomorphism of bimodules,

$$ \begin{align*} \theta_t^{-1}(-\mu_{t\star})\theta_{(t,t)}(a\otimes b\otimes c)=a\partial_t(b)\otimes c. \end{align*} $$

The arguments described in this section allow us to extend $-\mu _{t\star }$ to the morphism $-\mu _{\underline {r},t,\underline {v}\star }$ represented by the diagram

(−μ _{ṟ, t, v_⋆})

and prove the coordinate formula

$$ \begin{align*} &\theta_{\underline{r}t\underline{v}}^{-1}(-\mu_{\underline{r},t,\underline{v}\star})\theta_{\underline{r}tt\underline{v}}(a_1\otimes\cdots\otimes a_n\otimes a\otimes b\otimes c\otimes b_2\otimes\cdots\otimes b_{m+1})\\ &\quad=a_1\otimes\cdots\otimes a_n\otimes a\partial_t(b)\otimes c\otimes b_2\otimes\cdots\otimes b_{m+1}. \end{align*} $$

6.4 Generalized Bott–Samelson varieties

For any nonempty set S of simple reflections, let $G_S$ be the subgroup of G generated by all groups $G_s$ , where $s\in S$ . Let $\underline {S}=(S_1,\ldots ,S_n)$ be a sequence of nonempty sets of simple reflections. Then we define

$$ \begin{align*} \mathrm{BS}(\underline{S})=G_{S_1}\mathop{\times}\limits_K{G_{S_2}}\mathop{\times}\limits_K\cdots\mathop{\times}\limits_KG_{S_n}/K. \end{align*} $$

Clearly, if each $S_i$ is a singleton, then $\mathrm {BS}(\underline {S})=\mathrm {BS}(\underline {s})$ , where $S_i=\{s_i\}$ and $\underline {s}=(s_1,\ldots ,s_n)$ . Bearing in mind this fact, we omit brackets for singletons. For example, we abbreviate $\mathrm {BS}(\{s\},\{s',\tilde s\},\{\mathring s\},\{\ddot s\})$ to $\mathrm {BS}(s,\{s',\tilde s\},{\mathring s},\ddot s)$ . We denote the equivariant cohomology by $H(\underline {S})=H_K^{\bullet }(\mathrm {BS}(\underline {S}),\Bbbk )$ , use the similar abbreviation, and draw $H(\underline {S})$ and the identical morphisms between them similarly to the cohomologies and morphisms for the usual Bott–Samelson varieties. For example, the identity map $H(s,\{s',\tilde s\},{\mathring s},\ddot s)\to H(s,\{s',\tilde s\},{\mathring s},\ddot s)$ is depicted as

The variety $\mathrm {BS}(\underline {S})$ has a complex structure coming from the following algebraic realization:

$$ \begin{align*} \mathrm{BS}(\underline{S})\cong P_{S_1}\mathop{\times}\limits_B{P_{S_2}}\mathop{\times}\limits_B\cdots\mathop{\times}\limits_BP_{S_n}/B, \end{align*} $$

where B and $P_{S_i}$ are the Borel subgroup and the minimal parabolic subgroup containing $S_i$ of the complexification $G^c$ of G, respectively. In this way, $\mathrm {BS}(\underline {S})$ receives a complex structure and thus an orientation. We also get $G/K\cong G^c/B$ and thus the quotient $G/K$ also receives a complex structure. Also note that $H_B^{\bullet }(\mathrm {pt},\Bbbk )\cong H_T^{\bullet }(\mathrm {pt},\Bbbk )\cong H_K^{\bullet }(\mathrm {pt},\Bbbk )$ , where T is the maximal complex torus in $G^c$ containing K.

In what follows, we consider only the case where each set $S_i$ is a singleton with at most one exception where this set consists of two distinct simple reflections (as in the example above).

6.5 Two-color morphisms

In the rest of the paper, we consider only sequences of simple reflections. For the simplicity of exposition, we omit the coordinatization maps $\theta _s$ , and thus think of them as identity maps. We denote

$$ \begin{align*} x_s=\frac{\alpha_s}2,\quad c_s=x_s\otimes 1+1\otimes x_s \end{align*} $$

for any simple reflection s.

If we consider $H(\underline {s})$ , where $\underline {s}=(s_1,\ldots ,s_n),$ as a left ${\mathcal R}$ -module, then it has the following ${\mathcal R}$ -basis:

$$ \begin{align*} \{1\otimes x_{s_1}^{\varepsilon_1}\otimes\cdots\otimes x_{s_n}^{\varepsilon_n}\mathbin{\rm |} \varepsilon_1,\ldots,\varepsilon_n\in\{0,1\}\}. \end{align*} $$

This ${\mathcal R}$ -basis consists of $2^n$ elements. We denote by $H(\underline {s})^{<}$ the left ${\mathcal R}$ -submodule of $H(\underline {s})$ generated by all above basis elements such that $\varepsilon _i=0$ for some i. The remaining basis element $1\otimes x_{s_1}\otimes \cdots \otimes x_{s_n}$ is called the normal element of $H(\underline {s})$ ; refer to [Li, Définition 4.6].

We leave the proof of the following result to the reader.

Proposition 6.1. $c_{s_1}\cdots c_{s_n}=1\otimes x_{s_1}\otimes \cdots \otimes x_{s_n}+h$ for some $h\in H(\underline {s})^{<}$ .

For any distinct simple reflections s and $\tilde s$ , we denote by $m_{s,\tilde s}$ the order of the product $s\tilde{s}$ . We have $m_{s,\tilde s}=m_{\tilde s,s}\in \{2,3,4,6\}$ . We define the following sequence:

$$ \begin{align*} [s,\tilde s]=\left\{\!\! \begin{array}{ll} (s,\tilde s)&\text{ if }m_{s,\tilde s}=2,\\ (s,\tilde s,s)&\text{ if }m_{s,\tilde s}=3,\\ (s,\tilde s,s,\tilde s)&\text{ if }m_{s,\tilde s}=4,\\ (s,\tilde s,s,\tilde s,s,\tilde s)&\text{ if }m_{s,\tilde s}=6. \end{array} \right. \end{align*} $$

The product of the reflections of $[s,\tilde s]$ is denoted by $w_{s,\tilde s}$ . The braid relation for this pair reads as $w_{s,\tilde s}=w_{\tilde s,s}$ . We use the notation $\mathrm {BS}(s,\tilde s,\ldots )=\mathrm {BS}([s,\tilde{s}])$ and $H(s,\tilde{s},\ldots )= H([s,\tilde s])$ , and denote by $1\otimes x_s\otimes x_{\tilde{s}}\otimes \cdots $ the normal element of $H(s,\tilde s,\ldots )$ . Similarly, $c_sc_{\tilde s}\cdots $ denotes one of the products $c_sc_{\tilde s}$ , $c_sc_{\tilde s}c_s$ , $c_sc_{\tilde s}c_sc_{\tilde s}$ , $c_sc_{\tilde s}c_sc_{\tilde s}c_sc_{\tilde s}$ , depending on $m_{s,\tilde s}$ .

The image of the twisting map $A_{[s,\tilde s]}$ , refer to (5-1), is actually contained in the Schubert variety $X_{s,\tilde s}=\overline {K_{w_{s,\tilde s}}/K}=\mathrm {BS}(\{s,\tilde s\})$ . Thus, $A_{[s,\tilde s]}$ can be regarded as the map $\eta _{s,\tilde s}:\mathrm {BS}(s,\tilde s,\ldots )\to X_{s,\tilde s}$ . The twisting maps for both sides are $A_{[s,\tilde s]}$ and the natural inclusion to $G/K$ , respectively. Note also that both these spaces are smooth manifolds having real dimension $2m_{s,\tilde s}$ . Therefore, we get the following two morphisms of ${\mathcal R}$ - ${\mathcal R}$ -bimodules:

$$ \begin{align*} \eta_{s,\tilde s}^{\star}:H_K^{\bullet}(X_{s,\tilde s},\Bbbk)\to H(s,\tilde s,\ldots),\quad \eta_{s,\tilde s\star}:H(s,\tilde s,\ldots)\to H_K^{\bullet}(X_{s,\tilde s},\Bbbk) \end{align*} $$

presented by the diagrams

Here the dash-dotted line can be either dotted or solid, depending on the parity of $m_{s,\tilde s}$ .

First, we calculate the following composition.

Lemma 6.2. $\eta _{s,\tilde s\star }\eta _{s,\tilde s}^{\star }=\mathrm {id}$ .

Proof. Applying the projection formula (Proposition 2.9),

$$ \begin{align*} \eta_{s,\tilde s\star}\eta_{s,\tilde s}^{\star}(h)=\eta_{s,\tilde s\star}(1\cup\eta_{s,\tilde s}^{\star}(h))=\eta_{s,\tilde s\star}(1)\cup h \end{align*} $$

for any $h\in H_K^{\bullet }(X_{s,\tilde s},\Bbbk )$ . Therefore, it suffices to prove that $\eta _{s,\tilde s\star }(1)=1$ . There is an open subset $V\subset X_{s,\tilde s}$ such that $\eta _{s,\tilde s}$ induces the orientation-preserving diffeomorphism $\eta ^{\prime }_{s,\tilde s}:U\stackrel \sim \to V$ , where $U=\eta _{s,\tilde s}^{-1}(V)$ . Consider the following Cartesian square:

By (the equivariant version of) (2-4),

$$ \begin{align*} j_V^{\star}\eta_{s,\tilde s\star}(1)=\eta^{\prime}_{s,\tilde s\star}j_U^{\star}(1)=\eta^{\prime}_{s,\tilde s\star}(1)=1. \end{align*} $$

As $X_{s,\tilde s}$ is connected, the above calculation proves that $\eta _{s,\tilde s\star }(1)=1$ .

Diagramatically expressed, this lemma looks as follows:

6.6 The $2m_{s,\tilde s}$ -valent vertex

Here, we are going to consider the composition $\eta _{\tilde s,s}^{\star }\eta _{s,\tilde s\star }:H(s,\tilde s,\ldots )\to H(\tilde s,s,\ldots )$ , which is a morphism of ${\mathcal R}$ - ${\mathcal R}$ -bimodules. It is depicted as follows:

Note that all such morphisms are proportional by [Li, Proposition 4.3]. In this paper, $2$ was assumed to be invertible in $\Bbbk $ .

Lemma 6.3. $\ker \mu _{s,\tilde s\star }\subset H(s,\tilde s,\ldots )^{<}$ .

Proof. Let $h\in \ker \mu _{s,\tilde s\star }$ . We have $h=\alpha \otimes x_s\otimes x_{\tilde s}\otimes \cdots +h'$ for some $h'\in H(s,\tilde s,\ldots )^{<}$ . For reasons of degree, we get $\eta _{\tilde s,s}^{\star }\eta _{s,\tilde s\star }(h')\in H(\tilde s,s,\ldots )^{<}$ . Therefore, it follows from $\eta _{\tilde s,s}^{\star }\eta _{s,\tilde s\star }(h)=0$ that

$$ \begin{align*} \alpha\,\eta_{\tilde s,s}^{\star}\eta_{s,\tilde s\star}(1\otimes x_s\otimes x_{\tilde s}\otimes\cdots)\in H(\tilde s,s,\ldots)^{<}. \end{align*} $$

By [Li, Proposition 4.3 and Lemme 4.7], this is only possible if $\alpha =0$ .

Our next aim is to prove the following normalization condition.

Lemma 6.4. $\eta _{\tilde s,s}^{\star }\eta _{s,\tilde s\star }(1\otimes x_s\otimes x_{\tilde s}\otimes \cdots )\hspace{-1.5pt}=\hspace{-1.5pt}1\otimes x_{\tilde s}\otimes x_s\otimes \cdots\hspace{-1pt} +\hspace{-1pt}h$ for some $h\hspace{-1pt}\in\hspace{-1pt} H (\tilde s,s,\ldots )^{<}$ .

Proof. Let us consider the following chain of inclusions:

where $s'=s$ or $s'=\tilde s$ depending on the parity of $m_{s,\tilde s}$ . We denote the resulting composition by $\iota $ . Its image is . Taking the equivariant push-forward

we get by (6-11) that the image of $(-1)^{m_{s,\tilde s}}$ is equal to $c_sc_{\tilde s}\cdots $ . Hence, $\eta _{s,\tilde s\star }(c_sc_{\tilde s}\cdots )=(\eta _{s,\tilde s}\iota )_\star ((-1)^{m_{s,\tilde s}})$ . Arguing similarly, we get $\eta _{\tilde s,s\star }(c_{\tilde s}c_s\cdots )=(\eta _{\tilde s,s}\iota )_\star ((-1)^{m_{s,\tilde s}})$ . As $\eta _{s,\tilde s}\iota =\eta _{\tilde s,s}\iota $ , we get by Lemmas 6.2 and 6.3 that

$$ \begin{align*} \eta_{\tilde s,s}^{\star}\eta_{s,\tilde s\star}(c_sc_{\tilde s}\cdots)-c_{\tilde s}c_s\cdots\in\ker\eta_{\tilde s,s\star}\subset H(\tilde s,s,\ldots)^{<}. \end{align*} $$

To conclude the proof, it suffices to apply Proposition 6.1 and the fact that $\eta _{\tilde s,s}^{\star }\eta _{s,\tilde s\star }$ , being a degree-preserving homomorphism $H(s,\tilde s,\ldots )\to H(\tilde s,s,\ldots )$ of left ${\mathcal R}$ -modules, maps $H(s,\tilde s,\ldots )^{<}$ to $H(\tilde s,s,\ldots )^{<}$ .

We have just proved that the composition $\eta _{\tilde s,s}^{\star }\eta _{s,\tilde s\star }$ is just the map $f_{s,\tilde s}$ from [Li, Lemme 4.7].

6.7 The Jones–Wenzl projector

This map is given by the composition $\eta _{s,\tilde s}^{\star }\eta _{s,\tilde s\star }$ and is represented by the diagram:

(η _{s~, s} ^⋆ η _{s, s~⋆})

From Lemma 6.2, we immediately get the relations:

6.8 Two-color dot contraction

As an example for $m_{s,\tilde s}=3$ , let us prove the following relation:

Indeed, the left-hand side and the right-hand side are equal to

$$ \begin{align*} \iota_{(\tilde s,s),\tilde s,\underline{\varnothing}}^{\star}\eta_{\tilde s,s}^{\star}\eta_{s,\tilde s\star}=(\eta_{\tilde s,s}\iota_{(\tilde s,s),\tilde s,\underline{\varnothing}})^{\star}\eta_{s,\tilde s\star},\quad \iota_{\underline{\varnothing},s,(\tilde s,s)}^{\star}\eta_{s,\tilde s}^{\star}\eta_{s,\tilde s\star}=(\eta_{s,\tilde s}\iota_{\underline{\varnothing},s,(\tilde s,s)})^{\star}\eta_{s,\tilde s\star}, \end{align*} $$

respectively. Hence, it suffices to prove that $\eta _{\tilde s,s}\iota _{(\tilde s,s),\tilde s,\underline {\varnothing }}=\eta _{s,\tilde s}\iota _{\underline {\varnothing },s,(\tilde s,s)}$ , which is obvious.

6.9 Horizontal extensions of two-color morphisms

Finally, it remains to extend the morphisms $\eta _{s,\tilde s}^{\star }$ and $\eta _{s,\tilde s\star }$ horizontally. It can be done similarly to the method used in Section 6.3. First, let $\underline {\mathring {s}}=(\mathring {s}_1,\ldots ,\mathring {s}_n)$ be a sequence of simple reflections. Then we define the map

$$ \begin{align*} \eta_{\underline{\mathring{s}},s,\tilde s}:\mathrm{BS}(\mathring{s}_1,\ldots,\mathring{s}_n,s,\tilde s,\ldots)\to\mathrm{BS}(\mathring{s}_1,\ldots,\mathring{s}_n,\{s,\tilde s\}) \end{align*} $$

by . We have the following commutative diagram:

where $\theta _{\underline {\mathring {s}},s,\tilde s}$ corresponds to

$$ \begin{align*} \varphi_{\underline{\mathring{s}},s,\tilde s}:\mathrm{BS}(\mathring{s}_1,\ldots,\mathring{s}_n,\{s,\tilde s\})\,{}_K\!\times E\to(\mathrm{BS}(\underline{\mathring{s}})\,{}_K\!\times E)\times(X_{s,\tilde s}\,{}_K\!\times E) \end{align*} $$

as in Section 3.4 for the following set of data:

$$ \begin{align*} X=G_{\mathring s_1}\mathop{\times}\limits_K{G_{\mathring s_2}}\mathop{\times}\limits_K\cdots\mathop{\times}\limits_KG_{\mathring s_n},\quad Y=X_{s,\tilde s},\quad L=R=P=Q=K, \end{align*} $$

and $\alpha :X\to G$ defined by $[g_1:\cdots :g_n]\mapsto g_1\cdots g_n$ .

Now let $\underline {\ddot s}=(\ddot s_1,\ldots ,\ddot s_m)$ be another sequence of simple reflections. We define the map

$$ \begin{align*} \eta_{\underline{\mathring s},s,\tilde s,\underline{\ddot s}}:\mathrm{BS}(\mathring s_1,\ldots,\mathring s_n,s,\tilde s,\ldots,\ddot s_1,\ldots,\ddot s_m)\to\mathrm{BS}(\mathring s_1,\ldots,\mathring s_n,\{s,\tilde s\},\ddot s_1,\ldots,\ddot s_m) \end{align*} $$

by

We have the following commutative diagram:

where $\theta _{\underline {\mathring s},s,\tilde s,\underline {\ddot s}}$ is defined similarly to $\theta _{\underline {\mathring s},s,\tilde s}$ . We leave it to the reader to write down similar diagrams for push-forwards, to draw the corresponding diagrams and to compose them (refer to the examples of diagrams in Section 1).