Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T21:20:15.257Z Has data issue: false hasContentIssue false
  • English
  • Français

UNEXPECTED AVERAGE VALUES OF GENERALIZED VON MANGOLDT FUNCTIONS IN RESIDUE CLASSES

Part of: Zeta and $L$-functions: analytic theory Multiplicative number theory

Published online by Cambridge University Press:  17 July 2020

NICOLAS ROBLES  and
ARINDAM ROY Open the ORCID record for ARINDAM ROY [Opens in a new window]
NICOLAS ROBLES
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, 1409 West Green Street, Urbana, IL61801, USA e-mail: nirobles@illinois.edu
ARINDAM ROY*
Affiliation:
Department of Mathematics and Statistics, UNC Charlotte, 9201 University City Blvd., Charlotte, NC28223, USA
*
e-mail: aroy15@uncc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In order to study integers with few prime factors, the average of 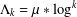$\unicode[STIX]{x1D6EC}_{k}=\unicode[STIX]{x1D707}\ast \log ^{k}$ has been a central object of research. One of the more important cases, 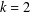$k=2$, was considered by Selberg [‘An elementary proof of the prime-number theorem’, Ann. of Math. (2)50 (1949), 305–313]. For 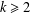$k\geq 2$, it was studied by Bombieri [‘The asymptotic sieve’, Rend. Accad. Naz. XL (5)1(2) (1975/76), 243–269; (1977)] and later by Friedlander and Iwaniec [‘On Bombieri’s asymptotic sieve’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4)5(4) (1978), 719–756], as an application of the asymptotic sieve.

Let 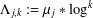$\unicode[STIX]{x1D6EC}_{j,k}:=\unicode[STIX]{x1D707}_{j}\ast \log ^{k}$, where 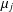$\unicode[STIX]{x1D707}_{j}$ denotes the Liouville function for 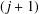$(j+1)$-free integers, and 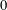$0$ otherwise. In this paper we evaluate the average value of 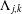$\unicode[STIX]{x1D6EC}_{j,k}$ in a residue class 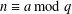$n\equiv a\text{ mod }q$, 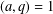$(a,q)=1$, uniformly on 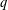$q$. When 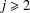$j\geq 2$, we find that the average value in a residue class differs by a constant factor from the expected value. Moreover, an explicit formula of Weil type for 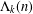$\unicode[STIX]{x1D6EC}_{k}(n)$ involving the zeros of the Riemann zeta function is derived for an arbitrary compactly supported 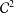${\mathcal{C}}^{2}$ function.

Keywords

Siegel–WalfiszSelberg’s theoremuniform asymptotic formulaDirichletL-functionWeil explicit formulageneralized Möbius functiongeneralized von Mangoldt function

MSC classification

Primary: 11M20: Real zeros of $L(s, chi)$; results on $L(1, chi)$ 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses 11N37: Asymptotic results on arithmetic functions
Secondary: 11M36: Selberg zeta functions and regularized determinants; applications to spectral theory, Dirichlet series, Eisenstein series, etc. Explicit formulas
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 111 , Issue 1 , August 2021 , pp. 127 - 144
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by I. Shparlinski

References

Bombieri, E., Le grand crible dans la théorie analytique des nombres, Astérisque, Vol. 18 (Société Mathématique de France, Paris, 1974).Google Scholar
Bombieri, E., ‘The asymptotic sieve’, Rend. Accad. Naz. XL (5) 1(2) (1975/76), 243–269; (1977).Google Scholar
Bombieri, E., ‘On twin almost primes’, Acta Arith. 28(2) (1975/76), 177–193.Google Scholar
Calderón, C., ‘Selberg’s inequality in arithmetic progressions. II’, Liet. Mat. Rink. 35(1) (1995), 23–36.Google Scholar
Calderón, C. and Zárate, M. J., ‘A generalization of Selberg’s asymptotic formula’, Arch. Math. (Basel) 56(5) (1991), 465–470.Google Scholar
Davenport, H., Multiplicative Number Theory, Vol. 72 (Markham Publishing Company, Chicago, 1967).Google Scholar
Farmer, D. W., Gonek, S. M. and Lee, Y., ‘Pair correlation of the zeros of the derivative of the Riemann 𝜉-function’, J. Lond. Math. Soc. (2) 90(1) (2014), 241–269.Google Scholar
Flajolet, P. and Sedgewick, R., Analytic Combinatorics (Cambridge University Press, Cambridge, 2009).Google Scholar
Friedlander, J. B., ‘Selberg’s formula and Siegel’s zero’, in: Recent Progress in Analytic Number Theory, Vol. 1 (Durham, 1979) (Academic Press, London, 1981), 15–23.Google Scholar
Friedlander, J. B. and Iwaniec, H., ‘On Bombieri’s asymptotic sieve’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 5(4) (1978), 719–756.Google Scholar
Ivić, A., ‘On the asymptotic formulas for a generalization of von Mangoldt’s function’, Rend. Mat. (6) 10(1) (1977), 51–59.Google Scholar
Knafo, E., ‘On a generalization of the Selberg formula’, J. Number Theory 125(2) (2007), 319–343.Google Scholar
Levinson, N., ‘A variant of the Selberg inequality’, Proc. Lond. Math. Soc. 14a(3) (1965), 191–198.Google Scholar
Pratt, K. and Robles, N., ‘Perturbed moments and a longer mollifier for critical zeros of 𝜁’, Res. Number Theory 4(9) (2018).Google Scholar
Pratt, K., Robles, N., Zeindler, D. and Zaharescu, A., ‘More than five-twelfths of the zeros of 𝜁 are on the critical line’, Res. Math. Sci. 7(2) (2020), Article 2.Google Scholar
Robles, N., Roy, A. and Zaharescu, A., ‘Twisted second moments of the Riemann zeta-function and applications’, J. Math. Anal. Appl. 434(1) (2016), 271–314.Google Scholar
Roy, A., ‘Unnormalized differences of the zeros of the derivative of the completed $L$ -function’, Preprint.Google Scholar
Selberg, A., ‘An elementary proof of the prime-number theorem’, Ann. of Math. (2) 50 (1949), 305–313.Google Scholar
Selberg, A., ‘An elementary proof of the prime-number theorem for arithmetic progressions’, Canad. J. Math. 2 (1950), 66–78.Google Scholar
Shapiro, H. N., ‘On primes in arithmetic progressions. I’, Ann. of Math. (2) 52 (1950), 217–230.Google Scholar
Siegel, C. L., ‘Über die Classenzahl quadratischer Zahlkörper’, Acta Arith. 1 (1935), 83–86.Google Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-Function, 2nd edn (ed. Heath-Brown, D. R.) (Clarendon Press, Oxford, 1986).Google Scholar
Walfisz, A., ‘Zur additiven Zahlentheorie. II’, Math. Z. 40(1) (1936), 592–607.Google Scholar
Weil, A., ‘Sur les “formules explicites” de la théorie des nombres premiers’, Comm. Sém. Math. Univ. Lund [Medd. Lunds Univ. Mat. Sem.] 1952 (1952), 252–265 (in French).Google Scholar