Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T00:45:13.063Z Has data issue: false hasContentIssue false
  • English
  • Français

UNKNOTTING TUNNELS, BRACELETS AND THE ELDER SIBLING PROPERTY FOR HYPERBOLIC 3-MANIFOLDS

Part of: Low-dimensional topology

Published online by Cambridge University Press:  07 June 2013

COLIN ADAMS  and
KARIN KNUDSON
COLIN ADAMS*
Affiliation:
Department of Mathematics and Statistics, Williams College, Williamstown, MA 01267 USA
KARIN KNUDSON
Affiliation:
Department of Mathematics, University of Texas, 1 University Station C1200, Austin, TX 78712 USA email kknudson@math.utexas.edu
*
✉Colin.C.Adams@williams.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An unknotting tunnel in a 3-manifold with boundary is a properly embedded arc, the complement of an open neighborhood of which is a handlebody. A geodesic with endpoints on the cusp boundary of a hyperbolic 3-manifold and perpendicular to the cusp boundary is called a vertical geodesic. Given a vertical geodesic $\alpha $ in a hyperbolic 3-manifold 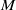$M$, we find sufficient conditions for it to be an unknotting tunnel. In particular, if $\alpha $ corresponds to a 4-bracelet, 5-bracelet or 6-bracelet in the universal cover and has short enough length, it must be an unknotting tunnel. Furthermore, we consider a vertical geodesic $\alpha $ that satisfies the elder sibling property, which means that in the universal cover, every horoball except the one centered at 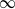$\infty $ is connected to a larger horoball by a lift of $\alpha $. Such an $\alpha $ with length less than 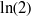$\ln (2)$ is then shown to be an unknotting tunnel.

Keywords

hyperbolic 3-manifoldunknotting tunnel

MSC classification

Secondary: 57M50: Geometric structures on low-dimensional manifolds
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 1 , August 2013 , pp. 1 - 19
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Adams, C., ‘Unknotting tunnels in hyperbolic 3-manifolds’, Math. Ann. 302 (1995), 177–195.CrossRefGoogle Scholar
Adams, C. and Reid, A., ‘Unknotting tunnels in two-bridge knot and link complements’, Comment. Math. Helv. 71 (4) (1996), 617–627.CrossRefGoogle Scholar
Agol, I., ‘Tameness of hyperbolic 3-manifolds’ (2004), arXiv:math.GT/0405568.Google Scholar
Calegari, D. and Gabai, D., ‘Shrinkwrapping and the taming of hyperbolic 3-manifolds’, J. Amer. Math. Soc. 19 (2) (2006), 385–446.CrossRefGoogle Scholar
Canary, R., ‘Marden’s tameness conjecture: history and applications’, in: Geometry, Analysis, and Topology of Discrete Groups, Advanced Lectures in Mathematics (ALM), 6 (2008), 137–162.Google Scholar
Cooper, D., Futer, D. and Purcell, J., ‘Dehn filling and the geometry of unknotting tunnels’ (2011), arXiv:1105.3461.Google Scholar
Cooper, D., Lackenby, M. and Purcell, J., ‘The length of unknotting tunnels’, Algebr. Geom. Topol. 10 (2) (2010), 637–661.CrossRefGoogle Scholar
Freedman, M. and McMullen, C., ‘Elder siblings and the taming of hyperbolic 3-manifolds’, Ann. Acad. Sci. Fenn. Math. 23 (2) (1998), 415–428.Google Scholar
Marden, A., ‘The geometry of finitely generated kleinian groups’, Ann. of Math. (2) 99 (2) (1974), 383–462.CrossRefGoogle Scholar
Mostow, G. D., ‘Quasi-conformal mappings in n-space and the rigidity of the hyperbolic space forms’, Publ. Math. Inst. Hautes Études Sci. 43 (1968).Google Scholar
Weeks, J., ‘SnapPea, A computer program for creating and studying hyperbolic 3-manifolds’, available at http://www.geometrygames.org/SnapPea.Google Scholar