Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beidar, K. I.
Latyshev, V. N.
Markov, V. T.
Mikhalev, A. V.
Skornyakov, L. A.
and
Tuganbaev, A. A.
1987.
Associative rings.
Journal of Soviet Mathematics,
Vol. 38,
Issue. 3,
p.
1855.
Agayev, Nazim
Çelik, Cesim
and
Özen, Tahire
2018.
On a generalization of semisimple modules.
Proceedings - Mathematical Sciences,
Vol. 128,
Issue. 2,


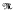 it is shown that the class
it is shown that the class 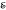 (
(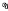 (
(