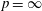Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
KEMPPAINEN, MIKKO
2016.
ON VECTOR-VALUED TENT SPACES AND HARDY SPACES ASSOCIATED WITH NON-NEGATIVE SELF-ADJOINT OPERATORS.
Glasgow Mathematical Journal,
Vol. 58,
Issue. 3,
p.
689.
Hong, Guixiang
Xu, Zhendong
and
Zhang, Hao
2025.
Best constants in the vector-valued Littlewood–Paley–Stein theory.
Mathematische Annalen,
Vol. 392,
Issue. 2,
p.
2533.