Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T15:32:40.951Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ZELEZNIKOW PROBLEM ON A CLASS OF ADDITIVELY IDEMPOTENT SEMIRINGS

Part of: Ordered structures Generalizations Semigroups

Published online by Cambridge University Press:  05 September 2013

YONG SHAO ,
SINIŠA CRVENKOVIĆ  and
MELANIJA MITROVIĆ
YONG SHAO
Affiliation:
Department of Mathematics, Northwest University of China, 1 Xuefu Road Changan, 710127 Xi’an, PR China email yongshaomath@gmail.com
SINIŠA CRVENKOVIĆ
Affiliation:
Department of Mathematics and Informatics, University of Novi Sad, 14 D. Obradovića, 21000 Novi Sad, Serbia email sima@eunet.rs
MELANIJA MITROVIĆ*
Affiliation:
Faculty of Mechanical Engineering, University of Niš, 14 A. Medevedeva, 18000 Niš, Serbia
*
✉meli@masfak.ni.ac.rs
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A semiring is a set 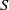$S$ with two binary operations $+ $ and $\cdot $ such that both the additive reduct 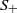${S}_{+ } $ and the multiplicative reduct 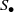${S}_{\bullet } $ are semigroups which satisfy the distributive laws. If 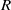$R$ is a ring, then, following Chaptal [‘Anneaux dont le demi-groupe multiplicatif est inverse’, C. R. Acad. Sci. Paris Ser. A–B 262 (1966), 274–277], 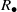${R}_{\bullet } $ is a union of groups if and only if 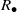${R}_{\bullet } $ is an inverse semigroup if and only if 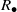${R}_{\bullet } $ is a Clifford semigroup. In Zeleznikow [‘Regular semirings’, Semigroup Forum 23 (1981), 119–136], it is proved that if 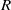$R$ is a regular ring then 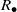${R}_{\bullet } $ is orthodox if and only if 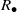${R}_{\bullet } $ is a union of groups if and only if 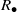${R}_{\bullet } $ is an inverse semigroup if and only if 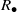${R}_{\bullet } $ is a Clifford semigroup. The latter result, also known as Zeleznikow’s theorem, does not hold in general even for semirings 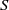$S$ with 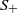${S}_{+ } $ a semilattice Zeleznikow [‘Regular semirings’, Semigroup Forum 23 (1981), 119–136]. The Zeleznikow problem on a certain class of semirings involves finding condition(s) such that Zeleznikow’s theorem holds on that class. The main objective of this paper is to solve the Zeleznikow problem for those semirings 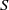$S$ for which 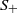${S}_{+ } $ is a semilattice.

Keywords

semiringamenable orderregular ordered semigrouporthodox semigroupinverse semigroupClifford semigroup

MSC classification

Secondary: 16Y60: Semirings 06F05: Ordered semigroups and monoids 20M18: Inverse semigroups 20M19: Orthodox semigroups
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 95 , Issue 3 , December 2013 , pp. 404 - 420
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Blyth, T. S., ‘Dubreil–Jacotin inverse semigroups’, Proc. Roy. Soc. Edinburgh (A) 71 (1973), 345–360.Google Scholar
Blyth, T. S., Lattices and Ordered Algebraic Structures (Springer, London, 2005).Google Scholar
Blyth, T. S. and Almeida Santos, M. H., ‘Amenable orders on orthodox semigroups’, J. Algebra 169 (1994), 49–70.CrossRefGoogle Scholar
Blyth, T. S. and Almeida Santos, M. H., ‘Amenable orders associated with inverse transversals’, J. Algebra 240 (2001), 143–169.CrossRefGoogle Scholar
Blyth, T. S. and Almeida Santos, M. H., ‘On amenable orders and inverse transversals’, Comm. in Algebra (6) 39 (2011), 2189–2209.CrossRefGoogle Scholar
Chaptal, N., ‘Anneaux dont le demi-groupe multiplicatif est inverse’, C. R. Acad. Sci. Paris Ser. A–B 262 (1966), 274–277.Google Scholar
Głazek, K., A Guide to the Literature on Semirings and Their Applications in Mathematics and Information Sciences (Kluwer, Dordrecht, 2002).CrossRefGoogle Scholar
Golan, J. S., Semirings and Their Applications (Kluwer, Dordrecht, 1999).CrossRefGoogle Scholar
Golan, J. S., Power Algebras over Semirings (Kluwer, Dordrecht, 1999).CrossRefGoogle Scholar
Golan, J. S., Semirings and Affine Equations over Them (Kluwer, Dordrecht, 2003).CrossRefGoogle Scholar
Howie, J. M., Fundamentals of Semigroup Theory (Oxford University Press, Oxford, 1995).CrossRefGoogle Scholar
McAlister, D. B., ‘Amenably ordered inverse semigroup’, J. Algebra 65 (1980), 118–146.CrossRefGoogle Scholar
McAlister, D. B. and Blyth, T. S., ‘Split orthodox semigroups’, J. Algebra 51 (1978), 491–525.CrossRefGoogle Scholar
McFadden, R., ‘Proper Dubreil–Jacotin inverse semigroups’, Glasg. Math. J. 16 (1975), 40–51.CrossRefGoogle Scholar
McKenzie, N. R. and Romanowska, A., ‘Varieties of $\cdot $-distributive bisemilattices, contributions of general algebra’, in: Proc. Klagenfurt Conference (Verlag Johannes Hegn, Klagenfurt, 1978), 213–218.Google Scholar
Pastijn, F. and Zhao, X. Z., ‘Green’s $ \mathcal{D} $-relation for the multiplicative reduct of an idempotent semiring’, Arch. Math. 36 (2000), 77–93.Google Scholar
Petrich, M., Inverse Semigroups (Wiley, New York, 1984).Google Scholar
Petrich, M. and Reilly, N. R., Completely Regular Semigroups (Wiley, New York, 1995).Google Scholar
Sen, M. K., Guo, Y. Q. and Shum, K. P., ‘A class of idempotent semirings’, Semigroup Forum 60 (2000), 351–367.Google Scholar
Sen, M. K. and Maity, S. K., ‘A note on orthodox additive inverse semirings’, Acta Univ. Palack. Olomuc., Fac. Rerum Natur. Math. (1) 43 (2004), 149–154.Google Scholar
Vandiver, H. S., ‘Note on simple type of algebra in which cancellation law of addition does not hold’, Bull. Amer. Math. Soc. 40 (1934), 914–920.CrossRefGoogle Scholar
Zeleznikow, J., ‘Orthodox semirings and rings’, J. Aust. Math. Soc. (Ser. A) 30 (1980), 50–54.CrossRefGoogle Scholar
Zeleznikow, J., ‘Regular semirings’, Semigroup Forum 23 (1981), 119–136.CrossRefGoogle Scholar