Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T02:16:42.042Z Has data issue: false hasContentIssue false
  • English
  • Français

ZEROS OF THE ESTERMANN ZETA FUNCTION

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  01 March 2013

A. DUBICKAS ,
R. GARUNKŠTIS ,
J. STEUDING  and
R. STEUDING
A. DUBICKAS*
Affiliation:
Department of Mathematics and Informatics, Vilnius University, Naugarduko 24, LT-03225 Vilnius, Lithuania
R. GARUNKŠTIS
Affiliation:
Department of Mathematics and Informatics, Vilnius University, Naugarduko 24, LT-03225 Vilnius, Lithuania email ramunas.garunkstis@mif.vu.lt
J. STEUDING
Affiliation:
Department of Mathematics, University of Würzburg, Am Hubland, Campus-Nord, Emil Fischer Str. 40, 97074 Würzburg, Germany email steuding@mathematik.uni-wuerzburg.de
R. STEUDING
Affiliation:
Department of Mathematics, University of Würzburg, Am Hubland, Campus-Nord, Emil Fischer Str. 40, 97074 Würzburg, Germany email rasa.steuding@mathematik.uni-wuerzburg.de
*
✉arturas.dubickas@mif.vu.lt
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we investigate the zeros of the Estermann zeta function 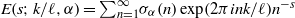$E(s; k/ \ell , \alpha )= { \mathop{\sum }\nolimits}_{n= 1}^{\infty } {\sigma }_{\alpha } (n) \exp (2\pi ink/ \ell ){n}^{- s} $ as a function of a complex variable $s$, where 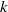$k$ and 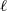$\ell $ are coprime integers and 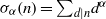${\sigma }_{\alpha } (n)= {\mathop{\sum }\nolimits}_{d\vert n} {d}^{\alpha } $ is the generalized divisor function with a fixed complex number $\alpha $. In particular, we study the question on how the zeros of 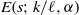$E(s; k/ \ell , \alpha )$ depend on the parameters 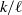$k/ \ell $ and $\alpha $. It turns out that for some zeros there is a continuous dependency whereas for other zeros there is not.

Keywords

Estermann zeta functiondistribution of zerostrajectories of zeros

MSC classification

Secondary: 11M41: Other Dirichlet series and zeta functions
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 94 , Issue 1 , February 2013 , pp. 38 - 49
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Balanzario, E. P. and Sánchez-Ortiz, J., ‘Zeros of the Davenport–Heilbronn counterexample’, Math. Comp. 76 (2007), 2045–2049.CrossRefGoogle Scholar
Chandrasekharan, K., Introduction to Analytic Number Theory (Springer, Berlin, 1968).CrossRefGoogle Scholar
Estermann, T., ‘On the representation of a number as the sum of two products’, Proc. Lond. Math. Soc. 31 (1930), 123–133.CrossRefGoogle Scholar
Garunkštis, R. et al. , ‘On zeros of the Lerch zeta-function. II’, in: Probability Theory and Mathematical Statistics: Proceedings of the Seventh Vilnius Conf. (1998), (ed. Grigelionis, B.) (TEV/Vilnius, VSP/Utrecht,, 1999), 267–276.Google Scholar
Garunkštis, R., Laurinčikas, A., Šleževičienė, R. and Steuding, J., ‘On the universality of Estermann zeta-functions’, Analysis 22 (2002), 285–296.CrossRefGoogle Scholar
Garunkštis, R. and Steuding, J., ‘On the distribution of zeros of the Hurwitz zeta-function’, Math. Comp. 76 (2007), 323–337.CrossRefGoogle Scholar
Kiuchi, I., ‘On an exponential sum involving the arithmetic function ${\sigma }_{a} (n)$’, Math. J. Okayama Univ. 29 (1987), 193–205.Google Scholar
Laurinčikas, A. and Garunkštis, R., The Lerch Zeta-function (Kluwer Academic Publishers, Dordrecht, 2002).Google Scholar
Littlewood, J. E., ‘On the zeros of the Riemann zeta-function’, Proc. Camb. Phil. Soc. 22 (1924), 295–318.CrossRefGoogle Scholar
Šleževičienė, R. and Steuding, J., ‘On the zeros of the Estermann zeta-function’, Int. Trans. Spec. Funct. 13 (2002), 363–371.CrossRefGoogle Scholar
Steuding, J., Value-Distribution of L-functions, Lecture Notes in Mathematics, 1877 (Springer, New York, 2007).Google Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-function, 2nd edn (Oxford University Press, Oxford, 1986), revised by D. R. Heath-Brown.Google Scholar