Let IE, ∧ and ∧R denote the collections of all non-negative integers, isols and regressive isols respectively. An ω-group is a pair (α, p) where (1) α ⊆ E, (2) p(x, y) is a partial recursive group multiplication for α and (3) the function which maps each element of α to its inverse under p has a partial recursive extension. If G = (α, p) is an ω-group, we call the recursive equivalence type of a the RET or order of G (written o(G)). Let GR = {T∈∧R′T = o(G) for some ω-group G}. It follows from the version of the Lagrange Theorem given in [4] that ∧R − GR is non-empty and has cardinality c. In this paper we characterise the isols in GR as follows: A regressive isol T belongs to GR if and only if T∈E or T is infinite and there exist a regressive isol U ≦ T and a function an from E into E − {0} such that U ≦*an and T = ΠUan. (The “≦*” is denned in [2]). In presenting the proof of this result, we shall assume that the reader is familiar with either [3] or [4]. The proof that, given an and U ≦*an, a group of order ΠUan exists is based on the natural trick—one constructs a direct product of disjoint cyclic groups of order a0, a1,… indexed by elements of a set of RET U. The proof that any regressive group G has order of the form ΠUan is trivial for finite groups; the proof for infinite regressive groups is based upon the construction of an ascending chain of finite subgroups Gi of G such that 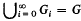 and
and 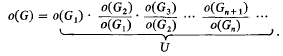 .
.
 e
e