1 Introduction
Time preferences are arguably the most important factor of sequential-bargaining models. A patient player has more bargaining power than her less patient opponent because her cost of delay in case of disagreement is lower.
There are many ways of implementing discounting in an experiment. One of the canonical methodologies is the shrinking-pie procedure in which the value the players bargain over (the pie) is reduced between rounds. A newer alternative is the effective-discounting procedure implemented in an infinite-time setting by Kim et al. (Reference Kim, Lim and Schweighofer-Kodritsch2023), where disagreement leads to payment being delayed into the future. Both the shrinking-pie and the effective-discounting procedures are attempts at implementing the real-time costs of delaying bargaining in an experimental setting. An alternative is to let substantial time pass between bargaining rounds in the experiment. We call this novel approach the bargaining-delay procedure.
There is currently a dearth of comparisons between discounting methodologies in bargaining experiments, although (Fréchette & Yuksel, Reference Fréchette and Yuksel2017) directly compare implementations in cooperation games. Comparisons of methodologies serve several useful purposes. Social preferences may be activated to different degrees with different methodologies and documenting differences in outcomes may aid comparisons of results between studies. Related, some types of discounting may be more compelling than others to subjects in the lab, resulting in different outcomes. Furthermore, as Fréchette and Yuksel (Reference Fréchette and Yuksel2017) discuss, different contexts may motivate different discounting procedures, so understanding potential practical and empirical differences are crucial.
This paper tests and compares different discounting methodologies in bargaining games. We report the impact of different discounting implementations in alternating-offer bargaining experiments. We conduct treatments with three different discounting implementations; the shrinking-pie procedure, the effective-discounting procedure and the bargaining-delay procedure.Footnote 1 We follow the canonical Ochs and Roth framework closely. We chose this framework because it serves as a simple benchmark for the comparison of discounting methodologies and ensures some comparability with the complete information framework of Kim et al. (Reference Kim, Lim and Schweighofer-Kodritsch2023).Footnote 2
There is a clear trade-off between realism and control in the three discounting procedures we test. In the shrinking-pie procedure the discount factor is tightly controlled, but is the most removed from the real life delay it represents. The effective-discounting procedure introduces payment delay into bargainers payoffs, but although the length of delay is controlled and is common knowledge, control over individual patience and discount factors and bargainers beliefs is lost. The bargaining-delay procedure is an additional step towards realism, as actual delay is incorporated into the bargaining process itself, rather than just the payoffs. This comes at the cost of necessitating an online experiment with a less controlled environment.
The literature has found no sensitivity to discount factors and number of periods in classic sequential-bargaining models in the lab, finding instead behavioral responses where the modal response is 50–50 and lower offers are rejected with positive frequency (Binmore et al., Reference Binmore, Swierzbinski and Tomlinson2007; Camerer et al., Reference Camerer, Johnson, Rymon and Sen1993; Ochs & Roth, Reference Ochs and Roth1989; Rapoport et al., Reference Rapoport, Weg and Felsenthal1990; Weg et al., Reference Weg, Rapoport and Felsenthal1990; Zwick et al., Reference Zwick, Rapoport and Howard1992). In particular, Ochs and Roth (Reference Ochs and Roth1989) reject predictions of the finite-time alternating-offers model, finding no sensitivity to time preferences (discount factors) or the number of periods in the game. In line with Güth et al. (Reference Güth, Schmittberger and Schwarze1982), these findings set the stage for a large literature on ”Other Regarding Preferences” (ORP) in order to explain the behavioral responses in such lab experiments (Andreoni, Reference Andreoni1990; Fehr & Schmidt, Reference Fehr and Schmidt1999; Fehr & Fischbacher, Reference Fehr and Fischbacher2002).Footnote 3 Kim et al. (Reference Kim, Lim and Schweighofer-Kodritsch2023) find comparative statics that broadly support the theoretical predictions of Rubinstein (Reference Rubinstein1982) when using the effective-discounting procedure.
While discount factors has largely produced negative results, the modern bargaining literature has been more positive, with recent frameworks often focusing on unstructured real-time bargaining, see Camerer et al. (Reference Camerer, Nave and Smith2019), Karagözoğlu and Kocher (Reference Karagözoğlu and Kocher2019) and Bochet et al. (Reference Bochet, Khanna and Siegenthaler2020). Using field data from an online marketplace, Backus et al. (Reference Backus, Blake, Larsen and Tadelis2020) document bargaining behavior consistent with the theoretical predictions of an incomplete information bargaining model, but they also find evidence of bargaining patterns consistent with behavioral factors such as reciprocity in addition to supporting the split-the-difference behavioral norm. Keniston et al. (Reference Keniston, Larsen, Li, Prescott, Silveira and Yu2021) gather data from a range of real-world sources and document the split-the-difference norm's prevalence. Fanning and Kloosterman (Reference Fanning and Kloosterman2022) find strong support for theoretical predictions of the Coase conjecture in an infinite-horizon environment.
We start out by revisiting Ochs and Roth's (1989) original study where discounting is implemented by the shrinking-pie procedure. Our main treatment measure is the first-period offer, which is tested with four empirical approaches. Our primary test is the Wilcoxon rank sum test, which is complimented by regression analysis, Kolmogorov–Smirnov (KS) distributional tests and Barrett and Donald (Reference Barrett and Donald2003) (BD) first-order stochastic dominance tests. First, we vary the number of periods played in a game, keeping discount factors constant. The model predicts that going from two to three periods should decrease the first-period proposer's offer because she is also the proposer in the last period in the three-period game (as opposed to in the two-period game). As in Ochs and Roth (Reference Ochs and Roth1989), this prediction fails to materialize in our data. Second, we increase the discount factor of the first-period responder. The model also predicts that making the first-period responder more patient should increase the first-period offer because the proposer has to offer more to make her opponent indifferent between accepting the offer or going to the next round. We partially replicate Ochs and Roth's findings in this matter as we do not find a clear treatment difference of this change in the discount factor with the rank sum test, and while this is supported by regression analysis, both the KS and BD tests show a significant difference in the direction predicted by the model. Average first-period offers in these treatments are in the range of 42–45 percent of the pie, close to a 50–50 split, and rejection rates are in the range of 0.12–0.23.
We then repeat the same treatments as above with the only difference that we implement discounting using the effective-discounting procedure. That is, if an offer is rejected and bargaining goes on to a new round, payments are deferred by 1 week or 1 month. One week is meant to represent a high discount factor while 1 month is meant to represent a low discount factor. Again, we do not find any treatment differences when changing the number of bargaining rounds from two to three. On the other hand, we do find a treatment difference when changing payment deferrals for the first-period responder from 1 week to 1 month in the rank sum test. This is supported by the BD test which finds a significant difference between treatments. However, the regression analysis and the KS distributional test do not. As with the shrinking-pie procedure, first-period offers in treatments with effective discounting are in the range of 45–50 percent of the pie, again close to a 50–50 split. Furthermore, rejection rates are quite high, ranging from 0.28 to 0.36. Overall we find that the effective-discounting procedure performs similarly to the shrinking-pie procedure in our finite-time bargaining environment.
We then implement the bargaining-delay procedure in an online experiment. We use an online experiment rather than a lab experiment for this procedure because we believe it better addresses the issues of attrition and transaction costs between bargaining rounds. In the online experiment, we delay bargaining between rounds by periods of 1 week and vary the number of periods in a game. We find no treatment effect, and in line with the other treatments, first-period offers are in the 43–45 percent range. We also find high rejection rates, with results in the 0.29–0.36 range. That is, the bargaining-delay procedure seems to induce bargaining behavior similar to that of the shrinking-pie and the effective-discounting procedures.
2 Model
There are two players,
![]() and two or three periods (bargaining rounds). In the first period, player 1 chooses an offer
and two or three periods (bargaining rounds). In the first period, player 1 chooses an offer
![]() where the total amount bargained over (the pie) is normalized to 1. Player 2 may accept or reject this offer. If player 2 accepts, then the game ends and players receive
where the total amount bargained over (the pie) is normalized to 1. Player 2 may accept or reject this offer. If player 2 accepts, then the game ends and players receive
![]() . If player 2 rejects, the game proceeds to the next round. In the next round, the pie is discounted according to each player's individual discount factor
. If player 2 rejects, the game proceeds to the next round. In the next round, the pie is discounted according to each player's individual discount factor
![]() , and player 2 makes an offer
, and player 2 makes an offer
![]() which player 1 may accept or reject. If player 1 accepts, the game ends and players receive
which player 1 may accept or reject. If player 1 accepts, the game ends and players receive
![]() . If player 1 rejects and there are only two periods, the game ends and players receive (0, 0). If player 1 rejects and there are three periods, the game moves to the last round where player 1 again makes an offer
. If player 1 rejects and there are only two periods, the game ends and players receive (0, 0). If player 1 rejects and there are three periods, the game moves to the last round where player 1 again makes an offer
![]() . If the offer is accepted, then the game ends and players receive
. If the offer is accepted, then the game ends and players receive
![]() while if player 2 rejects, the game ends and players receive (0, 0).
while if player 2 rejects, the game ends and players receive (0, 0).
We here give a brief intuition of the subgame perfect Nash equilibrium of the game. Subgame perfection implies that the optimal offer in a round makes the receiving player indifferent between accepting that round's offer or moving to the next period and getting her anticipated payoff net of discounting. In the last period, the game turns into an Ultimatum game, where the equilibrium offer is 0, which is accepted by the responder. The equilibrium offers are calculated as follows (see Table 1).
Table 1 Equilibrium offers

|
Offer |
2-period game |
3-period game |
|---|---|---|
|
1st period |
|
|
|
2nd period |
0 |
|
|
3rd period |
N/A |
0 |
In the experiment, we focus on the following predictions of the model:
1. Increasing the periods from two to three decreases the first-period offer;
2. Increasing Player 2's discount factor increases the first-period offer;
2.1 Modeling assumptions
The two equilibrium predictions above are robust to a range of preferences. The model assumes that individuals only have preferences over their own monetary payoff. This is at odds with the existence of ORP, which are well-established in the experimental literature (Burrows & Loomes, Reference Burrows, Loomes and Hey1994; Birkeland & Tungodden, Reference Birkeland and Tungodden2014; De Bruyn & Bolton, Reference De Bruyn and Bolton2008; Fehr & Schmidt, Reference Fehr and Schmidt1999). Including such ORP would impact point predictions, but would not affect the comparative statics we focus on.
Present bias has been widely documented and is at odds with the assumption of exponential discounting (Imai et al., Reference Imai, Rutter and Camerer2021). Including different types of discounting would impact point predictions, however, the comparative static predictions are unaffected.Footnote 4
We follow Kim et al. (Reference Kim, Lim and Schweighofer-Kodritsch2023) and assume complete information in our framework. This assumption predicts agreement in the first period. There is of course the potential for some individual heterogeneity in discount factors, behavioral types and beliefs across individuals; however, we focus exclusively on group-level analysis and assume that these underlying heterogeneous elements are constant across treatments. As in Kim et al. (Reference Kim, Lim and Schweighofer-Kodritsch2023), we find no differences between rejection rates across treatments within procedures and take this as evidence that incomplete information effects are constant within procedures.
3 Design and procedures
In our experiment, we implement an alternating-offers bargaining protocol to match the model presented above. The aim of our design is to examine whether different procedures of implementing discounting affect experimental results from the bargaining game. In this section, we lay out the design and procedures for the main treatments, where we employ the traditional shrinking-pie procedure and the new effective-discounting procedure. The design (and results) of treatments using the bargaining-delay procedure is deferred until Sect. 5.
We conduct six main treatments, S3A, S2A, S2S, E3A, E2A, and E2S. The first three treatments are pure replications of Ochs and Roth (Reference Ochs and Roth1989) (treatments given by Cell 2, Cell 3 and Cell 6) where we have followed their methodology as closely as possible. Treatments E3A, E2A and E2S follow the same procedure except we replace the shrinking-pie procedure with the effective-discounting procedure from Kim et al. (Reference Kim, Lim and Schweighofer-Kodritsch2023) and include a time-preference elicitation exercise. In the effective discount procedure, if agreement is not reached, then actual payments from the experiment are deferred to actual future dates.Footnote 5 Treatments are named after their method, shrinking-pie or effective-discounting, the number of periods, two or three, and whether discount factors are symmetric or asymmetric. Our treatments are summarized in Table 2.
Table 2 Main treatments

|
Treatment |
Periods |
Proposer
|
Responder
|
Equilibrium offer |
|---|---|---|---|---|
|
S3A |
3 |
.6 |
.4 |
16% |
|
S2A |
2 |
.6 |
.4 |
40% |
|
S2S |
2 |
.6 |
.6 |
60% |
|
E3A |
3 |
1 week |
1 month |
|
|
E2A |
2 |
1 week |
1 month |
|
|
E2S |
2 |
1 week |
1 week |
|
Equilibrium offers are reported as a percentage of the pie
Because E3A, E2A and E2S all rely on the real value of money in 1 week or 1 month, we need to perform an elicitation task to calculate equilibrium predictions. We used the simplest and most common elicitation task, the multiple price list (MPL) (Cohen et al., Reference Cohen, Ericson, Laibson and White2020; Andersen et al., Reference Andersen, Harrison, Lau and Rutström2006; Freeman et al., Reference Freeman, Manzini, Mariotti and Mittone2016). Elicitations of time preferences can vary based on method and population, and elicitations over a week and a month will almost certainly be higher than the .6 and .4 used in our replication treatments (Cohen et al., Reference Cohen, Ericson, Laibson and White2020; Frederick et al., Reference Frederick, Loewenstein and O’donoghue2002; Matousek et al., Reference Matousek, Havranek and Irsova2022). However, as can be seen from Table 2, equilibrium predictions are that there should be a treatment effect of changing the number of periods or the payment delay of Player 2. One of the weaknesses of the effective-discounting procedure is that we lose precise control of the discount factors. We are able to create public knowledge of the relative delays, but not the discount factors implied by these delay periods. See Kim et al. (Reference Kim, Lim and Schweighofer-Kodritsch2023) for a discussion of this point. In contrast to Kim et al. (Reference Kim, Lim and Schweighofer-Kodritsch2023), we do not include random termination probability, because we have a finite number of periods in this setup. Additionally, we do not include front-end delay for payments in any treatments.
Sessions were conducted in the Research Lab at BI Norwegian Business School in Oslo and at the LEE lab at the University of Copenhagen in the period 4/10/19 to 22/11/21.Footnote 6 The study was preregistered on 25/2/20 after an initial pilot was run.Footnote 7 Subjects were recruited from the general student populations of BI Norwegian Business School and the University of Copenhagen, respectively. Each subject participated in 10 bargaining games and we collected 5 blocks of 10 subjects per treatment, meaning a total of 50 subjects and 250 bargaining games per treatment. Each session contained between 10 and 30 subjects and no subject participated in more than one session. A total of 300 subjects participated in a total of 1500 bargaining games played. We implemented randomized matching within blocks. At the conclusion of a session, a random game was selected for each individual and earnings in an experimental currency unit (ECU) were converted to NOK/DKK at a publicly announced exchange rate. On average, subjects in the Norwegian sessions earned 31.4 EUR while subjects in the Danish sessions earned 20.0 EUR.Footnote 8 z-Tree was used to program and conduct the experiment (Fischbacher, Reference Fischbacher2007).
As in Ochs and Roth (Reference Ochs and Roth1989), we implemented fixed initial roles. The size of the pie was fixed at 100 points per player, and the exchange rate of point to ECU varied in treatments with the shrinking-pie procedure. When implementing the effective-discounting procedure, the exchange rate was constant but the date of payment varied. See Supplementary Information (SI) section B for more procedural details.
4 Results
We primarily focus on first-period offers, but we also consider first-period rejection rates. The Wilcoxon rank sum test is the primary empirical approach which we compliment with three additional approaches.Footnote 9 We report p-values from non-parametric (Wilcoxon) rank sum tests using matching block averages as units of observation (
![]() ). We supplement this with p-values from parametric treatment regressions using individual choices as units of observation with robust standard errors clustered at matching blocks (
). We supplement this with p-values from parametric treatment regressions using individual choices as units of observation with robust standard errors clustered at matching blocks (
![]() ). Both tests are two-sided. We also conduct Kolmogorov–Smirnov distributional tests (
). Both tests are two-sided. We also conduct Kolmogorov–Smirnov distributional tests (
![]() ) and first-order stochastic dominance tests using the method of Barrett and Donald (Reference Barrett and Donald2003) (
) and first-order stochastic dominance tests using the method of Barrett and Donald (Reference Barrett and Donald2003) (
![]() ) on participant mean first offers.Footnote 10 Details from all empirical tests, descriptive statistics from all periods, first-period offers and rejection rates by block, additional testing on the subsample of non-equal split initial offers and disadvantageous counteroffers, and a direct comparison to Ochs and Roth (Reference Ochs and Roth1989) can all be found in the SI section A. The results that follow are based on all games played in the experiment. We justify this choice with the absence of trends over games in our sample; see SI A.7 for a discussion of this choice and robustness checks.
) on participant mean first offers.Footnote 10 Details from all empirical tests, descriptive statistics from all periods, first-period offers and rejection rates by block, additional testing on the subsample of non-equal split initial offers and disadvantageous counteroffers, and a direct comparison to Ochs and Roth (Reference Ochs and Roth1989) can all be found in the SI section A. The results that follow are based on all games played in the experiment. We justify this choice with the absence of trends over games in our sample; see SI A.7 for a discussion of this choice and robustness checks.
4.1 Results for the shrinking-pie procedure
Our first main result is that we successfully replicate (Ochs & Roth, Reference Ochs and Roth1989) by showing that equilibrium predictions of the model fare poorly when compared with the data. This result can be seen in Fig. 1, which shows the average observed first-round offers and equilibrium predictions of the three treatments implementing discounting with the shrinking-pie procedure (S3A, S2A and S2S).
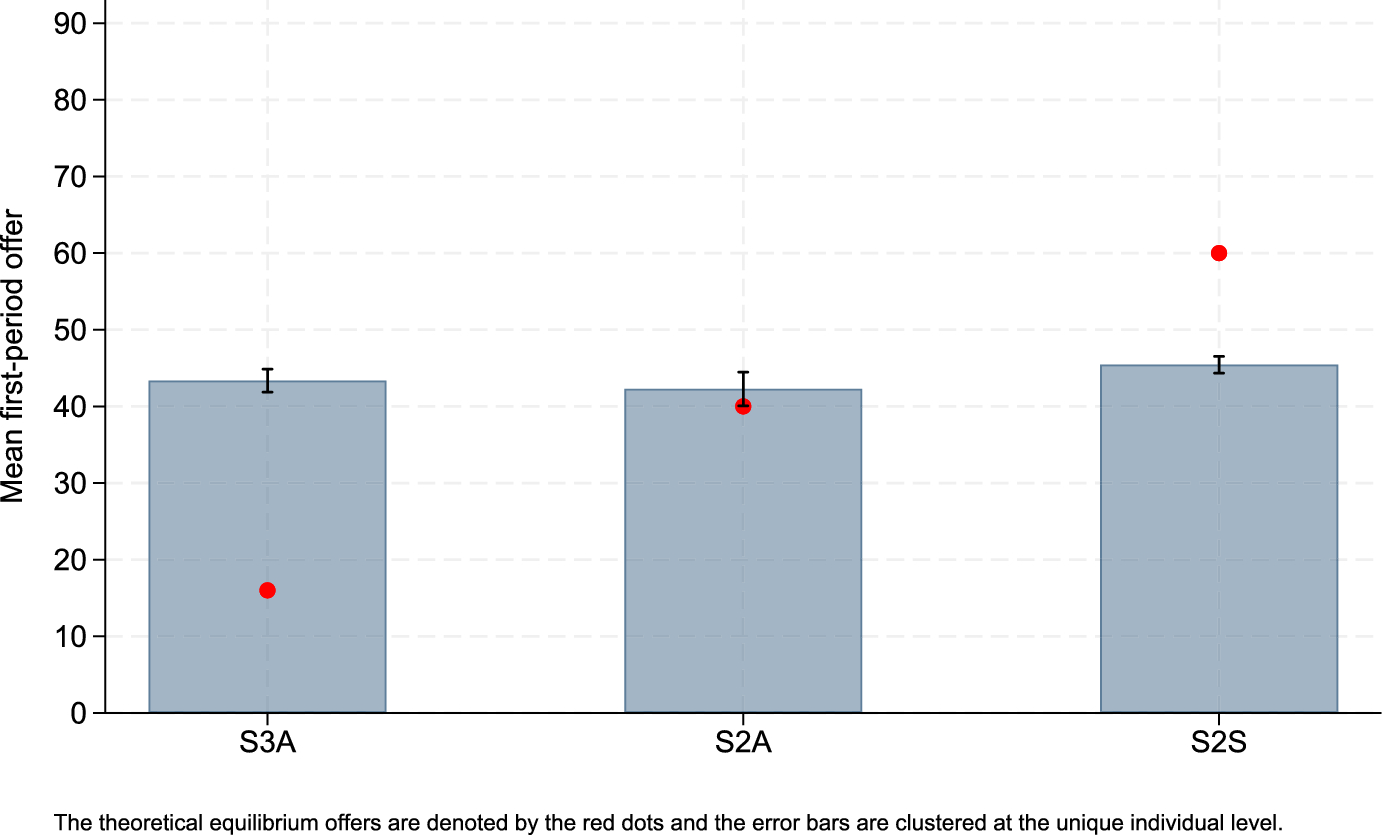
Fig. 1 Average first-period offers for S3A, S2A and S2S
We make two observations related to our main comparative statics. First, the model predicts that going from two to three periods should decrease the first-period offer, while the difference between S3A and S2A is non-significant in the non-parametric test (
![]() = 0.841). This is supported by all three complimentary tests (
= 0.841). This is supported by all three complimentary tests (
![]() = 0.497;
= 0.497;
![]() = 0.285;
= 0.285;
![]() = 0.132). Thus, we fail to reject the null that first-period offers in the three-period game in S3A are equal to those in the two-period game in S2A.
= 0.132). Thus, we fail to reject the null that first-period offers in the three-period game in S3A are equal to those in the two-period game in S2A.
Second, the model also predicts that increasing the discount factor of the first-period responder should increase the first-period offer. There is no significant difference between S2A and S2S using the non-parametric test (
![]() = 0.222) and this is supported by the parametric test (
= 0.222) and this is supported by the parametric test (
![]() = 0.083). However, this is not supported by the distributional tests where there is a significant difference between the distributions (
= 0.083). However, this is not supported by the distributional tests where there is a significant difference between the distributions (
![]() = 0.002;
= 0.002;
![]() = 0.000). Thus, we find partial support for a treatment effect.
= 0.000). Thus, we find partial support for a treatment effect.
We also note that equilibrium offers in the first period are 16 percent in S3A, 40 percent in S2A, and 60 percent in S2S, while observed average first-period offers are 43.4 percent in S3A, 42.3 percent in S2A, and 45.4 percent in S2S. That is, point predictions of the model do not seem to explain observational behavior well for S3A and S2S, while S2A is very close to its point prediction. One could argue that S3A and S2S are closer to a 50-50 split rule than the point predictions of the model and that the magnitude of treatment effects are small.
Last, we observe that first-round rejection rates are 0.13 in S3A, 0.12 in S2A and 0.23 in S2S. Although there is no information problem in the model, and we try to the best of our ability to implement a complete information environment in the experiment, subjects may of course bring beliefs about different unmodelled types with them into the lab. Our finding on delay, then, is consistent with bargaining models of incomplete information, for instance on the presence of obstinate bargaining types as in Embrey et al. (Reference Embrey, Fréchette and Lehrer2015) and Heggedal et al. (Reference Heggedal, Helland and Knutsen2022).
4.2 Results for the effective-discounting procedure
Our second main result is that the effective-discounting procedure yields similar results as the shrinking-pie procedure. This result can be seen in Fig. 2, which shows average observed first-round offers and equilibrium predictions of the three treatments using the effective-discounting procedure (E3A, E2A and E2S).
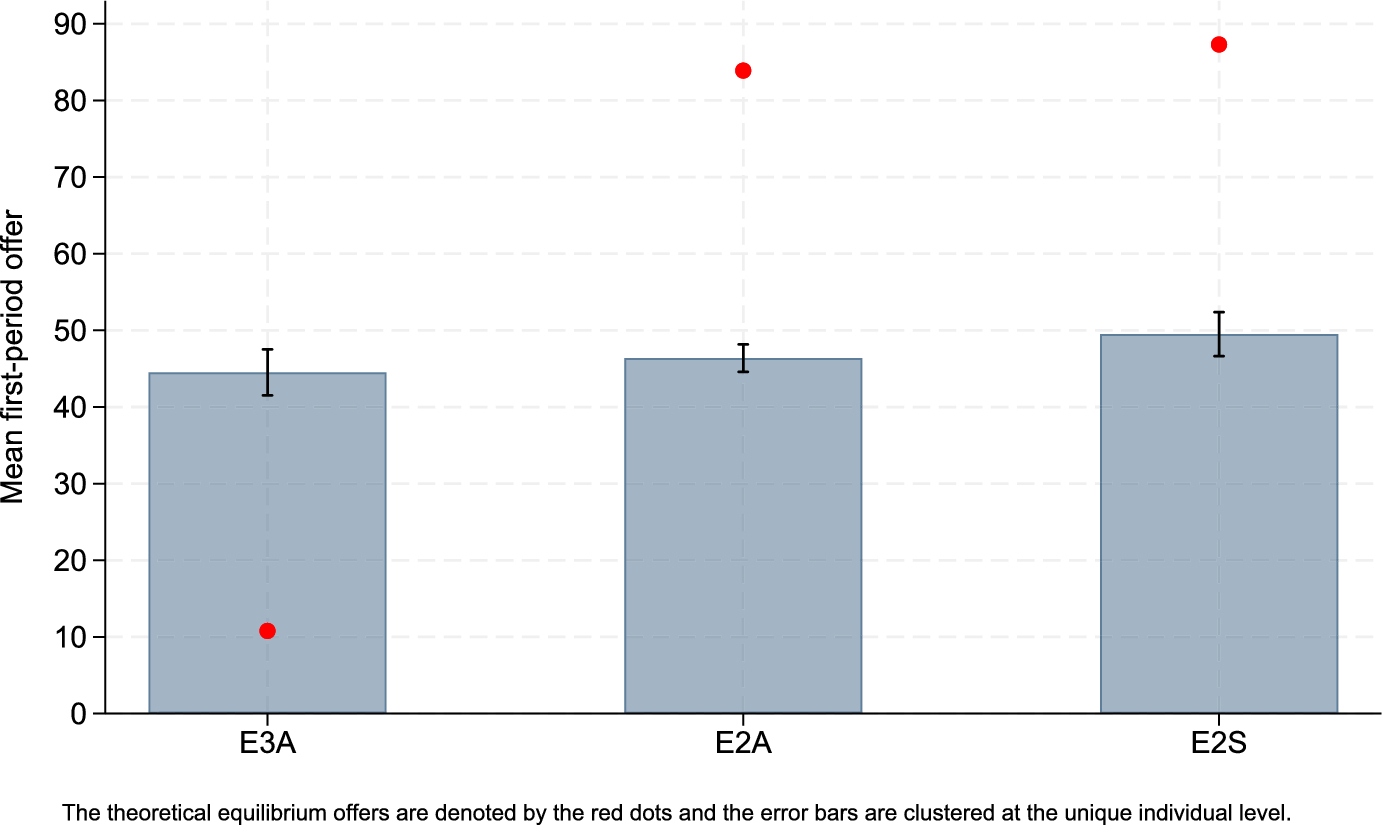
Fig. 2 Average first-period offers for E3A, E2A and E2S
We make two observations related to our main comparative statics. First, as with the shrinking-pie procedure, there is no significant difference between first-period offers in the three-period game in E3A and the two-period game in E2A in the non-parametric test (
![]() = 0.222) and this is supported by all three complimentary tests (
= 0.222) and this is supported by all three complimentary tests (
![]() = 0.269;
= 0.269;
![]() = 0.200;
= 0.200;
![]() = 0.151). This lack of a significant difference indicates that the number of periods has little effect on initial offers when using the effective-discounting procedure.
= 0.151). This lack of a significant difference indicates that the number of periods has little effect on initial offers when using the effective-discounting procedure.
Second, there is no treatment difference when changing payment deferrals for the first-period responder from 1 month in E2A to one week in E2S in the non-parametric test (
![]() = 0.056). This is supported by the KS test which is also not significant (
= 0.056). This is supported by the KS test which is also not significant (
![]() = 0.200). However, the parametric test and the stochastic dominance test do not support this result as both show significant differences (
= 0.200). However, the parametric test and the stochastic dominance test do not support this result as both show significant differences (
![]() = 0.049;
= 0.049;
![]() = 0.000). Also, both the parametric and non-parametric tests are very close to the 5% significance threshold.
= 0.000). Also, both the parametric and non-parametric tests are very close to the 5% significance threshold.
We also note that observed first-period offers are a long way from the point predictions of the model. To compute the equilibrium offers, we impute discount factors from elicited time preferences. This computation is done by taking the switching point chosen in the MPL and assuming the subjects are indifferent exactly between the two points at which they switch. The imputed deltas are then equal to the payment today divided by the payment in the future at these switching points. The average values are
![]() and
and
![]() .Footnote 11 The equilibrium offers are then 10.9 percent in E3A, 83.6 percent in E2A, and 87.0 percent in E2S, while observed average first-period offers are 44.5 percent in E3A, 46.4 percent in E2A, and 49.5 percent in E2S. As with the shrinking-pie procedure, we think it is fair to say that the observed offers are closer to a 50–50 split rule than the point predictions of the model.
.Footnote 11 The equilibrium offers are then 10.9 percent in E3A, 83.6 percent in E2A, and 87.0 percent in E2S, while observed average first-period offers are 44.5 percent in E3A, 46.4 percent in E2A, and 49.5 percent in E2S. As with the shrinking-pie procedure, we think it is fair to say that the observed offers are closer to a 50–50 split rule than the point predictions of the model.
Last, we observe that first-round rejection rates are quite high, with 0.36 in E3A, 0.28 in E2A, and 0.36 in E2S. These rates are higher than those in the treatments using the shrinking-pie procedure. Pooling treatments on discounting procedures, rejection rates in the effective-discounting treatments are significantly higher than those in the shrinking-pie treatments (
![]() = 0.000;
= 0.000;
![]() = 0.000). Because rejection is equivalent to inefficiency in this setting, the effective-discounting procedure elicits more inefficiency. For comparison, Ochs and Roth (Reference Ochs and Roth1989) reported a 15 percent rejection rate in the relevant treatments, whereas Kim et al. (Reference Kim, Lim and Schweighofer-Kodritsch2023) found rejection rates around 25 percent. These higher rejection rates may be the result of increased uncertainty for subjects about their opponents’ patience in the treatments that use the effective-discounting procedure.
= 0.000). Because rejection is equivalent to inefficiency in this setting, the effective-discounting procedure elicits more inefficiency. For comparison, Ochs and Roth (Reference Ochs and Roth1989) reported a 15 percent rejection rate in the relevant treatments, whereas Kim et al. (Reference Kim, Lim and Schweighofer-Kodritsch2023) found rejection rates around 25 percent. These higher rejection rates may be the result of increased uncertainty for subjects about their opponents’ patience in the treatments that use the effective-discounting procedure.
5 Bargaining-delay procedure
There are of course many ways to approach the real-time costs of delayed bargaining in experiments. In this section, we explore a bargaining-delay procedure in which substantial time passes between bargaining rounds in the experiment. That is, in an online experiment, we delay bargaining between rounds by periods of one week in case of rejections.Footnote 12 The aim is to test whether bargaining outcomes differ when introducing a real-time delay between bargaining rounds compared with bargaining immediately, but delaying payments into the future. This procedure focuses on prediction 1 of the model, that increasing the number of periods from two to three decreases the first period offer.Footnote 13
5.1 Design and procedures
Apart from the discounting procedure, the bargaining game in the online experiment is implemented as closely to the lab experiment as possible. We conducted two treatments, B3S and B2S, in the online experiment, summarized in Table 3.
Table 3 Additional treatments

|
Treatment |
Periods |
Proposer delay |
Responder delay |
Equilibrium offer |
|---|---|---|---|---|
|
B3S |
3 |
1 week |
1 week |
|
|
B2S |
2 |
1 week |
1 week |
|
Equilibrium offers are reported as a percentage of the pie
This online study had some notable changes from our main treatments. First, subjects were paid for each game they played, rather than randomly selecting a single game. This change was necessary because we cannot randomize across payments that occur at different times. In addition, all games were played concurrently, i.e., subjects played the first period of all games during session 1 and played all second (third) periods during session 2 (3). This is the only practical way to gather multiple observations for each subject. We also reduced the number of games from 10 to 5 for each subject. This reduction increases the incentive for returning for a single match and reduces potential attrition.
Block size remains constant with 10 subjects and fixed roles which means that each pair matched exactly once. We collected 5 blocks for each treatment. These treatments were programmed using oTree (Chen et al., Reference Chen, Schonger and Wickens2016). In the case of attrition, we automated responses based on the behavior of subjects in E2S and E3A, the most similar treatments. Treatments were conducted between 9/4/22 and 26/5/22 on Prolific. One hundred subjects participated in a total of 250 bargaining games. Each bargaining game had a total pie of $5 USD and the average payment per subject was $16.47 USD.Footnote 14 Each session took subjects approximately 6 min to complete and was implemented asynchronously. As is common practice in online experiments, we included three comprehension questions in the instructions, which subjects answered with a high degree of accuracy. Most matches were completed in the first round without automation (68.8 percent). Attrition was 42.4 percent and 52.8 percent in B3S and B2S, respectively.
Because B3S and B2S occurred over a series of weeks, we could not collect time elicitations on the day of the treatments without contaminating the incentives of subjects for the remaining rounds. Instead, we performed a follow-up study targeted directly at those who participated in B3S and B2S. This study had a 75 percent response rate and was used to calculate the equilibrium offers for these treatments. See SI section C for additional details regarding technical implementation, automation of responses in the case of attrition, timeline of experiments, comprehension tests and the elicitation follow up study.
5.2 Results for the bargaining-delay procedure
Our third main result is that the bargaining-delay procedure yields similar results as the other two procedures for implementing discounting. This result can be seen in Fig. 3, which shows average first-round offers and equilibrium predictions of the two treatments using the bargaining-delay procedure (B3S and B2S).
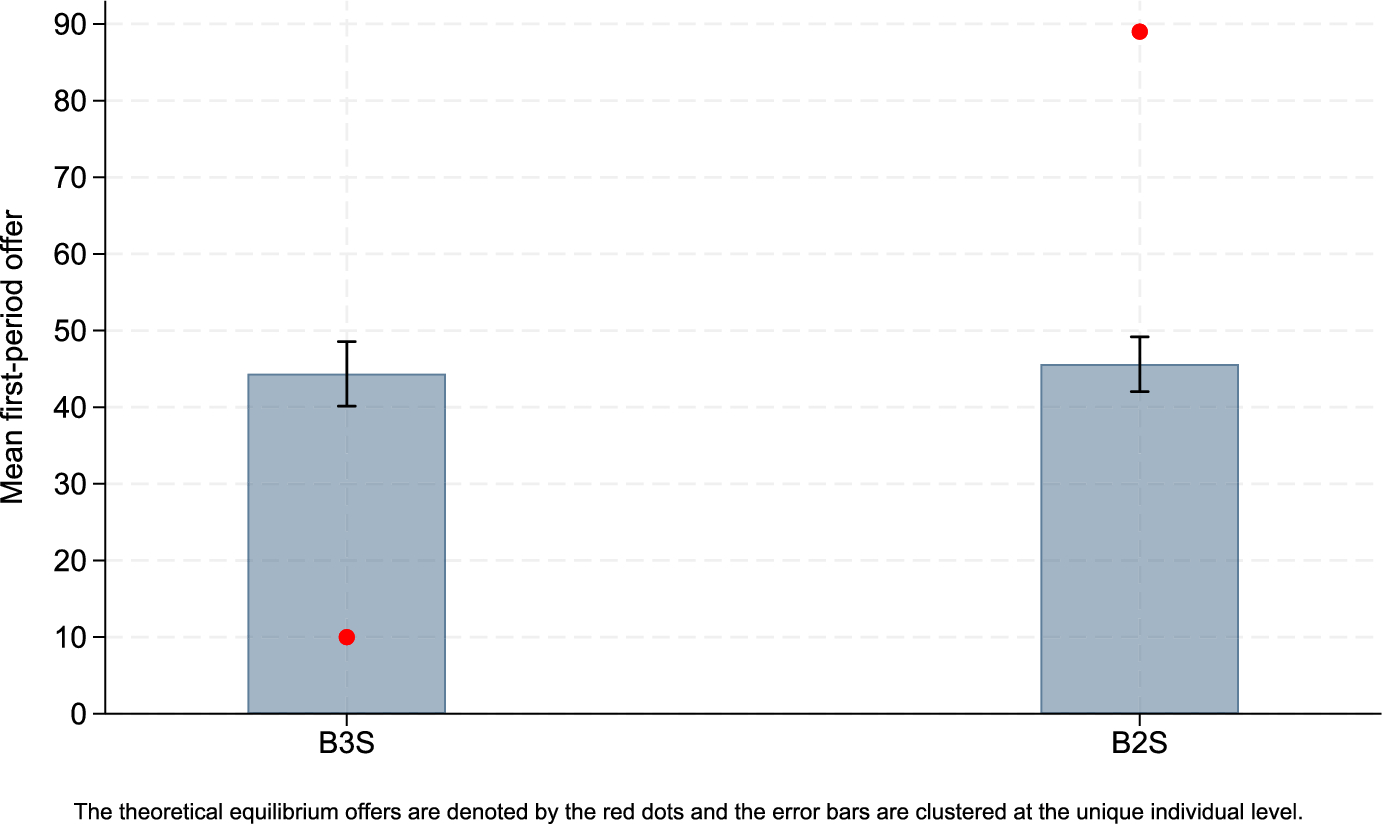
Fig. 3 Average first-period offers for B3S and B2S
We make several observations. First, as in both the shrinking-pie procedure and the effective-discounting procedure, we find no treatment effect when comparing first-period offers between the 2-period and 3-period games with the non-parametric test (
![]() = 1.000), and this is supported by all three complimentary tests (
= 1.000), and this is supported by all three complimentary tests (
![]() = 0.762;
= 0.762;
![]() = 0.729;
= 0.729;
![]() = 0.333). Second, first-period offers are 44.4 and 45.6 for B3S and B2S, respectively, which are also closer to a 50-50 split than they are to the model's predictions of 9.5 and 89.3, respectively. Third, rejection rates are in the range of.29–.36, which is similar to what was found in the effective-discounting procedure. The bargaining-delay procedure is also less efficient than the shrinking-pie procedure and is similar in efficiency to the effective-discounting procedure.
= 0.333). Second, first-period offers are 44.4 and 45.6 for B3S and B2S, respectively, which are also closer to a 50-50 split than they are to the model's predictions of 9.5 and 89.3, respectively. Third, rejection rates are in the range of.29–.36, which is similar to what was found in the effective-discounting procedure. The bargaining-delay procedure is also less efficient than the shrinking-pie procedure and is similar in efficiency to the effective-discounting procedure.
6 Conclusion
We examine whether different procedures of implementing discounting affect experimental results in a finite-time alternating-offers bargaining game. To do this examination, we analyze treatment differences of changing the number of periods or the discount factor using the shrinking-pie procedure, the effective-discounting procedure, and the bargaining-delay procedure.
We find support for the result of Ochs and Roth (Reference Ochs and Roth1989) showing that altering the number of periods does not impact behavior using any of the three procedures. Our results are less clear when altering the discount factor of the responder in two-period games; both with the shrinking-pie procedure and with the effective-discounting procedure there are significant treatment effects in two of our four empirical approaches, but the magnitudes are small. We conclude that the three different methods for implementing discounting in finite-time bargaining experiments yield similar results.
Funding
Open access funding provided by Norwegian Business School.
Data availability
The data that support the findings of this study are available on request from the corresponding author.
Declarations
Conflict of interest
The authors declare that we have no Conflict of interest.








