No CrossRef data available.
Article contents
Bias in q and m rate estimates
Published online by Cambridge University Press: 20 April 2012
Extract
Bias in estimates of the initial decremental rate q and the central decremental rate m is considered for several survival functions. It is first shown that the central rate estimate  is unbiased when the survival function is an exponential curve;
is unbiased when the survival function is an exponential curve; 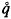 is similarly unbiased when the survival function assumes the Balducci shape. The evidence presented here also indicates that the proportional bias (the bias divided by the true value) is approximately twice as great for
is similarly unbiased when the survival function assumes the Balducci shape. The evidence presented here also indicates that the proportional bias (the bias divided by the true value) is approximately twice as great for 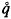 as for
as for  when the survival function is a straight line.
when the survival function is a straight line.
Life tables in common use in the United Kingdom are, however, concave at ages arising most frequently in actuarial calculations, while none of the above curves is concave. In order to investigate the bias properties of general survival functions a quadratic is chosen, with a parameter indicating the extent of curvature. For this particular class of survival functions, one can show that bias is approximately minimized when exposure to risk is symmetric about the middle of the rate year.
- Type
- Research Article
- Information
- Copyright
- Copyright © Institute and Faculty of Actuaries 1987


