Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gavin, John
Haberman, Steven
and
Verrall, Richard
1993.
Moving weighted average graduation using kernel estimation.
Insurance: Mathematics and Economics,
Vol. 12,
Issue. 2,
p.
113.
Tutz, Gerhard
and
Pritscher, Lisa
1996.
Nonparametric estimation of discrete hazard functions.
Lifetime Data Analysis,
Vol. 2,
Issue. 3,
p.
291.
Wang, Jane-Ling
Müller, Hans-Georg
and
Capra, William B.
1998.
Analysis of oldest-old mortality: lifetables revisited.
The Annals of Statistics,
Vol. 26,
Issue. 1,
Felipe, Angie
Guillen, Montserrat
and
Nielsen, Jens Perch
2001.
Longevity studies based on kernel hazard estimation.
Insurance: Mathematics and Economics,
Vol. 28,
Issue. 2,
p.
191.
Miller, Robert B.
2004.
Encyclopedia of Actuarial Science.
Peristera, Paraskevi
and
Kostaki, Anastasia
2005.
An evaluation of the performance of kernel estimators for graduating mortality data.
Journal of Population Research,
Vol. 22,
Issue. 2,
p.
185.
Wang, Jane‐Ling
2005.
Encyclopedia of Biostatistics.
Haberman, Steven
2005.
Encyclopedia of Biostatistics.
Debón, Ana
Montes, Francisco
and
Sala, Ramón
2006.
A Comparison of Nonparametric Methods in the Graduation of Mortality: Application to Data from the Valencia Region (Spain).
International Statistical Review,
Vol. 74,
Issue. 2,
p.
215.
Mazza, Angelo
and
Punzo, Antonio
2011.
New Perspectives in Statistical Modeling and Data Analysis.
p.
127.
Tomas, Julien
2012.
Essays on Boundaries Effects and Practical Considerations for Univariate Graduation of Mortality by Local Likelihood Models.
Assurances et gestion des risques,
Vol. 80,
Issue. 2,
p.
203.
Abdous, Belkacem
Kokonendji, Célestin C.
and
Senga Kiessé, Tristan
2012.
On semiparametric regression for count explanatory variables.
Journal of Statistical Planning and Inference,
Vol. 142,
Issue. 6,
p.
1537.
Mazza, Angelo
and
Punzo, Antonio
2013.
Statistical Models for Data Analysis.
p.
225.
Mazza, Angelo
and
Punzo, Antonio
2013.
Classification and Data Mining.
p.
243.
Wang, Jane‐Ling
2014.
Wiley StatsRef: Statistics Reference Online.
B. Miller, Robert
2014.
Wiley StatsRef: Statistics Reference Online.
Haberman, Steven
2014.
Wiley StatsRef: Statistics Reference Online.
Mazza, Angelo
and
Punzo, Antonio
2015.
Bivariate discrete beta Kernel graduation of mortality data.
Lifetime Data Analysis,
Vol. 21,
Issue. 3,
p.
419.
Li, Han
and
O’Hare, Colin
2017.
Semi-parametric extensions of the Cairns–Blake–Dowd model: A one-dimensional kernel smoothing approach.
Insurance: Mathematics and Economics,
Vol. 77,
Issue. ,
p.
166.
Beltrão, Kaizo Iwakami
and
Sugahara, Sonoe
2017.
Executive branch federal civil servant mortality by sex and educational level - 1993/2014.
Revista Contabilidade & Finanças,
Vol. 28,
Issue. 75,
p.
445.
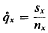
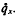 The technique has been used for smoothing data sets arising in medicine and criminology (Copas(1)(2)) and is extended here to an actuarial example and the results compared with more traditional approaches.
The technique has been used for smoothing data sets arising in medicine and criminology (Copas(1)(2)) and is extended here to an actuarial example and the results compared with more traditional approaches.

