No CrossRef data available.
Article contents
On a New Method of Constructing a Table of the Probabilities of Survivorship between Two Lives, for every Combination of Ages, and also a Table of the Present Value of Survivorship Assurances of £1 on (x) against (y)
Published online by Cambridge University Press: 18 August 2016
Extract
The present paper was undertaken on happening to peruse very lately Messrs. Gray, Smith, and Orchard's laborious and useful work, entitled Assurance and Annuity Tables, according to the Carlisle rate of Mortality, at 3 per Cent. In the introductory section of that work, when referring to the larger Tables V. and VI., containing the single and annual premiums for survivorship assurances, it is there very justly remarked, “Considering the frequency with which occasion arises for the functions here tabulated, and the tedious nature of the operations requisite when their values have to be formed from other tables, it may, at first sight, seem surprising that complete tables of them had not been formed long ere now; but the wonder will cease when it is farther considered that, until recently, there had been pointed out no other method of forming them than the tedious operation just referred to.
- Type
- Research Article
- Information
- Copyright
- Copyright © Institute and Faculty of Actuaries 1852
References
page 307 note * If we multiply the numerator and denominator of the above expression by the same quantity, or by l x+1, l y+1, its value will not be altered, though its form will be changed; thus,
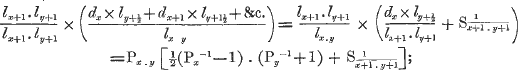
which is the expression given in Tables and Formula for the same function, ![]() found above.
found above.
page 309 note *
As the factors dx and lx+ ½ consist only offrom two to five digits their product, ![]() might perhaps be as expeditiously obtained without the intervention of logarithms, by placing those two slips together according to the difference of age, with a blank slip at the right, and a weight on the top. The factors being then opposite one another may be multiplied together on scroll paper, and the results set down on the blank slip as they are found. This table, When completed, could then be used in connection with Table XL. of Mr. Jones' work.
might perhaps be as expeditiously obtained without the intervention of logarithms, by placing those two slips together according to the difference of age, with a blank slip at the right, and a weight on the top. The factors being then opposite one another may be multiplied together on scroll paper, and the results set down on the blank slip as they are found. This table, When completed, could then be used in connection with Table XL. of Mr. Jones' work.
page 311 note * If the numerator and denominator of this fraction be multiplied by D x+1.y+1, its form will be changed into
therefore,
which is Mr. Gray's formula, as given in his Tables and Formula.
This form of expression, from its compactness, possesses more of the character of an algebraical formula than the one found above, and has been accurately and extensively exemplified by the publication of Assurance and Annuity Tables, the offspring of this new and ingenious method of construction; but it must be borne in mind that Mr. Sang's object was to adapt his formula to the commutation form, which had already worked so successfully in the computation of his Single Life Tables. It is very probable, however, from his entire acquaintance with the subject, that he was quite aware of the connection thus shown to exist between any given value and the next younger, though such a formula would evidently not suit his object.
page 313 note *
The present value of a benefit payable at death is evidently greater than a similar benefit payable six months after death. And as the payments in the former case are, on an average, made six months earlier in each year, the expression for ![]() payable at death, which we may denote by
payable at death, which we may denote by ![]() will become
will become
and this is the formula from which Mr. Sang's tables were computed. But if this fraction be multiplied by ![]() it will become
it will become
that is, ![]() or, which is the same thing,
or, which is the same thing, ![]() the assurance payable six months after death.
the assurance payable six months after death.
The same relation might be shown to subsist between Mr. Sang's single life assurance values, and the value of the same benefit due six months later. And although it is unfortunate that he made such an assumption when computing his Single Life Tables, there is not on that account such inconvenience in using them as might be supposed, where a desire is felt to obtain the smaller value. For since ![]() =0·0064186, the assurance values there tabulated may be easily converted into similar values payable six months later, by subtracting this quantity, or to suit his five place logs. 0·00642 from each column of logarithms, to which the corresponding natural numbers will be the values required: or the value for a single case may be found very nearly by dividing by 1·0149, a number easily remembered.
=0·0064186, the assurance values there tabulated may be easily converted into similar values payable six months later, by subtracting this quantity, or to suit his five place logs. 0·00642 from each column of logarithms, to which the corresponding natural numbers will be the values required: or the value for a single case may be found very nearly by dividing by 1·0149, a number easily remembered.


