No CrossRef data available.
Published online by Cambridge University Press: 18 August 2016
The application of bonus to the hastening of the time fixed by the original contract for the payment of a life assurance policy, and the using of it to extinguish the premiums payable during the latter years of life, are systems, which, partly from their growing favor with the public, and consequent adoption by many offices, and still more from the fact, that the subject is by no means exhausted, notwithstanding various able articles that have appeared in this Journal, seem to me to render apology unnecessary for again treating of it.
page 366 note * In the above formulæ, the amount of Assurance is supposed to be £1. If any other amount be wished to be employed, say S, we shall have to substitute for d+ωx; wherever it occurs, S(d+ωx).
page 369 note * Since writing the above, Mr. Ralph P. Hardy has kindly put at my service, a method he employs to find n, when one bonus only is introduced, and both policy and Endowment are valued at same rates.
In (2), divide by Dx+y, and we have
and, thus, we have the unknown member of this equation, take the form of an annuity deferred n years, of which the amount is known, as also the present age of the life. Whence n can be readily found, from a Table of such annuities.
page 371 note * It will perhaps make this clearer to say that (n) exposes the Office to an additional current risk,—that of having to pay the reversionary bonus—but (ε) exposes the Office to no such risk; and the values of the bonuses at the outset being equal, the outstanding liability of the Office, after the expiration of any assigned interval, is therefore greater in the case of (ε) than of (n).—ED. J. I. A.
page 380 note * A proof of this is hardly necessary; perhaps, however, it may be well to furnish one.
Let two assurers with any Office each pay the premium Px—the one, purchasing an Endowment Assurance payable at (x + v), without additions—the other, an ordinary assurance payable at death, with additions, the amount of this assurance being assumed the same. The latter invests these additions in endowments which became finally payable at age (x + n). Which is least, n or v?
The premium Px each pays, is made up in the following way. There is a premium ωx, which being invested at realised rates, will secure the sum contracted for, at death. This, together with the addition for expenses, and the margin from which springs the profit, makes up Px. This margin we shall call f.
In the Endowment Assurance uncertain, (we shall take for illustration the first of the two systems merely), we have seen the formula is, when all the rates are the same, i.e. the realized rates,
It must be remembered, as we there said, that these formulæ do not allow the policyholder any profit for the period from (x + Φy) to (x + n). Let ib be this profit, and as we suppose the policyholder to reap now all benefit possible, we must add ib to our formula, which will thus become
Now as f is the only source of profit, we can calculate the value of b. Thus
and substituting these values of b in the formula, we have
Again, in the Endowment assurance certain, since (x + v) is the age at which the sum assured is payable, then, at that age, for ω (the premium actually necessary to provide assurance at death) the policyholder will have enjoyed a temporary assurance of £1, and an endowment, then payable, of ![]() (that is, the surrender value of a whole life assurance); but he then receives £1, so (as ω+fis the premium, less expenses, he actually pays), f must be the premium for an endowment of
(that is, the surrender value of a whole life assurance); but he then receives £1, so (as ω+fis the premium, less expenses, he actually pays), f must be the premium for an endowment of ![]() . Whence
. Whence ![]() . Substituting this for f, in the expression given above, we have,
. Substituting this for f, in the expression given above, we have,
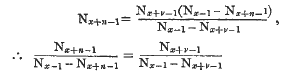
Whence, from the construction of Commutation Tables, Nx+x+1 must be equal to and therefore n = v.—Q.E.D.