Article contents
Boundary behaviour of special cohomology classes arising from the Weil representation
Published online by Cambridge University Press: 03 July 2012
Abstract
In our previous paper [J. Funke and J. Millson, Cycles with local coefficients for orthogonal groups and vector-valued Siegel modular forms, American J. Math. 128 (2006), 899–948], we established a correspondence between vector-valued holomorphic Siegel modular forms and cohomology with local coefficients for local symmetric spaces 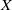 $X$ attached to real orthogonal groups of type
$X$ attached to real orthogonal groups of type 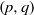 $(p, q)$. This correspondence is realized using theta functions associated with explicitly constructed ‘special’ Schwartz forms. Furthermore, the theta functions give rise to generating series of certain ‘special cycles’ in
$(p, q)$. This correspondence is realized using theta functions associated with explicitly constructed ‘special’ Schwartz forms. Furthermore, the theta functions give rise to generating series of certain ‘special cycles’ in 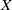 $X$ with coefficients.
$X$ with coefficients.
In this paper, we study the boundary behaviour of these theta functions in the non-compact case and show that the theta functions extend to the Borel–Sere compactification 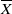 $ \overline{X} $ of
$ \overline{X} $ of 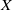 $X$. However, for the
$X$. However, for the 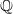 $ \mathbb{Q} $-split case for signature
$ \mathbb{Q} $-split case for signature 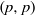 $(p, p)$, we have to construct and consider a slightly larger compactification, the ‘big’ Borel–Serre compactification. The restriction to each face of
$(p, p)$, we have to construct and consider a slightly larger compactification, the ‘big’ Borel–Serre compactification. The restriction to each face of 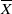 $ \overline{X} $ is again a theta series as in [J. Funke and J. Millson, loc. cit.], now for a smaller orthogonal group and a larger coefficient system.
$ \overline{X} $ is again a theta series as in [J. Funke and J. Millson, loc. cit.], now for a smaller orthogonal group and a larger coefficient system.
As an application we establish in certain cases the cohomological non-vanishing of the special (co)cycles when passing to an appropriate finite cover of 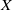 $X$. In particular, the (co)homology groups in question do not vanish. We deduce as a consequence a sharp non-vanishing theorem for
$X$. In particular, the (co)homology groups in question do not vanish. We deduce as a consequence a sharp non-vanishing theorem for 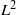 ${L}^{2} $-cohomology.
${L}^{2} $-cohomology.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 3 , July 2013 , pp. 571 - 634
- Copyright
- ©Cambridge University Press 2012
References
- 8
- Cited by

