Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T05:16:04.029Z Has data issue: false hasContentIssue false
  • English
  • Français

FUJITA DECOMPOSITION AND HODGE LOCI

Part of: Deformations of analytic structures Families, fibrations Cycles and subschemes Curves

Published online by Cambridge University Press:  12 November 2018

Paola Frediani ,
Alessandro Ghigi Open the ORCID record for Alessandro Ghigi [Opens in a new window]  and
Gian Pietro Pirola
Paola Frediani
Affiliation:
Università di PaviaItaly (paola.frediani@unipv.it; alessandro.ghigi@unipv.it; gianpietro.pirola@unipv.it)
Alessandro Ghigi
Affiliation:
Università di PaviaItaly (paola.frediani@unipv.it; alessandro.ghigi@unipv.it; gianpietro.pirola@unipv.it)
Gian Pietro Pirola
Affiliation:
Università di PaviaItaly (paola.frediani@unipv.it; alessandro.ghigi@unipv.it; gianpietro.pirola@unipv.it)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper contains two results on Hodge loci in 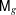$\mathsf{M}_{g}$. The first concerns fibrations over curves with a non-trivial flat part in the Fujita decomposition. If local Torelli theorem holds for the fibers and the fibration is non-trivial, an appropriate exterior power of the cohomology of the fiber admits a Hodge substructure. In the case of curves it follows that the moduli image of the fiber is contained in a proper Hodge locus. The second result deals with divisors in 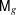$\mathsf{M}_{g}$. It is proved that the image under the period map of a divisor in 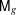$\mathsf{M}_{g}$ is not contained in a proper totally geodesic subvariety of 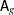$\mathsf{A}_{g}$. It follows that a Hodge locus in 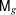$\mathsf{M}_{g}$ has codimension at least 2.

Keywords

variations of Hodge structureHodge lociFujita decomposition

MSC classification

Primary: 14C30: Transcendental methods, Hodge theory , Hodge conjecture 14D07: Variation of Hodge structures 14H10: Families, moduli (algebraic) 14H15: Families, moduli (analytic) 14H40: Jacobians, Prym varieties 32G20: Period matrices, variation of Hodge structure; degenerations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 4 , July 2020 , pp. 1389 - 1408
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors were partially supported by MIUR PRIN 2015 ‘Moduli spaces and Lie theory’ and by GNSAGA of INdAM. The first author was also partially supported by FIRB 2012 ‘Moduli Spaces and their Applications’.

References

Arbarello, E., Cornalba, M. and Griffiths, P. A., Geometry of Algebraic Curves, Vol. II, Grundlehren der Mathematischen Wissenschaften, Volume 268 (Springer, New York, 2011).Google Scholar
André, Y., Mumford–Tate groups of mixed Hodge structures and the theorem of the fixed part, Compositio Math. 82(1) (1992), 1–24.Google Scholar
Berndt, J. and Olmos, C., On the index of symmetric spaces, J. Reine Angew. Math. To appear.Google Scholar
Borel, A., Density and maximality of arithmetic subgroups, J. Reine Angew. Math. 224 (1966), 78–89.Google Scholar
Bourbaki, N., Éléments de mathématique. Fasc. XXXVIII: Groupes et algèbres de Lie. Chapitre VII: Sous-algèbres de Cartan, éléments réguliers. Chapitre VIII: Algèbres de Lie semi-simples déployées, in Actualités Scientifiques et Industrielles, No. 1364 (Hermann, Paris, 1975).Google Scholar
Carlson, J., Green, M., Griffiths, P. and Harris, J., Infinitesimal variations of Hodge structure. I, Compos. Math. 50(2–3) (1983), 109–205.Google Scholar
Catanese, F. and Dettweiler, M., The direct image of the relative dualizing sheaf needs not be semiample, C. R. Math. Acad. Sci. Paris 352(3) (2014), 241–244.Google Scholar
Catanese, F. and Dettweiler, M., Answer to a question by Fujita on Variation of Hodge Structures, in Higher Dimensional Algebraic Geometry – in Honour of Professor Yujiro Kawamata’s Sixtieth Birthday, Adv. Stud. Pure Math., 74, pp. 73–102 (Math. Soc. Japan, Tokyo, 2017).Google Scholar
Catanese, F. and Dettweiler, M., Vector bundles on curves coming from variation of Hodge structures, Internat. J. Math. 27(7) (2016), 1640001, 25.Google Scholar
Ciliberto, C. and van der Geer, G., Subvarieties of the moduli space of curves parametrizing Jacobians with nontrivial endomorphisms, Amer. J. Math. 114(3) (1992), 551–570.Google Scholar
Ciliberto, C., van der Geer, G. and Teixidor i Bigas, M., On the number of parameters of curves whose Jacobians possess nontrivial endomorphisms, J. Algebraic Geom. 1(2) (1992), 215–229.Google Scholar
Colombo, E. and Frediani, P., Some results on the second Gaussian map for curves, Michigan Math. J. 58(3) (2009), 745–758.Google Scholar
Colombo, E. and Frediani, P., Siegel metric and curvature of the moduli space of curves, Trans. Amer. Math. Soc. 362(3) (2010), 1231–1246.Google Scholar
Colombo, E., Frediani, P. and Ghigi, A., On totally geodesic submanifolds in the Jacobian locus, Internat. J. Math. 26(1) (2015), 1550005, 21.Google Scholar
Colombo, E. and Pirola, G. P., Some density results for curves with nonsimple Jacobians, Math. Ann. 288(1) (1990), 161–178.Google Scholar
Colombo, E., Pirola, G. P. and Tortora, A., Hodge-Gaussian maps, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 30(1) (2001), 125–146.Google Scholar
Deligne, P., Théorie de Hodge. II, Publ. Math. Inst. Hautes Études Sci. 40 (1971), 5–57.Google Scholar
Farb, B. and Margalit, D., A Primer on Mapping Class Groups, Princeton Mathematical Series, Volume 49 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Frediani, P., Ghigi, A. and Penegini, M., Shimura varieties in the Torelli locus via Galois coverings, Int. Math. Res. Not. IMRN (20) (2015), 10595–10623.Google Scholar
Fujita, T., The sheaf of relative canonical forms of a Kähler fiber space over a curve, Proc. Japan Acad. Ser. A Math. Sci. 54(7) (1978), 183–184.Google Scholar
Fujita., T., On Kähler fiber spaces over curves, J. Math. Soc. Japan 30(4) (1978), 779–794.Google Scholar
Fulton, W. and Harris, J., Representation Theory (Springer, New York, 1991).Google Scholar
Goodman, R. and Wallach, N. R., Symmetry, Representations, and Invariants (Springer, Dordrecht, 2009).Google Scholar
González-Alonso, V., Stoppino, L. and Torelli, S., On the rank of the flat unitary factor of the Hodge bundle, Preprint, 2017, arXiv:math/1709.05670.Google Scholar
Green, M., Griffiths, P. and Kerr, M., Mumford-Tate Groups and Domains, Annals of Mathematics Studies, Volume 183 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Kobayashi, S., Differential Geometry of Complex Vector Bundles, Publications of the Mathematical Society of Japan, Volume 15 (Princeton University Press, Princeton, NJ, 1987). Kanô Memorial Lectures, 5.Google Scholar
Kobayashi, S. and Nomizu, K., Foundations of Differential Geometry, Vol. II (Wiley, New York, London, Sydney, 1969).Google Scholar
Kollár, J., Subadditivity of the Kodaira dimension: fibers of general type, in Algebraic geometry, Sendai, 1985, Adv. Stud. Pure Math., Volume 10, pp. 361–398 (North-Holland, Amsterdam, 1987).Google Scholar
Marcucci, V., Naranjo, J. C. and Pirola, G. P., Isogenies of Jacobians, Algebr. Geom. 3(4) (2016), 424–440.Google Scholar
Moonen, B., Special subvarieties arising from families of cyclic covers of the projective line, Doc. Math. 15 (2010), 793–819.Google Scholar
Moonen, B., An Introduction to Mumford–Tate groups. https://www.math.ru.nl/∼bmoonen/Lecturenotes/MTGps.pdf.Google Scholar
Moonen, B., Linearity properties of Shimura varieties. I, J. Algebraic Geom. 7(3) (1998), 539–567.Google Scholar
Moonen, B. and Oort, F., The Torelli locus and special subvarieties, in Handbook of Moduli, Vol. II, pp. 549–594 (International Press, Boston, MA, 2013).Google Scholar
Mumford, D., A note of Shimura’s paper ‘Discontinuous groups and abelian varieties’, Math. Ann. 181 (1969), 345–351.Google Scholar
Peters, C., The local Torelli theorem. I. Complete intersections, Math. Ann. 217(1) (1975), 1–16.Google Scholar
Peters, C. A. M. and Steenbrink, J. H. M., Monodromy of Variations of Hodge Structure, Acta Appl. Math. 75 (2003), 183–194.Google Scholar
Pirola, G. P., The infinitesimal variation of the spin abelian differentials and periodic minimal surfaces, Comm. Anal. Geom. 6(3) (1998), 393–426.Google Scholar
Pirola, G. P., Base number theorem for abelian varieties. An infinitesimal approach, Math. Ann. 282(3) (1988), 361–368.Google Scholar
Pirola, G. P. and Torelli, S., Massey products and Fujita decomposition, Preprint, 2017. arXiv:math/1710.02828.Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic Groups and Number Theory (Academic Press Inc., Boston, MA, 1994).Google Scholar
Satake, I., Algebraic Structures of Symmetric Domains. Iwanami Shoten, Tokyo (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Sato, M. and Kimura, T., A Classification of Irreducible Prehomogeneous Vector Spaces and their Relative Invariants, Nagoya Math. J. 65 (1977), 1–155.Google Scholar
Schmid, W., Variation of Hodge structure: the singularities of the period mapping, Invent. Math. 22 (1973), 211–319.Google Scholar
Schnell, C., Two lectures about Mumford-Tate groups, Rend. Semin. Mat. Univ. Politec. Torino 69(2) (2011), 199–216.Google Scholar
Schoen, C., Varieties dominated by product varieties, Internat. J. Math. 7(4) (1996), 541–571.Google Scholar
Voisin, C., Hodge loci, in Handbook of Moduli, Vol. III, pp. 507–546 (Int. Press, Somerville, MA, 2013).Google Scholar
Voisin, C., Théorie de Hodge et géométrie algébrique complexe (Société Mathématique de France, Paris, 2002).Google Scholar