No CrossRef data available.
Article contents
INTÉGRALES ORBITALES SUR 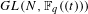 $GL(N,\mathbb{F}_{q}((t)))$
$GL(N,\mathbb{F}_{q}((t)))$
Published online by Cambridge University Press: 14 May 2019
Résumé
Soit  $F$ un corps local non archimédien de caractéristique
$F$ un corps local non archimédien de caractéristique 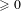 ${\geqslant}0$, et soit
${\geqslant}0$, et soit 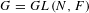 $G=GL(N,F)$,
$G=GL(N,F)$, 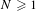 $N\geqslant 1$. Un élément
$N\geqslant 1$. Un élément 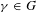 $\unicode[STIX]{x1D6FE}\in G$ est dit quasi régulier si le centralisateur de
$\unicode[STIX]{x1D6FE}\in G$ est dit quasi régulier si le centralisateur de  $\unicode[STIX]{x1D6FE}$ dans
$\unicode[STIX]{x1D6FE}$ dans 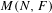 $M(N,F)$ est un produit d’extensions de
$M(N,F)$ est un produit d’extensions de  $F$. Soit
$F$. Soit 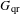 $G_{\text{qr}}$ l’ensemble des éléments quasi réguliers de
$G_{\text{qr}}$ l’ensemble des éléments quasi réguliers de  $G$. Pour
$G$. Pour 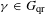 $\unicode[STIX]{x1D6FE}\in G_{\text{qr}}$, on note
$\unicode[STIX]{x1D6FE}\in G_{\text{qr}}$, on note 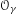 $O_{\unicode[STIX]{x1D6FE}}$ l’intégrale orbitale ordinaire sur
$O_{\unicode[STIX]{x1D6FE}}$ l’intégrale orbitale ordinaire sur 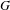 $G$ associée à
$G$ associée à  $\unicode[STIX]{x1D6FE}$. On remplace ici le discriminant de Weyl
$\unicode[STIX]{x1D6FE}$. On remplace ici le discriminant de Weyl 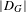 $|D_{G}|$ par un facteur de normalisation
$|D_{G}|$ par un facteur de normalisation 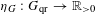 $\unicode[STIX]{x1D702}_{G}:G_{\text{qr}}\rightarrow \mathbb{R}_{{>}0}$ permettant d’obtenir les mêmes résultats que ceux prouvés par Harish-Chandra en caractéristique nulle: pour
$\unicode[STIX]{x1D702}_{G}:G_{\text{qr}}\rightarrow \mathbb{R}_{{>}0}$ permettant d’obtenir les mêmes résultats que ceux prouvés par Harish-Chandra en caractéristique nulle: pour 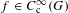 $f\in C_{\text{c}}^{\infty }(G)$, l’intégrale orbitale normalisée
$f\in C_{\text{c}}^{\infty }(G)$, l’intégrale orbitale normalisée 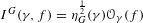 $I^{G}(\unicode[STIX]{x1D6FE},f)=\unicode[STIX]{x1D702}_{G}^{\frac{1}{2}}(\unicode[STIX]{x1D6FE})O_{\unicode[STIX]{x1D6FE}}(f)$ est bornée sur
$I^{G}(\unicode[STIX]{x1D6FE},f)=\unicode[STIX]{x1D702}_{G}^{\frac{1}{2}}(\unicode[STIX]{x1D6FE})O_{\unicode[STIX]{x1D6FE}}(f)$ est bornée sur 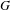 $G$, et pour
$G$, et pour 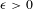 $\unicode[STIX]{x1D716}>0$ tel que
$\unicode[STIX]{x1D716}>0$ tel que 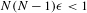 $N(N-1)\unicode[STIX]{x1D716}<1$, la fonction
$N(N-1)\unicode[STIX]{x1D716}<1$, la fonction 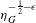 $\unicode[STIX]{x1D702}_{G}^{-\frac{1}{2}-\unicode[STIX]{x1D716}}$ est localement intégrable sur
$\unicode[STIX]{x1D702}_{G}^{-\frac{1}{2}-\unicode[STIX]{x1D716}}$ est localement intégrable sur 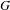 $G$.
$G$.
Abstract
Let  $F$ be a non–Archimedean local field of characteristic
$F$ be a non–Archimedean local field of characteristic 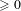 ${\geqslant}0$, and let
${\geqslant}0$, and let 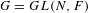 $G=GL(N,F)$,
$G=GL(N,F)$, 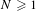 $N\geqslant 1$. An element
$N\geqslant 1$. An element 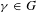 $\unicode[STIX]{x1D6FE}\in G$ is said to be quasi–regular if the centralizer of
$\unicode[STIX]{x1D6FE}\in G$ is said to be quasi–regular if the centralizer of  $\unicode[STIX]{x1D6FE}$ in
$\unicode[STIX]{x1D6FE}$ in 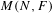 $M(N,F)$ is a product of field extensions of
$M(N,F)$ is a product of field extensions of  $F$. Let
$F$. Let 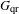 $G_{\text{qr}}$ be the set of quasi–regular elements of
$G_{\text{qr}}$ be the set of quasi–regular elements of 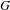 $G$. For
$G$. For 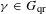 $\unicode[STIX]{x1D6FE}\in G_{\text{qr}}$, we denote by
$\unicode[STIX]{x1D6FE}\in G_{\text{qr}}$, we denote by 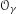 $O_{\unicode[STIX]{x1D6FE}}$ the ordinary orbital integral on
$O_{\unicode[STIX]{x1D6FE}}$ the ordinary orbital integral on 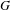 $G$ associated with
$G$ associated with  $\unicode[STIX]{x1D6FE}$. In this paper, we replace the Weyl discriminant
$\unicode[STIX]{x1D6FE}$. In this paper, we replace the Weyl discriminant 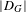 $|D_{G}|$ by a normalization factor
$|D_{G}|$ by a normalization factor 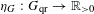 $\unicode[STIX]{x1D702}_{G}:G_{\text{qr}}\rightarrow \mathbb{R}_{{>}0}$ which allows us to obtain the same results as proven by Harish–Chandra in characteristic zero: for
$\unicode[STIX]{x1D702}_{G}:G_{\text{qr}}\rightarrow \mathbb{R}_{{>}0}$ which allows us to obtain the same results as proven by Harish–Chandra in characteristic zero: for 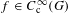 $f\in C_{\text{c}}^{\infty }(G)$, the normalized orbital integral
$f\in C_{\text{c}}^{\infty }(G)$, the normalized orbital integral 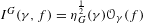 $I^{G}(\unicode[STIX]{x1D6FE},f)=\unicode[STIX]{x1D702}_{G}^{\frac{1}{2}}(\unicode[STIX]{x1D6FE})O_{\unicode[STIX]{x1D6FE}}(f)$ is bounded on
$I^{G}(\unicode[STIX]{x1D6FE},f)=\unicode[STIX]{x1D702}_{G}^{\frac{1}{2}}(\unicode[STIX]{x1D6FE})O_{\unicode[STIX]{x1D6FE}}(f)$ is bounded on 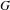 $G$, and for
$G$, and for 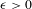 $\unicode[STIX]{x1D716}>0$ such that
$\unicode[STIX]{x1D716}>0$ such that 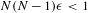 $N(N-1)\unicode[STIX]{x1D716}<1$, the function
$N(N-1)\unicode[STIX]{x1D716}<1$, the function 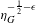 $\unicode[STIX]{x1D702}_{G}^{-\frac{1}{2}-\unicode[STIX]{x1D716}}$ is locally integrable on
$\unicode[STIX]{x1D702}_{G}^{-\frac{1}{2}-\unicode[STIX]{x1D716}}$ is locally integrable on 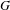 $G$.
$G$.
MSC classification
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 2 , March 2021 , pp. 423 - 515
- Copyright
- © Cambridge University Press 2019
Footnotes
L’auteur a bénéficié d’une subvention de l’Agence nationale de la recherche, projet ANR-13-BS01-00120-02 FERPLAY


