Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T21:17:32.109Z Has data issue: false hasContentIssue false
  • English
  • Français

New global stability estimates for the Calderón problem in two dimensions

Part of: Miscellaneous topics - Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  07 June 2012

Matteo Santacesaria
Matteo Santacesaria*
Affiliation:
Centre de Mathématiques Appliquées – UMR 7641, École Polytechnique, 91128, Palaiseau, France (santacesaria@cmap.polytechnique.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a new global stability estimate for the Gel’fand–Calderón inverse problem on a two-dimensional bounded domain. Specifically, the inverse boundary value problem for the equation 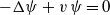${- }\Delta \psi + v\hspace{0.167em} \psi = 0$ on 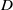$D$ is analysed, where $v$ is a smooth real-valued potential of conductivity type defined on a bounded planar domain 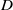$D$. The main feature of this estimate is that it shows that the smoother a potential is, the more stable its reconstruction is. Furthermore, the stability is proven to depend exponentially on the smoothness, in a sense to be made precise. The same techniques yield a similar estimate for the Calderón problem for electrical impedance tomography.

Keywords

Calderón problemelectrical impedance tomographySchrödinger equationglobal stability in 2Dgeneralized analytic functions

MSC classification

Secondary: 35R30: Inverse problems 35J15: Second-order elliptic equations
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 3 , July 2013 , pp. 553 - 569
Copyright
©Cambridge University Press 2012 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alessandrini, G., Stable determination of conductivity by boundary measurements, Appl. Anal. 27 (1) (1988), 153–172.Google Scholar
Alessandrini, G. and Vessella, S., Lipschitz stability for the inverse conductivity problem, Adv. Appl. Math. 35 (2) (2005), 207–241.Google Scholar
Astala, K. and Päivärinta, L., Calderón’s inverse conductivity problem in the plane, Ann. Math. 163 (2006), 265–299.Google Scholar
Barceló, J. A., Barceló, T. and Ruiz, A., Stability of the inverse conductivity problem in the plane for less regular conductivities, J. Differential Equations 173 (2001), 231–270.Google Scholar
Barceló, T., Faraco, D. and Ruiz, A., Stability of Calderón inverse conductivity problem in the plane, J. Math. Pures Appl. 88 (6) (2007), 522–556.Google Scholar
Beals, R. and Coifman, R. R., Multidimensional inverse scatterings and nonlinear partial differential equations, in Pseudodifferential operators and applications (Notre Dame, Ind., 1984), Proc. Sympos. Pure Math., Volume 43. pp. 45–70 (American Mathematical Society, Providence, RI, 1985).Google Scholar
Beretta, E. and Francini, E., Lipschitz stability for the electrical impedance tomography problem: the complex case, Comm. Partial Differential Equations 36 (10) (2011), 1723–1749.Google Scholar
Bukhgeim, A. L., Recovering a potential from Cauchy data in the two-dimensional case, J. Inverse Ill-Posed Probl. 16 (1) (2008), 19–33.Google Scholar
Calderón, A. P., On an inverse boundary problem, in Seminar on numerical analysis and its applications to continuum physics, pp. 61–73 (Soc. Brasiliera de Matematica, Rio de Janeiro, 1980).Google Scholar
Dubrovin, B. A., Krichever, I. M. and Novikov, S. P., The Schrödinger equation in a periodic field and Riemann surfaces, Dokl. Akad. Nauk SSSR 229 (1) (1976), 15–18.Google Scholar
Faddeev, L. D., Growing solutions of the Schrödinger equation, Dokl. Akad. Nauk SSSR 165 (3) (1965), 514–517.Google Scholar
Gel’fand, I. M., Some aspects of functional analysis and algebra, in Proceedings of the international congress of mathematicians (ed. Noordhoff, Erven P. and Groningen, N. V.). 1, pp. 253–276 (North-Holland Publishing Co., Amsterdam, 1954), Amsterdam.Google Scholar
Grinevich, P. G. and Novikov, S. P., Two-dimensional “inverse scattering problem” for negative energies and generalized-analytic functions. I. Energies below the ground state, Funct. Anal. Appl. 22 (1) (1988), 19–27.Google Scholar
Henkin, G. M. and Novikov, R. G., The $\bar {\partial } $-equation in the multidimensional inverse scattering problem, Russian Math. Surveys 42 (3) (1987), 109–180.Google Scholar
Isaev, M., Exponential instability in the Gel’fand inverse problem on the energy intervals, J. Inverse Ill-Posed Probl. 19 (3) (2011), 453–472; e-print arXiv:1012.2193.CrossRefGoogle Scholar
Kohn, R. and Vogelius, M., Determining conductivity by boundary measurements, Comm. Pure Appl. Math. 37 (3) (1984), 289–298.Google Scholar
Kohn, R. and Vogelius, M., Determining conductivity by boundary measurements. II. Interior results, Comm. Pure Appl. Math. 38 (5) (1985), 643–667.Google Scholar
Liu, L., Stability estimates for the two-dimensional inverse conductivity problem, PhD thesis, Department of Mathematics, University of Rochester, New York, (1997).Google Scholar
Mandache, N., Exponential instability in an inverse problem of the Schrödinger equation, Inverse Problems 17 (5) (2001), 1435–1444.Google Scholar
Nachman, A., Global uniqueness for a two-dimensional inverse boundary value problem, Ann. of Math. 143 (1996), 71–96.Google Scholar
Novikov, R. G., Multidimensional inverse spectral problem for the equation ${- }\Delta \psi + (v(x)- Eu(x))\psi = 0$, Funktsional. Anal. i Prilozhen 22 (4) (1988), 11–22 (in Russian); English Transl.: Funct. Anal. Appl. 22(4), (1988) 263–272.Google Scholar
Novikov, R. G., The inverse scattering problem on a fixed energy level for the two-dimensional Schrödinger operator, J. Funct. Anal. 103 (2) (1992), 409–463.Google Scholar
Novikov, R. G., Approximate solution of the inverse problem of quantum scattering theory with fixed energy in dimension 2, (Russian), Tr. Mat. Inst. Steklova 225 (1999), Solitony Geom. Topol. na Perekrest., 301–318; translation in Proc. Steklov Inst. Math. 225(2) (1999), 285–302.Google Scholar
Novikov, R. G., Formulae and equations for finding scattering data from the Dirichlet-to-Neumann map with non-zero background potential, Inverse Problems 21 (1) (2005), 257–270.Google Scholar
Novikov, R. G., New global stability estimates for the Gel’fand–Calderon inverse problem, Inverse Problems 27 (1) (2011), 015001.Google Scholar
Novikov, R. G. and Novikova, N. N., On stable determination of potential by boundary measurements, ESAIM Proc. 26 (2009), 94–99.Google Scholar
Novikov, R. G. and Santacesaria, M., A global stability estimate for the Gel’fand–Calderón inverse problem in two dimensions, J. Inverse Ill-Posed Probl. 18 (7) (2010), 765–785.Google Scholar
Sylvester, J. and Uhlmann, G., A global uniqueness theorem for an inverse boundary value problem, Ann. of Math. 125 (1) (1987), 153–169.Google Scholar
Vekua, I. N., Generalized analytic functions. (Pergamon Press Ltd., 1962).Google Scholar